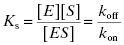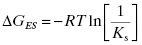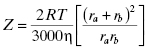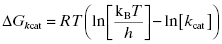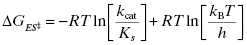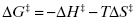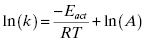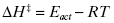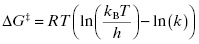The binary complex ES is commonly referred to as the ES complex, the initial encounter complex, or the Michaelis complex. As described above, formation of the ES complex represents a thermodynamic equilibrium, and is hence quantifiable in terms of an equilibrium dissociation constant, Kd, or in the specific case of an enzyme–substrate complex, KS, which is defined as the ratio of reactant and product concentrations, and also by the ratio of the rate constants koff and kon (see Appendix 2):
The equilibrium dissociation constant KS has units of molarity and its value is inversely proportional to the affinity of the substrate for the enzyme (i.e., the lower the value of KS, the higher the affinity). The value of KS can be readily converted to a thermodynamic free energy value by the use of the familiar Gibbs free energy equation:
where R is the ideal gas constant and T is temperature in degrees Kelvin (note that for use in Equation 2.2 the value of KS is expressed as molar, not μM nor nM). Similar thermodynamic relationships hold for the reversible interactions of inhibitors with enzymes, as will be described in Chapter 3.
Thus, as described by Equation (2.1), the equilibrium dissociation constant depends on the rate of encounter between the enzyme and substrate and on the rate of dissociation of the binary ES complex.
According to collision theory, there are three factors that limit the rate of bimolecular encounters: the frequency of collisional events (Z); a steric factor (ρ), which takes into account that only a fraction of collisional events will occur with both molecules properly oriented relative to one another for reaction; and the activation energy of reaction (Eact or ΔG‡). The rate of productive encounters is thus given by the following equations:
(2.3) 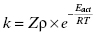
and
where ra and rb are the molecular radii of the two colliding molecules, a and b, and η is the viscosity of the medium in which the reaction is taking place. The maximum rate of reaction would occur when Eact is zero and all encounters occur with both molecules properly oriented for reaction (i.e., ρ = 1). Thus the maximum rate is given by Z (Equation 2.4). This rate reflects the encounter frequency of the two molecules and is referred to as the diffusion controlled rate. For a low molecular weight ligand and a protein target, the diffusion limit on association (i.e., kon) has been calculated to be in the range of 1 × 109 M−1s−1 (Fersht, 1999). Similarly, the upper limit for the dissociation rate of a bimolecular complex (i.e., koff) has been determined to be between 109 and 1012 s−1. These extreme rates, however, are not seen in experimental measures of protein-ligand complex association and dissociation, largely because of the influence of steric parameters and activation energies (vide supra) as well as a significant impact of conformational dynamics of the macromolecular target on reaction (see Chapters 6 and 8).
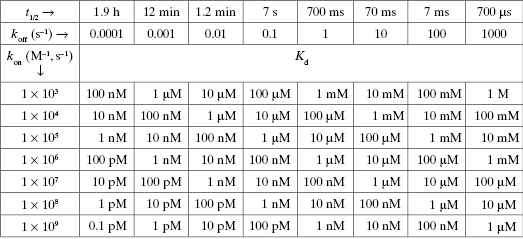
Table 2.1 illustrates how the combination of these two rate constants can influence the overall value of Kd (in general) for any equilibrium binding process. One may think that association between the enzyme and substrate (or other ligands) is exclusively rate-limited by collisional encounters. However, as described above and further in Chapters 6 and 8, this is not always the case. Sometimes conformational adjustments of the enzyme’s active site must occur prior to productive ligand binding, and these conformational adjustments may occur on a time scale slower that diffusion. Likewise the rate of dissociation of the ES complex back to the free reactant state can vary significantly from one enzyme to another. This dissociation process is counterproductive to catalysis, as it competes with the forward process of bound substrate transformation to products.
2.2 Noncovalent Forces in Reversible Ligand Binding to Enzymes
As we have just seen, the initial encounter complex between an enzyme and its substrate is characterized by a reversible equilibrium between the binary complex and the free forms of enzyme and substrate. Hence the binary complex is stabilized through a variety of noncovalent interactions between the substrate and enzyme molecules. Likewise the majority of pharmacologically relevant enzyme inhibitors, which we will encounter in subsequent chapters, bind to their enzyme targets through a combination of noncovalent interactions. Some of the more important of these noncovalent forces for interactions between proteins (e.g., enzymes) and ligands (e.g., substrates, cofactors, and reversible inhibitors) include electrostatic interactions, hydrogen bonds, hydrophobic forces, and van der Waals forces (Copeland, 2000).
2.2.1 Electrostatic Forces
If two molecules of opposing electrostatic charge are brought into close proximity a Coulombic force of attraction is created. This attractive force is directly proportional to the charges on the two molecules, is inversely proportional to the square of the distance between the two molecules, and is inversely proportional to the dielectric constant of the intervening medium (Copeland, 2000). Electrostatic interactions occur between charged groups within ligand molecules and complementary charges within the enzyme binding pocket, in the form of dipole–dipole interactions, salt bridges, metal chelation effects, and general ion pairing. Because the strength of these interactions is inversely proportional to the dielectric constant of the medium, these forces are strengthened significantly in the low dielectric environment of a protein binding pocket, relative to what is observed in aqueous solution. Hence electrostatic interactions can provide an important thermodynamic driving force for ligand binding to proteins. Active site metal chelation, dipolar interactions, charge neutralization, and other forms of electrostatic functionalities can often be designed into inhibitor molecules to gain binding energy through interactions with specific, complementary functionalities within an enzyme’s binding pocket. In subsequent chapters we will encounter a number of examples of this.
2.2.2 Hydrogen Bonds
Hydrogen bonding involves the sharing of a proton between two electronegative atoms. The proton is covalently bonded to one electronegative atom, which is referred to as the hydrogen bond donor; the other electronegative atom involved in the hydrogen bond is referred to as the hydrogen bond acceptor. Both donor and acceptor atoms are almost exclusively heteratoms; in proteins hydrogen bond donors and acceptors are mainly nitrogen and oxygen atoms, and sometime sulfur atoms.
The strength of an individual hydrogen bond is directly proportional to the linear distance between the heteroatoms acting as donor and acceptor. In proteins, typical hydrogen bond lengths range from 2.7 to 3.1 Å, and this translates into relatively weak forces, with hydrogen bond strengths of around 1 to 5 kcal/mol (although some unusually strong hydrogen bonds have been reported in enzyme systems; e.g., see Cleland and Kreewoy, 1994). However, multiple hydrogen bonds can occur between an enzyme’s binding pocket and a ligand so that the cumulative effect of these hydrogen bonds imparts a significant stabilizing force for the enzyme–ligand binary complex.
2.2.3 Hydrophobic Forces
Dissolution of a nonpolar molecule into a polar solvent, such as water, is energetically costly. If a more nonpolar solvent is mixed into the sample, the nonpolar molecule will spontaneously partition into the more nonpolar solvent. In a like manner, nonpolar molecules will partition into the hydrophobic environment of an enzyme’s binding pocket, and this can impart a favorable stabilizing energy to the enzyme–ligand binary complex. Enzyme active sites are generally hydrophobic but often contain highly polarized groups as part of their catalytic machinery. Designing hydrophobic portions of a substrate or inhibitor molecule to make favorable interactions with the nonpolar components of the active site, while avoiding unfavorable contacts with the more highly polarized components of the pocket, can enhance binding affinity significantly. In the absence of structural information on the binding pocket of the specific target enzyme, it is difficult to predict quantitatively the contribution to the free energy of binding that hydrophobic interactions may have. However, the overall hydrophobicity of a ligand molecule can be quantified in terms of its free energy for partitioning between water and the nonpolar solvent octanol. If one dissolves a molecule into an equal volume mixture of water and octanol, the molecule will partition between the two solvents over time. At equilibrium one can measure the concentration of the molecule in each solvent and define a partition ratio, P, as the ratio of the molecule concentration in octanol over its concentration in water. The logarithm of P is then directly proportional to the free energy of partitioning, and is used as a relative measure of compound hydrophobicity. Ligands, especially drug molecules, that interact with enzymes in vivo generally display log(P) values between 2 and 5 (Lipinski et al., 1997). This range of log(P), however, reflects not only target enzyme affinity but other factors (oral absorption, cell permeability, etc.) that are important for in vivo efficacy of a drug molecule, and that are affected by hydrophobicity. The exact relationship between log(P) and enzyme binding affinity will depend on the structural details of the enzyme active site. For chymotrypsin, for example, Fersht reports that the log(kcat/KM) for peptide substrate utilization (kcat/KM is a relative measure of enzyme efficiency, as will be defined later in this chapter) increases linearly with the value of log(P). Likewise the binding affinity of a series of substituted formanilide inhibitors of chymotrypsin was linearly dependent on log(P) as well. Hence for ligands of the chymotrypsin active site, greater hydrophobicity translates into greater binding affinity (Fersht, 1999).
2.2.4 Van der Waals Forces
Fluctuations in the electron cloud around an atomic nucleus can create asymmetric distributions of charge that result in a transient dipole moment. This dipole moment can affect the electron cloud of a nearby atom to create an attractive force between the two atoms, known as a van der Waals bond. Although weak in energy, large numbers of these interactions can occur when there is good steric and electrostatic complementarity between the binding pocket on the enzyme and the structure of the ligand bound within the pocket. The potential energy of interaction for van der Waals bonds is very sensitive to the distance between electron clouds of the interacting atoms. At too far a distance, the dipole moment induced in one electron cloud cannot impact the electron cloud of the distal atom. If the two atoms approach too closely, the electron clouds will repulse each other. Hence the optimum contact distance for van der Waals interactions depends on the identity of the two atoms involved. For each atom there will be a characteristic van der Waals radius that defines the closest contact distance attainable for a partnering atom’s electron cloud. Characteristic van der Waals radii for different atoms are well defined for the atoms contained within enzymes and their ligands. These can be found in numerous texts, including Copeland (2000).
2.3 Transformations of the Bound Substrate
Once the initial encounter complex is formed, the bound substrate must be acted upon by the chemically reactive components of the enzyme active site to transform the substrate to product(s). This typically occurs via the formation of a series of intermediate species in which active site components interact with specific portions of the substrate to distort bond lengths and angles in a way that directs the substrate structure toward the transition state of the chemical reaction and from there on to the product state. As with any chemical reaction, it is formation of the transition state that represents the greatest thermodynamic barrier to reaction progress and also typically represents the most rate-limiting chemical step in the reaction pathway (Copeland, 2000). In fact the key to rate acceleration in enzyme catalysis is the reduction of the energy barrier (i.e., activation energy) for attainment of the reaction transition state (Pauling, 1948). For our example case of a simple single substrate enzyme reaction, we may have multiple intermediate states along the reaction pathway between the ES complex and the final state of free enzyme and product(s) molecules. At minimum we must occupy a state representing the bound transition state of the substrate (ES‡) and a state representing the bound product (EP). Each of these states is connected to its antecedent and subsequent state by a set of micro-reversible equilibria:
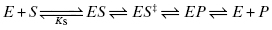
In practice, measurement of the individual rate constants or equilibrium constants for these various chemical steps requires specialized methodologies, such as transient state kinetics (see Johnson, 1992; Copeland, 2000; and Fersht, 1999 for discussion of such methods) and/or a variety of biophysical methods for measuring equilibrium binding (Copeland, 2000). These specialized methods are beyond the scope of the present text. More commonly, the overall rate of reaction progress after ES complex formation is quantified experimentally in terms of a composite rate constant given the symbol kcat.
Although kcat is a composite rate constant, representing multiple chemical steps in catalysis, it is dominated by the rate-limiting chemical step, which most often is the formation of the bound transition state complex ES‡ from the encounter complex ES. Thus, to a first approximation, we can consider kcat to be a first-order rate constant for the transition from ES to ES‡
The Gibbs free energy for the transition from ES to ES‡ is related to the value of kcat as described by Equation (2.5):
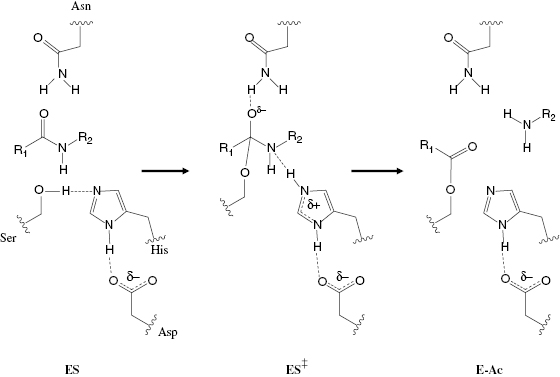
where kB is the Boltzmann constant and h is Planck’s constant. Combining Equations (2.2) and (2.5) yields an equation for the overall free energy change for the transition from the free reactant state (E + S) to the bound transition state (ES‡) and thus represents the overall activation energy for the enzyme-catalyzed reaction:
From Equation (2.6) we see that the overall activation energy for the enzyme-catalyzed reaction is related to the second-order rate constant defined by the ratio kcat/KS.
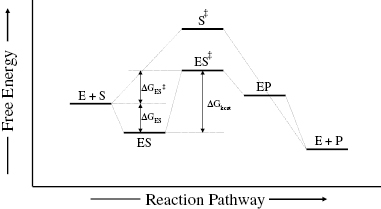
Figure 2.1 summarizes these energy relationships in terms of the free energy changes that accompany progress through the various states of the reaction pathway. Also shown in Figure 2.1 is the free energy diagram for the cognate chemical reaction in the absence of enzyme catalysis. The most striking difference between the two energy diagrams is the significant lowering of the activation energy (i.e., the vertical distance between the reactant state and the transition state) in the case of the enzyme-catalyzed reaction. In other words, the transition state is greatly stabilized in the enzyme catalyzed reaction relative to the noncatalyzed reaction, and this is the entire basis of enzymatic reaction rate enhancement.
Figure 2.1 Free energy diagram for the reaction pathway of a chemical reaction, and the same reaction catalyzed by an enzyme. Note the significant reduction in activation energy (the vertical distance between the reactant state and the transition state) achieved by the enzyme-catalyzed reaction.
2.3.1 Strategies for Transition State Stabilization
The structural and chemical mechanisms used by enzymes to achieve transition state stabilization have been reviewed in detail elsewhere (e.g., see Jencks, 1969; Warshel, 1998; Cannon and Benkovic, 1998; Copeland, 2000; Copeland and Anderson, 2002; and Kraut et al., 2003). Four of the most common strategies used by enzymes for transition state stabilization—approximation, covalent catalysis, acid/base catalysis, and conformational distortion—are discussed below.
Approximation
Approximation refers to the bringing together of the substrate molecules and reactive functionalities of the enzyme active site into the required proximity and orientation for rapid reaction. Consider the reaction of two molecules, A and B, to form a covalent product A–B. For this reaction to occur in solution, the two molecules would need to encounter each other through diffusion-controlled collisions. The rate of collision is dependent on the temperature of the solution and molar concentrations of reactants. The physiological conditions that support human life, however, do not allow for significant variations in temperature or molarity of substrates. For a collision to lead to bond formation, the two molecules would need to encounter one another in a precise orientation to effect the molecular orbitial distortions necessary for transition state attainment. The chemical reaction would also require at least partial desolvation of each molecule, and this would impose an additional energy cost to reaction in solution. On the other hand, binding of molecules A and B to the enzyme active site significantly diminishes these barriers to reaction. Simply by binding to the enzyme, the two molecules will come into close proximity with one another. This dramatically increases the local concentration of each substrate, within the restricted volume of the enzyme active site, thus greatly enhancing the probability of productive interactions. The specificity of interactions between each molecule and particular components of the enzyme active site that stabilize the ES complex would ensure appropriate molecular orbital alignment of A and B to facilitate the bond distortions required to reach the reaction transition state. The cost of desolvation of A and B is no longer a barrier to reaction in the enzyme-bound state, as this cost was already offset by the favorable binding energy associated with formation of the ES complex. Finally there is an entropic advantage to bond formation between substrates A and B in the enzyme active site, relative to the reaction in solution. By forming a covalent bond between the two molecules, the overall number of rotational and translational degrees of freedom are reduced. The activation energy for reaction is composed of both enthalpic and entropic terms, as is any free energy term:
Hence the reduction in entropy (ΔS‡) that results from loss of rotational and translational freedom leads to a more positive (unfavorable) value of ΔG‡. The enthaplic and entropic components of ΔGkcat and ΔGES‡ can be determined from the temperature dependence of kcat and of kcat/KS, respectively, from the Arrhenius equation
The term A in Equation (2.6) is a constant known as the Arrhenius constant and Eact is the energy of activation derived from collision theory (Atkins, 1978). The enthalpy of activation can be calculated from transition state theory (Jencks, 1969) as
And the Gibbs free energy change of activation is given by the Eyring equation:
Knowing the values of ΔG‡ and ΔH‡ from Equations (2.10) and (2.9), one can calculate TΔS‡ from Equation (2.7) (Mittelstaedt and Schimerlik, 1986). In this way Bruice and Benkovic (1965) calculated the value of TΔS‡ for a diverse group of 40 chemical reactions in solution, and found that the average cost of losing one set of translational and rotational degrees of freedom due to bond formation was about 4.7 kcal/mol (19.8 kJ/mol). When, however, the substrates A and B are brought together in the enzyme active site, the loss of translational and rotational degrees of freedom is paid for in the binding step, so it no longer contributes unfavorably to the energy of activation. Thus, at minimum, the activation energy in the enzyme catalyzed reaction is reduced by about 4.7 kcal/mol, which translates into an approximately 3000-fold enhancement of the reaction rate.
The collective set of energetic advantages that result from productive substrate binding to the enzyme active site is known as the approximation effect. In concert, these effects can provide an important means of at least partially lowering the activation energy for transition state formation.
Covalent Catalysis
Enzymes can promote bond distortions by forming covalent bonds between active site functionalities and appropriate groups on the substrate molecule. The covalent intermediates that result from such bond formation tend to bring the substrate molecule into closer steric and electronic resemblance with the reaction transition state. Thus the system overcomes a significant part of the energy barrier to transition state attainment. Later in the reaction pathway the covalent bond formed between the enzyme and substrate is cleaved so that products may leave the enzyme active site and thus return the enzyme molecule to its original state. Covalent catalysis is most often mediated by interactions between enzyme active site nucelophiles and corresponding electrophilic centers on substrate molecules (nucleophilc catalysis), or by enzyme active-site electrophiles interacting with substrate nucleophiles (electrophilic catalysis). Serine proteases, for example, use nucleophilic catalysis to catalyze amide bond cleavage in substrate peptides and proteins (Copeland, 2000). The nucleophilicity of the side chain hydroxyl group of an active-site serine is significantly augmented by spacially precise hydrogen bonding between the serine side chain and the side chains of active-site histidine and aspartate residues. Formation of the initial, noncovalent ES encounter complex is followed by nucleophilic attack of the scissile amide bond by the active-site serine residue, leading to covalent bond formation between the serine oxygen and the carbonyl carbon of the amide (Figure 2.2). This creates a covalent transition state-like species, containing an oxyanionic tetrahedral carbon center. This is charge-stabilized by hydrogen bonding with an active-site asparagine side chain. Proton donation from the active site histidine to the substrate amide nitrogen leads to rupture of the substrate C–N bond, and dissociation of the amine-containing product (H2N–R2). This leaves behind an acyl intermediate consisting of the carbonyl product (R1–COO) of the amide bond cleavage reaction that is still covalently attached to the active-site serine oxygen atom. Subsequent binding of a water molecule to the active site leads to hydrolysis of the acyl intermediate, dissociation of the second product, and return of the enzyme to its original state. Copeland and Anderson (2001) and Silverman (1992) have presented several additional examples of both nucleophilic and electrophilic covalent catalysis.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree