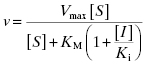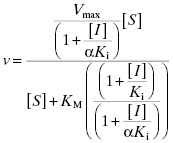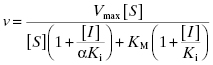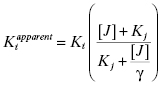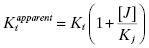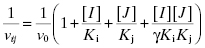3.1 Enzyme–Inhibitor Binding Equilibria
As we have seen before, the enzymatic reaction begins with the reversible binding of substrate (S) to the free enzyme (E) to form the ES complex, as quantified by the dissociation constant KS. The ES complex thus formed goes on to generate the reaction product(s) through a series of chemical steps that are collectively defined by the first-order rate constant kcat. The first mode of inhibitor interaction that can be considered is one in which the inhibitor binds to the free enzyme, in direct competition with the substrate. The equilibrium between the binary EI complex and the free enzyme and inhibitor molecules is defined by the dissociation constant Ki. The EI complex thus formed could bind the substrate to form a ternary ESI complex. However, the affinity of the EI complex for substrate may not be the same as that for the free enzyme. Hence the dissociation constant KS must be modified by the constant α to describe substrate binding to the EI complex. The constant α defines the degree to which inhibitor binding affects the affinity of the enzyme for substrate. If there is no change in substrate affinity due to formation of the EI complex, then α = 1. If formation of the EI complex excludes the further binding of substrate, then α = ∞. Finally, if formation of the EI complex augments the affinity of the enzyme for substrate, α < 1.
Alternatively, the ESI complex can be formed by binding of inhibitor to the preformed ES complex. Because this represents a thermodynamic cycle, the value of Ki in this case is modified by the same constant α as was the value of KS. It is possible for the ESI complex to then go on to produce product, albeit at a reduced rate relative to the uninhibited reaction (Segel, 1975; Copeland, 2000). This situation is referred to as partial inhibition, and there are examples of drugs in clinical use that work by such a mechanism (e.g., the nonnucleoside HIV reverse transcriptase inhibitors used in the treatment of AIDS are thought to function as partial inhibitors; Spence et al., 1995). Thus at saturating concentrations these drugs do not abolish the activity of their target enzyme, but instead sufficiently diminish the rate of catalysis to produce the desired therapeutic effect. While some examples of partial inhibitors are known, the majority of therapeutically useful enzyme inhibitors function by completely abrogating enzyme activity at saturating concentrations. Compounds of this type are referred to as dead-end inhibitors, and these will be the focus of the remainder of this chapter.
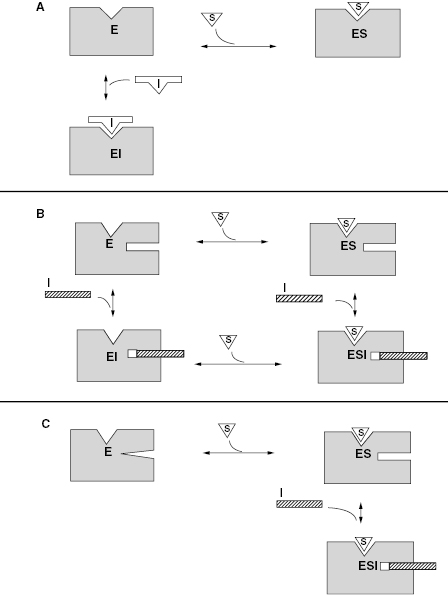
Hence, according to the equilibria in Figure 3.1, Ki represents the equilibrium dissociation constant for the EI complex and αKi represents the equilibrium dissociation constant for the ESI complex1 (or for enzyme–inhibitor complexes whose formation is dependent on the prior formation of the ES complex, see below). We can thus define three potential modes of inhibitor interactions with enzymes based on the equilibria in Figure 3.1: competitive inhibitors that bind exclusively to the free enzyme form, noncompetitive inhibitors that bind with some affinity to both the free enzyme and to the ES complex (or subsequent species in the reaction pathway), and uncompetitive inhibitors that bind exclusively to the ES complex or subsequent species. Figure 3.2 depicts these different inhibition modalities in cartoon form (Copeland, 2000). In the sections to follow we will describe these three inhibition modalities in more detail.
Figure 3.2 Cartoon representations of the three major forms of reversible inhibitor interactions with enzymes: (A) competitive inhibition; (B) noncompetitive inhibition; (C) uncompetitive inhibition.
Source: From Copeland (2000).
3.2 Competitive Inhibition
An inhibitor that binds exclusively to the free enzyme (i.e., for which α = ∞) is said to be competitive because the binding of the inhibitor and the substrate to the enzyme are mutually exclusive; hence these inhibitors compete with the substrate for the pool of free enzyme molecules. Referring back to the relationships between the steady state kinetic constants and the steps in catalysis (Figure 2.8), one would expect inhibitors that conform to this mechanism to affect the apparent value of KM (which relates to formation of the enzyme–substrate complex) and Vmax/KM, but not the value of Vmax (which relates to the chemical steps subsequent to ES complex formation). The presence of a competitive inhibitor thus influences the steady state velocity equation as described by Equation (3.1):
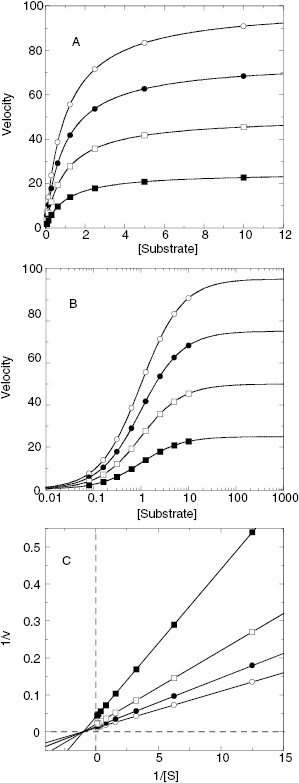
If we were to plot the velocity as a function of substrate at varying concentrations of a competitive inhibitor, we would obtain graphs such as those shown in Figure 3.3A through 3.3C. The value of Vmax is constant at all inhibitor concentrations, but the apparent value of KM (defined as KM(1 + [I]/Ki)) increases with increasing inhibitor concentration. This is apparent in the semilog plot (Figure 3.3B) where the plateau value at high substrate (Vmax) remains unchanged, but the midpoint of the S-shaped titration curve (i.e., apparent KM) shifts to the right (i.e., toward higher substrate concentration) with increasing inhibitor. The effects are perhaps most apparent in the double reciprocal plot (Figure 3.3C) where the intercept value (i.e., 1/Vmax) is constant but the slope (KM/Vmax) and x-intercept (−1/KM) values of the line change with inhibitor concentration. Thus a double reciprocal plot composed of a nest of lines that intersect at the y-axis is diagnostic of competitive inhibition (Table 3.1).
Figure 3.3 Substrate titration of steady state velocity for an enzyme in the presence of a competitive inhibitor at varying concentrations. (A) Untransformed data; (B) data as in (A) plotted on a semilog scale; (C) data as in (A) plotted in double reciprocal form. For all three plots the data are fit to Equation (3.1).
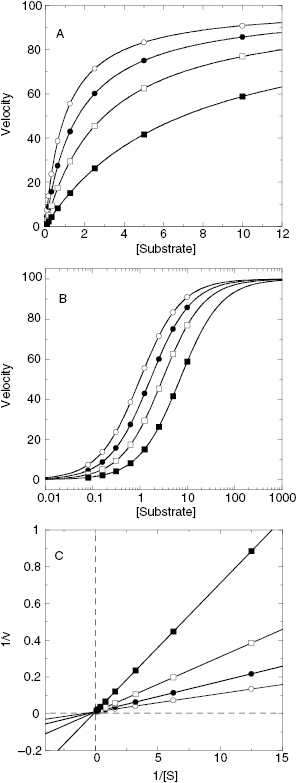
TABLE 3.1 Diagnostic Signatures of Reversible Inhibition Modalities in Double Reciprocal Plots
| Inhibition Modality | Diagnostic Signature |
|---|---|
| Competitive | Intersecting lines that converge at the y-axis |
| Noncompetitive, α > 1 | Intersecting lines that converge to the left of the y-axis and above the x-axis |
| Noncompetitive, α = 1 | Intersecting lines that converge to the left of the y-axis and on the x-axis |
| Noncompetitive, α < 1 | Intersecting lines that converge to the left of the y-axis and below the x-axis |
| Uncompetitive | Parallel lines |
Because competitive inhibitors bind to the free enzyme to the exclusion of substrate binding, it is easy to assume that this results from a direct competition of the two ligands (substrate and inhibitor) for a common binding pocket (i.e., the active site) on the enzyme molecule. While this is very often the case, it is not a mechanistic necessity. Inhibitor and substrate could bind to separate sites on the enzyme molecule that somehow exert a negative regulation on one another (i.e., through negative allosteric interactions, driven by ligand-induced conformational changes). This type of negative regulation via allosteric communication between separate binding sites on a protein is well represented in biology, especially in metabolic pathways in the form of feedback regulation (e.g., Perutz, 1990).
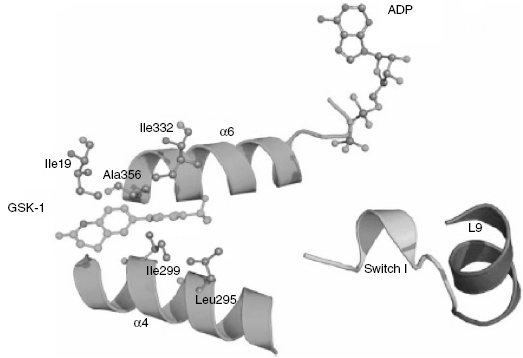
Competitive enzyme inhibits that bind at allosteric locations have also been identified. For example, Luo et al. (2007) reported a series of biaryl compounds that were potent, selective inhibitors of the mitotic kinesin KSP. Steady state analysis demonstrated that the compounds were competitive inhibitors with respect to the substrate ATP, and uncompetitive with respect to the protein substrate microtubules (MT). Crystal structures of the KSP-ADP complex were known, but the conformationally heterogeneous nature of the MT substrate precluded crystallization of the KSP-MT complex. Because the biaryl inhibitors were uncompetitive with respect to MT, crystallographic verification of the binding site for these inhibitors was a major challenge. As an alternative, Luo et al. (2007) synthesized an analogue of one of the potent biaryl compounds with a photolabile phenyltrifluoromethyldiazirine moiety. Photolysis of this compound bound to the KSP-MT binary complex led to covalent cross-linking of the compound to the protein. These workers were able to separate the KSP and MT proteins and then subject the isolated KSP to tryptic digestion and mass spectral analysis of the resulting peptides. In this way, the site of covalent attachment of the inhibitor was determined to be Leu 295, a residue distant from the known ATP/ADP binding pocket of the enzyme. In separate cellular experiments, mutations of KSP at I299F and A356T were found to confer resistance to inhibition by the biaryl compounds. The three residues, Leu 295, I299, and A 356, cluster within a common pocket in the three dimensional structure of KSP that sits at the interface of two alpha helical segments of the protein, helix 4 and helix 6 (Figure 3.4). Helix 6 connect this interfacial binding pocket directly with the distal ATP/ADP binding pocket. Thus, biaryl inhibitor binding at the helix 4/helix 6 interface results in movement of helix 6 that allosterically modifies the ATP/ADP binding pocket in such a way as to block ATP binding. In this manner, the biaryl compounds act as competitive inhibitors with respect to ATP while binding to a site on the protein that is quite distant from the ATP/ADP binding pocket.
Figure 3.4 Modeled structure of human KSP with ADP bound at one site and the allosteric, ATP-competitive inhibitor GSK-1 bound at the interface between helices 4 and 6. Note that the binding of GSK-1 at the helix interface causes a concerted movement of helix 6, resulting in changes to the ATP/ADP binding pocket.
Source: Adapted from Luo et al. (2007).
Thus one cannot assume that because an inhibitor displays the kinetic signature of a competitive inhibitor that it necessarily binds to the enzyme active site. This caveat being said, it nevertheless turns out that most of the small molecule, competitive enzyme inhibitors that are in clinical use today have been independently demonstrated (usually through X-ray crystallography) to bind within the active site of their target enzyme.
There are a very large number of drugs in clinical use today that function as competitive enzyme inhibitors; some representative examples are presented in Table 3.2. While today many drug-seeking efforts are initiated with high-throughput screens of large compound libraries (see Chapter 4), many of the drugs listed in Table 3.2 were instead identified by the complementary approaches of mechanism-based and structure-based drug design (Navia and Murcko, 1992; Wlodawer and Vondrasek, 1998). Mechanism-based drug design refers to efforts to design competitive inhibitors of enzymes based on knowledge of the catalytic reaction mechanism, using substrate, transition state, or product state mimics as starting points in the design effort (Copeland and Anderson, 2002). A good example of this strategy comes from the discoveries of the anti-hypertension drugs captopril and enalapril.
TABLE 3.2 Some Examples of Competitive Enzyme Inhibitors in Clinical Use
| Drug | Enzyme Target | Disease Indication |
|---|---|---|
| Lovastatin, Pravastatin, other statins | HMG-CoA reductase | Cholesterol lowering |
| Captopril, enalapril | Angiotensin converting enzyme | Hypertension |
| Saquinavir, indinavir, ritonavir | HIV protease | AIDSa |
| Acetazolamide | Carbonic anhydrase | Glaucoma |
| Viagra, Levitra | Phosphodiesterase | Erectile dysfunction |
| Gleevec | Bcr-Abl kinase | Cancer |
| Methotrexateb | Dihydrofolate reductase | Cancer, bacterial infection |
a Acquired immune deficiency syndrome.
b Methotrexate is competitive with respect to the substrate dihydrofolate (see Section 3.5).
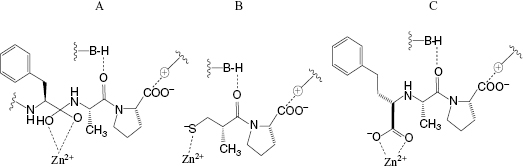
The angiotensin converting enzyme (ACE) is a zinc carboxypeptidase that catalyzes the hydrolysis of the decapeptide angiotension I to the the octapeptide angiotensin II. Angiotensin II increases blood pressure by acting as a vasoconstrictor and also by stimulating the release of aldosterone, which leads to pro-hypertensive electrolytic changes (Copeland and Anderson, 2002). ACE activity further contributes to hypertension by inactivating the vasodialating peptide bradykinin through hydrolysis. Hence inhibition of ACE leads to blood pressure lowering by blocking formation of the pro-hypertensive peptide angiotensin II and stabilizing the anti-hypertensive peptide bradykinin. Like other zinc carboxypeptidases the reaction mechanism of ACE involves formation of a coordinate bond between the carbonyl oxygen of the scissile peptide bond and the active site zinc atom. Coordinate bond formation polarizes the carbonyl bond of the peptide, thus increasing its susceptibility to nucleophilic attack by an active site-bound water molecule. This nucleophilic attack leads to a transition state containing a dioxo tetrahedral carbon center in the substrate peptide. The bound transition state is also stabilized through other active site interactions, as illustrated in Figure 3.5A. Early studies demonstrated that peptides from the venoms of South American and Japanese vipers could effectively block bradykinin and angiotensin I hydrolysis by inhibition of ACE. Separation of the peptides in these venoms identified the most potent inhibitors as small peptides (containing 5–9 amino acids) containing C-terminal proline residues. It was also known that N-acylated tripeptides are well utilized as substrates by ACE, making it reasonable to expect that small molecular weight inhibitors could be developed for this enzyme. It was subsequently found that a small molecule, (R)-2-benzylsuccinic acid, served as an effective ACE inhibitor (Silverman, 1992). Using this information as a starting point, scientists at Squibb and at Merck began systematic studies to identify small molecule inhibitors of ACE that function through the same types of active site interactions. These efforts led to two anti-hypertensive drugs, captopril (Figure 3.5B) and enalapril (a pro-drug that is converted to the active species enalaprilate, illustrated in Figure 3.5C). As illustrated in Figure 3.5, both captopril and enalaprilate function as competitive inhibitors of ACE, forming coordinate bonds with the active site zinc atom, and also forming favorable interactions with other groups within the active site of the enzyme. These interactions lead to high-affinity binding of both drugs to their target enzyme; captopril displays a Ki for human ACE of 1.7 nM (Ondetti and Cushman, 1984), while enalaprilate displays even greater affinity with a Ki of 0.18 nM (Patchett et al., 1980).
Figure 3.5 Interactions of (A) substrate, (B) captopril, and (C) enalaprilate with the active site of angiotensin converting enzyme.
Structure-based drug design refers to the systematic use of structural information about the enzyme active site (typically from X-ray crystal structures, NMR structures, or homology models based on the structures of related proteins) to design small molecules with steric and electronic features that would lead to high-affinity interactions with active site components of the target enzyme. Having solved the crystal structure of a target enzyme to atomic resolution, it is possible to evaluate the structural details of the active site and to then begin to design de novo compounds that would fit into the active site. There are many examples of inhibitors that have been designed exclusively by this de novo, structure-based method (e.g., see Navia and Murcko, 1992).
By any method, optimization of compound interactions with a binding pocket is an iterative process, requiring multiple rounds of compound evaluation, new synthesis, and further evaluation. Often, during this iterative process, one finds that the malleability inherent to enzyme active sites can present some surprises to the medicinal chemist and structural biologists. Enzyme structures can change in response to ligand binding, sometimes molding themselves to make better contacts with the ligand (e.g., see Chapters 1 and 8). In other cases the orientation of the ligand and details of specific interactions with the active site can change during the process of compound optimization. Hence the original structure of the free enzyme active site may no longer be an adequate template for understanding the structure-activity relationship (SAR) for a series of structurally related inhibitors.
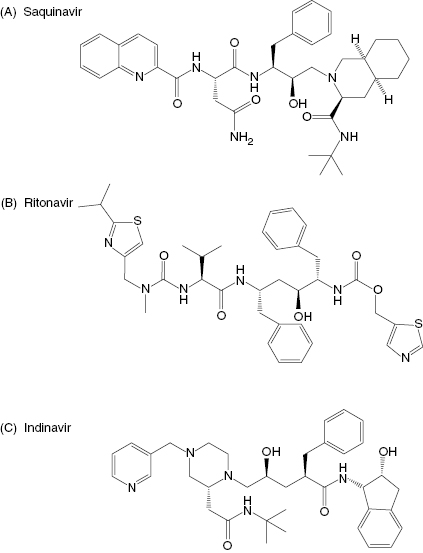
More commonly, one begins with lead compounds that are obtained from library screening or from a mechanism-based approach, and then uses the structural data to refine and optimize the interactions of compounds with the enzyme active site. Perhaps initially one would attempt to dock the lead inhibitor structure into the active site of the free enzyme through computer modeling methods. As described above, however, the flexibility of the enzyme active site limits the ultimate utility of such an approach. To use structure-based lead optimization to greatest effect, one will eventually need to generate crystal structures of individual enzyme–inhibitor complexes, and correlate the structural data thus obtained with inhibition data generated by quantitative evaluation from enzyme activity assays (Copeland, 2000). This combined approach has proved successful for a large number of drug-seeking efforts. For example, the development of inhibitors of the HIV aspartyl protease was largely driven by a combination of mechanism-based and structure-based drug design. Initial leads were generated by consideration of known peptidic substrates of the enzyme and of known transition state mimics of aspartyl proteases (statines, hydroxyethylenes, etc.). Inserting a statine or hydroxyethylene group into a peptidic substrate, at the site of the scissile amide bond, produced potent inhibitors of the viral protease. These were good starting points for inhibitor design, but were clearly too peptidic in nature to have good pharmacological properties. Significant progress in the design of HIV protease inhibitors began with the report of the crystal structure of the enzyme by Navia and coworkers (Navia et al., 1989). This opened a floodgate for the type of iterative, structure-based inhibitor design described above, with hundreds of enzyme–inhibitor complex crystal structures being solved. These efforts eventually led to the development of several HIV protease inhibitors, such as saquinavir, ritonavir, and indinavir (Figure 3.6), that are today used in the treatment of AIDS. Similar efforts are underway today at many pharmaceutical companies and academic laboratories to identify and optimize inhibitors of other enzymes of therapeutic interest.
Figure 3.6 Chemical structures of the HIV protease inhibitors: (A) saquinavir, (B) ritonavir, and (C) indinavir.
3.3 Noncompetitive Inhibition
A noncompetitive inhibitor is one that displays binding affinity for both the free enzyme and the enzyme–substrate complex or subsequent species. In this situation the binding affinity cannot be defined by a single equilibrium dissociation constant; instead, we must define two dissociation constants, one for the binary enzyme–inhibitor complex (Ki) and one for the ternary ESI complex (αKi). When the constant α is unity, the inhibitor displays equal affinity for both the free enzyme and the ES complex. When α > 1, the inhibitor preferentially binds to the free enzyme, and when α < 1, the inhibitor binds with greater affinity to the ES complex or subsequent species. There is some confusion in the literature due to different uses of the term noncompetitive inhibition. Some authors reserve this term only for the situation in which α = 1, and the affinity of the inhibitor for the free enzyme and ES complex are therefore equivalent. These authors use the term mixed-type inhibition for any situation in which α ≠ 1. In my experience, the term mixed-type inhibition can lead to misunderstandings about the physical meaning of the term (e.g., I have had discussions with chemists who have mistakenly believed that mixed-type inhibition must require two inhibitor molecules binding to separate sites on the enzyme); therefore we will use the term noncompetitive inhibition in its broader definition to describe any inhibitor that displays affinity for both the free enzyme and the ES complex.
Because noncompetitive inhibitors bind to both the free enzyme and the ES complex, or subsequent species in the reaction pathway, we would expect these molecules to exert a kinetic effect on the E + S → ES‡ process, thus affecting the apparent values of both Vmax/KM (influenced by both the Ki and αKi terms) and Vmax (influenced by the αKi term). This is reflected in the velocity equation for noncompetitive inhibition:
This equation can be simplified by multiplying the numerator and denominator by the term (1 + ([I]/αKi)) to yield
The equation can be simplified further in the specific case where the inhibitor displays equal affinity for both enzyme forms (i.e., where α = 1, therefore Ki = αKi):
(3.4) 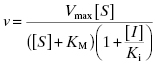
Referring back to Equation (3.2), we see that the effect of a noncompetitive inhibitor on the kinetic constants is to lower the apparent value of Vmax and to increase, decrease, or leave unaffected the apparent value of KM, depending on whether α is >1, <1 or =1, respectively (see Table 3.3 and Figure 3.7). These effects are apparent in plots of velocity as a function of substrate concentration at varying concentrations of noncompetitive inhibitors (Figure 3.8). In Figure 3.8C we see that the double reciprocal plot for noncompetitive inhibitors display a nest of lines that intersect at a point other than the y-axis. This is a diagnostic signature of noncompetitive inhibition. The plot in Figure 3.8C was generated for an inhibitor with α = 1, for which the nest of line converge at the x-axis. When α > 1, the lines intersect above the x-axis of a double reciprocal plot, and when α < 1, the lines intersect below the x-axis.
TABLE 3.3 Effects of Inhibitors of Different Modalities on the Apparent Values of Steady State Kinetic Constants and on Specific Steps in Catalysis
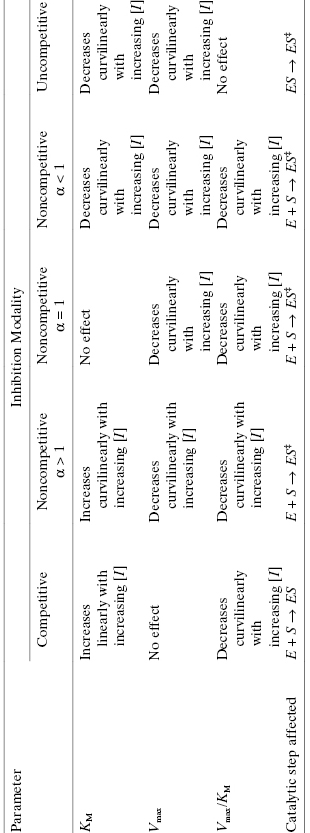
Figure 3.7 Plots of the effect of inhibitor concentration on the apparent values of Vmax (A), KM (B), and Vmax/KM (C) for competitive (circles), noncompetitive (α = 1, squares), and uncompetitive (triangles) modes of inhibition.
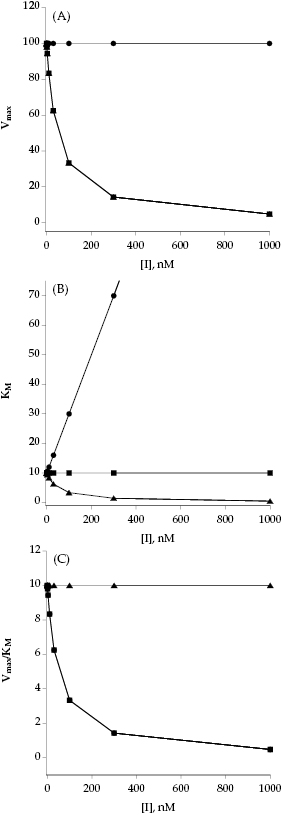
Figure 3.8 Substrate titration of steady state velocity for an enzyme in the presence of a noncompetitive inhibitor (α = 1) at varying concentrations. (A) Untransformed data; (B) data as in (A) plotted on a semilog scale; (C) data as in (A) plotted in double reciprocal form. For all three plots the data are fit to Equation (3.2).
Relative to competitive inhibitors, there are fewer examples of noncompetitive inhibitors in clinical use as drugs today. This reflects the historic approaches to drug discovery that have been largely focused on active-site directed inhibitors. With a greater emphasis on compound library screening as a mechanism of lead identification, more examples of noncompetitive inhibitors are likely to emerge, especially if attention is paid to designing screening assays that balance the opportunities for identifying the greatest diversity of inhibitor modalities (see Chapter 4). Table 3.4 lists a few examples of drugs in clinical use, or in clinical trials, that act as noncompetitive enzyme inhibitors.
TABLE 3.4 Some Examples of Noncompetitive Enzyme Inhibitors in Clinical Use or Trials
| Drug/Candidate | Enzyme Target | Disease Indication |
|---|---|---|
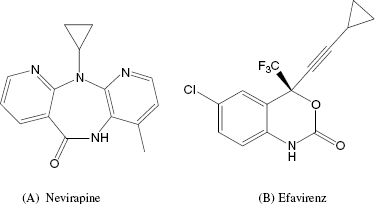
| Nevirapine, efavirenz | HIV reverse transcriptase | AIDS |
| SB-715992 | KSP kinesin | Cancer |
| PD0325901, CI-1040 | MAP kinase kinase (MEK) | Cancer |
| TF-505 | Steroid 5α-reductase | Benign prostate Hyperplasia |
| Etoposide | Topoisomerase II | Cancer |
| Tacrine | Acetylcholinesterase | Cognition (in Alzheimer’s disease) |
| Trazodone | Adenosine deaminasea | Depression |
a It is not clear that inhibition of adenosine deaminase is the basis for the clinical efficacy of Trazodone for the treatment of depression.
The nonnucleoside reverse transcriptase inhibitors (NNRTIs), used in the treatment of AIDS, provide interesting examples of clinically relevant noncompetitive inhibitors. The causative agent of AIDS, HIV, belongs to a virus family that relies on an RNA-based genetic system. Replication of the virus requires reverse transcription of the viral genomic RNA into DNA, which is then incorporated into the genome of the infected host cell. Reverse transcription is catalyzed by a virally encoded nucleic acid polymerase, known as reverse transcriptase (RT). This enzyme is critical for viral replication; inhibition of HIV RT is therefore an effective mechanism for abrogating infection in patients.
HIV RT is a heterodimer composed of two protein subunits, p51 and p66, that fold to form a classical polymerase structure. The three-dimensional structure of the enzyme contains three subdomains that are arranged in a shape resembling a human hand, so that the three subdomains are referred to as the fingers, palm, and thumb subdomains (Figure 3.9). Reverse transcription by the enzyme involves binding of an RNA or DNA template that defines the sequences of deoxynucleotide triphosphate (dNTPs; e.g., ATP, TTP, GTP, and CTP) incorporation into a small DNA primer strand. The RNA/DNA template and the DNA primer form a complex that binds to one site on the enzyme. The dNTPs bind separately to the enzyme and are then catalytically added to the primer sequence; the identity of the dNTP that is used in any particular primer extension reaction is dictated by the complementary base on the RNA/DNA template. Hence the enzyme can be considered to utilize a bisubstrate reaction mechanism, with one substrate being the template–primer complex, and the second substrate being the individual dNTP used for a specific turnover event. The kinetic mechanism has been found to be ordered, with the template–primer complex (TP) binding first, followed by dNTP binding:
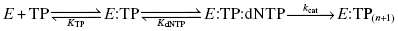
Figure 3.9 Structure of the HIV reverse transcriptase illustrating the location of the NNRTI binding pocket.
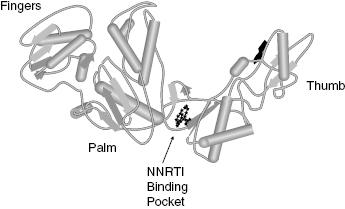
Unlike other enzymes that we have discussed, the completion of a catalytic cycle of primer extension does not result in release of the product (TP( n+1)) and recovery of the free enzyme. Instead, the product remains bound to the enzyme, in the form of a new template–primer complex, and this acts as a new substrate for continued primer extension. Catalysis continues in this way until the entire template sequence has been complemented. The overall rate of reaction is limited by the chemical steps composing kcat; these include the chemical step of phosphodiester bond formation and requisite conformational changes in the enzyme structure. Hence there are several potential mechanisms for inhibiting the reaction of HIV RT. Competitive inhibitors could be prepared that would block binding of either the dNTPs or the TP. Alternatively, noncompetitive compounds could be prepared that function to block the chemistry of bond formation, that block the required enzyme conformational transition(s) of turnover, or that alter the reaction pathway in a manner that alters the rate-limiting step of turnover.
The first inhibitors of HIV RT to be used in the clinic were structural analogues of nucleosides that acted as competitive inhibitors of dNTP binding. The main drawback of these inhibitors was a lack of selectivity for the viral enzyme over human nucleoside-utilizing enzymes, hence a limited therapeutic index. In response to the toxicity associated with nucleoside-based inhibitors of HIV RT, several companies launched library screens against the enzyme. These efforts resulted in the identification of a class of noncompetitive inhibitors known as the NNRTIs. Nevirapine and efavirenz (Figure 3.10) are two examples of NNRTIs that have proved very useful in the treatment of AIDS patients. Both compounds are highly selective for the HIV RT over human nucleoside-utilizing enzymes, due to the fact that they do not bind to the structurally common dNTP binding pocket, but instead bind to a unique binding pocket on the viral enzyme. Because of this, these compounds do not display the same toxicities associated with nucleoside-based HIV RT inhibitors.
Nevirapine inhibits HIV RT with a Ki of between 19 and 400 nM, depending on the composition of the TP complex and other assay conditions. The compound displays essentially equal affinity for the free enzyme (E), the binary E : TP and the ternary E : TP : dNTP complexes. Efavirenz also displays noncompetitive inhibition of HIV RT, but this compound demonstrates preferential binding to the E : TP : dNTP ternary complex, with Ki values for the E, E : TP, and E : TP : dNTP species of 170, 30, and 4 nM, respectively. Both nevirapine and efavirenz have been shown to bind to an allosteric pocket on the p66 subunit of the enzyme, close to the interface of the palm and thumb subdomains (Figure 3.9). Both compounds bind to the pocket largely through hydrophobic interactions; however, the compounds must interact in unique ways with the enzyme, as the effects of mutations within the binding pocket are quite different for the two drugs. For example, a common clinical isolate of HIV RT has Lys 103 mutated to Asn. Lys 103 makes van der Waals interactions with nevirapine, and the mutation of Lys103Asn results in a 40-fold increase in the Ki for this compound. In contrast, the same mutation causes only a 6-fold change in affinity for efavirenz. Crystallographic studies suggest that the Lys103Asn mutation causes important topographical changes in the NNRTI binding pocket. It appears that efavirenz can adopt a binding configuration that is less sensitive than nevirapine to the structural changes that attend mutation of Lys 103.
Unlike competitive inhibitors, noncompetitive inhibition cannot be overcome by high concentrations of substrate. This can be a significant advantage for noncompetitive inhibitors in vivo when the physiological context exposes the enzyme to high substrate concentrations. It is worth noting that this advantage for noncompetitive inhibition is not restricted to enzyme targets. Christopoulos (2002) has recently presented a review of the many examples of allosteric (i.e., noncompetitive) receptor antagonists that are used as drugs in human medicine. Because they do not compete with the natural agonist of the receptor target, these allosteric receptor antagonists offer the same advantages as drugs as do noncompetitive enzyme inhibitors.
The example of the NNRTIs described above, illustrates an additional potential advantage of noncompetitive inhibition. When compounds bind to a unique allosteric site, rather than at the catalytic active site, they can achieve high selectivity against other enzymes that utilize the same substrate or reaction mechanism as the target enzyme. Thus the NNRTIs enjoy the clinical advantage of reduced toxicity because the binding pocket to which they bind is unique to HIV RT among the many nucleoside-utilizing enzymes of the virus and human host. As described further below, however, it is often difficult to know what inhibition modality will be most effective in vivo under pathophysiological conditions. Hence all potential modes of inhibiting a target enzyme should be considered and evaluated fully.
3.3.1 Mutual Exclusivity Studies
In our example of NNRTIs we noted that there was crystallographic evidence that showed that the distinct chemical series exemplified by nevirapine and efavirenz both share a common binding pocket on the target enzyme. Early in a drug discovery effort, one may encounter a situation where there are multiple lead pharmacophores that conform to a common inhibition modality. In the absence of any crystallographic or other structural information on the enzyme–inhibitor complexes, the question of whether two pharamacophores share a common binding pocket (i.e., bind in an orthosteric manner) often arises, especially when the two compounds are both noncompetitive inhibitors (although the same issue can arise for competitive and uncompetitive inhibitors as well). Short of a high-resolution structure of the enzyme–inhibitor complexes, it is very difficult to answer this question definitively. There are, however, a number of ways that one can address whether or not the two compounds bind to the enzyme target in a mutually exclusive fashion, in other words, whether or not the two compounds are competitive with one another for binding to the enzyme. As we described above for competition between substrate and competitive inhibitors, mutually exclusive binding does not necessarily indicate a common binding pocket but is generally viewed as consistent with the possibility of a shared binding site.
If one of the compounds of interest has a unique spectroscopic feature, or can be synthesized with a fluorescent or radioactive label, then a variety of equilibrium binding studies can be performed to measure the ability of one compound to interfere with binding of a second compound to the enzyme (Copeland, 2000). By any of a number of biophysical methods, one can determine the Kd for binding of one compound (compound I; Kd of I = Ki) to the enzyme, and then look at how the apparent Kd value for that compound is affected by increasing concentrations of the second compound (compound J; Kd of J = Kj). A general equation describing the effect of compound J concentration on the apparent Kd of compound I is given by the following:
where γ is an interaction constant that determines the degree of cooperative or anticooperative binding between compounds I and J. The values of Ki and Kj are determined independently through binding experiments in the absence of the alternative compound. If the binding of I and J are mutually exclusive, then the value of γ is infinity, in which case Equation (3.5) reduces to the following (Kenakin, 1997):
Equation (3.6) is a linear equation for which a plot of 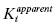 as a function of [J]/Kj will yield an ascending straight line (Figure 3.11). When γ = 1, the binding of one compound is unaffected by the binding of the second compound and one observes simple additive binding. Here a plot of
as a function of [J]/Kj will yield an ascending straight line (Figure 3.11). When γ = 1, the binding of one compound is unaffected by the binding of the second compound and one observes simple additive binding. Here a plot of 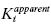 as a function of [J]/Kj will be a horizontal line. When γ > 1 < ∞, one observes antagonistic binding where the binding of one compound diminishes the affinity of the enzyme for the other compound. In this case a replot of
as a function of [J]/Kj will be a horizontal line. When γ > 1 < ∞, one observes antagonistic binding where the binding of one compound diminishes the affinity of the enzyme for the other compound. In this case a replot of 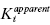 as a function of [J]/Kj will yield ascending, curvilinear relationship, as depicted in Figure 3.11. When γ < 1, one observes synergistic binding where the binding of one compound enhances the affinity of the enzyme for the other compound. In this situation the replot of
as a function of [J]/Kj will yield ascending, curvilinear relationship, as depicted in Figure 3.11. When γ < 1, one observes synergistic binding where the binding of one compound enhances the affinity of the enzyme for the other compound. In this situation the replot of 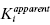 as a function of [J]/Kj will result in a descending curvilinear relationship (not shown).
as a function of [J]/Kj will result in a descending curvilinear relationship (not shown).
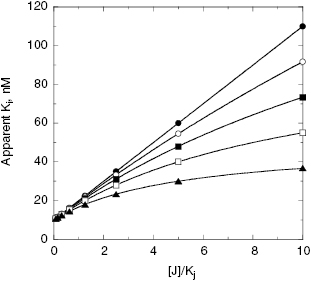
Figure 3.11 Apparent value of the dissociation constant (Ki) for a labeled inhibitor, I, as a function of the concentration of a second inhibitor, J when measured by equilibrium binding methods. The solid circles represent the behavior expected when compounds I and J bind in a mutually exclusive fashion with one another. The other symbols represent the behavior expected when compounds I and J bind in a nonexclusive, but antagonistic (i.e., noncompetitive, α > 1) fashion, to separate binding sites. The data for mutually exclusive binding were fit to the equation (apparent)Ki = Ki{1 + ([J]/Kj)} and that for nonexclusive binding were fit to the equation (apparent)Ki = Ki({[J] + Kj}/{Kj + ([J]/γ)]}) for γ values of 5 (closed triangles), 10 (open squares), 20 (closed squares), and 50 (open circles).
The observant reader will recognize that we have already encountered the above, general treatment for two ligands binding to a common enzyme in the specific case of substrate and reversible inhibitor binding. Thus, the situation described above when γ = ∞ is the equivalent of competitive inhibition with respect to substrate. Likewise, γ = 1 is the equivalent of noncompetitive inhibition, and γ << 1 would be the equivalent of uncompetitive inhibition (vide infra).
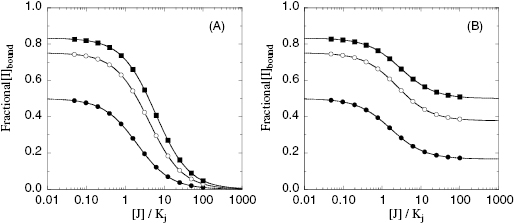
Additionally, if the two compounds bind in a mutually exclusive fashion, saturating concentrations of the second compound should be able to completely abrogate binding of the labeled first compound; thus the bound concentration of labeled compound I goes to zero (Figure 3.12A). If, instead, the two compounds are not mutually exclusive, one should be able to form a ternary complex, E : I : J, at high concentrations of the second compound. The amount of labeled I that is bound to the enzyme at any point in a titration of compound J will be due to the sum of the concentrations of E : I binary complex and of E : I : J ternary complex. Hence, instead of driving the concentration of bound label (I) to zero, one will reach a plateau of bound I that is representative of the concentration of ternary complex. In experiments of this type, the concentration of E and of labeled I are fixed to give a specific concentration of E : I complex, and this is then titrated with varying concentrations of compound J. If the concentration of E : I complex is varied, the concentration of E : I : J ternary complex that may be formed will also vary, leading to different plateau values for the titration, as illustrated in Figure 3.12B. This type of analysis was used by Favata et al. (1998) to demonstrate that two noncompetitive inhibitors of the kinase MEK (U0126 and PD098059) bound to their common enzyme target in a mutually exclusive fashion.
Figure 3.12 Concentration of labeled compound I bound to an enzyme as a function of the concentration of a second inhibitor J. (A) Response of bound I to concentration of J when I and J bind in a mutually exclusive fashion. Note that here the concentration of the bound I is driven to zero at high concentrations of J. (B) Response of bound I to concentration of J when the two compounds bind in a nonexclusive, antagonistic manner to the target enzyme. Note that at high concentrations of J one does not drive the concentration of bound I to zero. Rather, the concentration of bound I at high concentrations of J reflects the concentration of ternary E : I : J complex. Condition of simulations: [I]/Ki = 1 (closed circles), 3 (open circles), and 5 (closed squares). For panel B, γ = 5.
Mutual exclusivity can also be tested for by the effects of combinations of two inhibitors on the activity of a target enzyme. The advantage of this approach is that it does not require any special labeling of either compound, and only catalytic quantities of enzyme are required for the studies. There are a number of graphical methods that can be used to determine the effects of inhibitor combinations on enzyme velocity (see Copeland, 2000). The most popular of these was introduced by Yonetani and Theorell (1964) and is based on the following reciprocal equation:
Here vij is the enzyme velocity in the presence of both compounds at concentrations [I] and [J]. The term γ is an interaction term that defines the degree to which binding of one compound perturbs the affinity of the enzyme for the second compound.
If two compounds bind in a mutually exclusive fashion, then their effects on enzyme velocity are additive and the value of γ is infinite (i.e., the combination term in Equation 3.7 is zero). This type of analysis was used, for example, by Lai et al. (2002) to demonstrate that three distinct classes of noncompetitive inhibitors of the enzyme hdm2 all bound in a mutually exclusive fashion to the enzyme. While these data do not allow one to unambiguously conclude that the compounds share a common binding pocket on the enzyme, the data are consistent with such a hypothesis.
If two compounds bind completely independently of one another, then γ = 1. If instead the two compounds bind to the enzyme nonexclusively, but influence the affinity of each other, then γ will have a finite value. If the binding of one compound reduces the affinity of the enzyme for the second compound, the two compounds demonstrate antagonistic binding and γ > 1. A finite, but large, value of γ can indicate that the two compounds bind to the same site on the enzyme, but that this site binds the two compounds in different conformational states (Yonetani and Theorell, 1964). For example, Marcinkeviciene et al. (2002) found that pepstatin A and a substituted piperidine both displayed competitive inhibition of the aspartyl protease pepsin. Mutual exclusivity studies by the method of Yonetanii and Theorell yielded a value of γ of 8 for these two inhibitors. This was interpreted, along with other experimental results, as evidence that the two compounds bound to different conformational states of the enzyme active site that were populated at different points in the reaction pathway. If the value of γ < 1, the binding of one compound augments the affinity of the enzyme for the second compounds, and the binding of the two compounds is said to be synergistic.
To determine the value of γ, Yonetani and Theorell suggest measuring reaction velocity at several fixed concentrations of one inhibitor while titrating the second inhibitor. The reciprocal of velocity (1/vij) is then plotted as a function of concentration for the titrated inhibitor (Figure 3.13). If the two compounds are binding in a mutually exclusive fashion, this type of plot results in a series of parallel lines (Figure 3.13A). If the two compounds bind independently (γ = 1) the lines in the Yonetani-Theorell plot will converge at the x-axis. When γ is finite but not unity, the lines intersect above or below the x-axis. For any Yonetani-Theorell plot that displays intersecting lines, the x-axis value (i.e., [J]) that corresponds to the point of intersection will yield the value of −γKj. If Kj and Ki have been determined independently, one can easily calculate the value of γ from the point of intersection in a Yonetani-Theorell plot.
Figure 3.13 Yonetani-Theorell plots for determining mutual exclusivity of two inhibitors. (A) Plot for two inhibitors that bind in a mutually exclusive fashion to a target enzyme; (B) plot for two inhibitors that bind independently (γ = 1) to the same target enzyme.
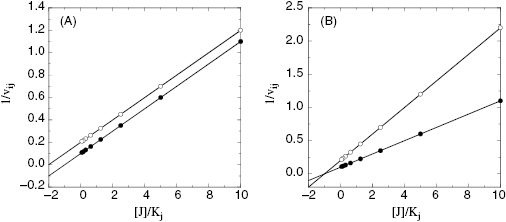
Yonetani-Theorell analysis can be quite useful in determining whether chemically distinct noncompetitive inhibitors are likely to share a common binding pocket on a target enzyme. This information can be very valuable in defining strategies for parallel SAR studies on two or more chemical series of inhibitiors.
3.3.2 Noncompetitive Inhibition by Active Site-Directed Inhibitors
In our discussion of competitive inhibitors (Section 3.2) we made the point that the steady state designation of competitive with substrate should not be taken as prima facia evidence of a common binding pocket for the substrate and the inhibitor. Although it is often the case that a competitive inhibitor binds at the substrate binding pocket (i.e., the enzyme active site), this is not always true. In a like manner, finding an inhibitor to be noncompetitive with substrate does not preclude the possibility of that compound binding at the enzyme active site. There are several mechanisms by which a compound that is bound within the enzyme active site may appear to be noncompetitive with substrate when analyzed by steady state kinetics; some these mechanisms are summarized below and have been reviewed recently by Blat (2010).
One mechanism by which an active site-directed inhibitor may appear noncompetitive with substrate is in the context of an isoenzyme mechanism of catalysis. An isoenzyme mechanism refers to a catalytic cycle that involves distinct active site conformations for the substrate binding state and the enzyme–product state of the enzyme. If interconversion between these states is slow on the time scale of catalysis, then it is possible for the free enzyme to exist in two distinct conformations: one that binds substrate and a second that reflects the conformation immediately after product release. An inhibitor that binds to the active site only in the product-release conformation would not compete for the same enzyme species that binds the substrate (Figure 3.14A). Hence, although the inhibitor and substrate would share a common binding pocket in this scenario, the two ligands would not compete with one another for binding. This type of behavior has been observed for inhibitors of aspartyl proteases (see Chapter 1), carbonic anhydrase and fumarase (see Blat, 2010, and references therein).
Figure 3.14 Some mechanisms by which an active site-directed inhibitor can behave noncompetitively with respect to the substrate of the enzymatic reaction. (A) An isoenzyme mechanism for which the inhibitor binds to a conformational state of the free enzyme that is distinct from the conformation that binds substrate. (B) An induced-fit, 2-step binding mechanism as described further in Chapters 6 and 8. (C) An enzyme that acts on a macromolecular substrate (e.g., a protein substrate) for which the binding energy is distributed across a wide surface area beyond the enzyme active site interactions. See Blat (2010) for additional examples and details.
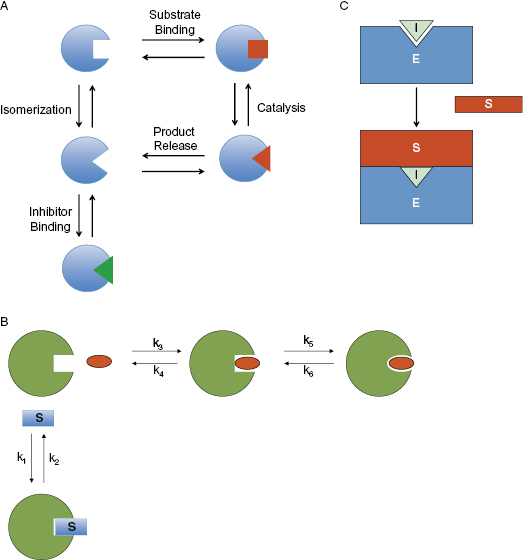
A second situation that can result in noncompetitive inhibition by active site-directed inhibitors is when the binding of inhibitor occurs through a two-step mechanism. This topic will be discussed in detail in Chapters 6 and 8. The key point here is that the inhibitor binds the active site with greatest affinity in a conformational state other than the state binding substrate. In one example of this type of mechanism, the inhibitor initially binds to the active site in the substrate binding conformation (and therefore initial inhibitor binding would be competitive with substrate). Subsequent to initial inhibitor binding, however, a conformational change occurs, leading to a new state of the enzyme that binds the inhibitor much more tightly. Because this new state does not bind substrate, large concentrations of substrate are unable to overcome inhibition by the compound; the inhibition is said to be insurmountable by substrate (Figure 3.14B). Hence, an inhibitor that bound through a two-step kinetic process would appear noncompetitive (see Chapter 6 for more details).
Finally, for enzymes that act on proteins (or other macromolecular substrates), it is possible that most of the binding energy for enzyme–substrate complex formation is localized to recognition surfaces outside of the enzyme active site. In such a case, the binding of an inhibitor to the enzyme active site would abrogate catalysis, but would not be likely to disrupt enough of the binding energy to interfere with enzyme–substrate complex formation (Figure 3.14C). Hence, in this case, too, the inhibitor would appear noncompetitive in steady state analysis. This last situation is discussed further in Section 3.7.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree