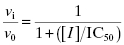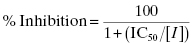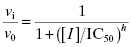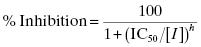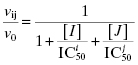5.1 Concentration–Response Plots and IC50 Determination
In Chapter 4 we briefly introduced the term IC50. Here we will describe its determination and meaning in greater detail. For any enzyme inhibitor that binds reversibly to a single site on an enzyme molecule (i.e., a 1-to-1 binding stoichiometry), one expects that binding, hence inhibition, will be saturable. At any concentration of inhibitor, the total concentration of enzyme in the sample is, by mass-balance, equal to the sum of the concentration of free enzyme molecules and the concentration of enzyme-inhibitor complex (see Appendix 2). The fractional activity (vi/v0, as defined in Chapter 4) relates directly to the ratio of free enzyme concentration over total enzyme concentration. The fraction of enzyme occupied by inhibitor will, again based on mass-balance, be 1 − (vi/v0), and the % inhibition is therefore 100(1 − (vi/v0) ). Thus, at a fixed concentration of enzyme and of substrate, the reaction velocity will diminish with increasing concentration of inhibitor until no residual activity remains (except in the case of partial inhibition, as discussed in Chapter 3, but here we are restricting our attention to dead-end inhibitors). If we were to plot the fractional velocity remaining as a function of inhibitor concentration, we would obtain a plot similar to that illustrated in Figure 5.2. Figure 5.2A illustrates a typical concentration–response plot (also referred to as a dose–response plot, although strictly speaking, the term dose should be reserved for in vivo administration of a compound) for a well-behaved enzyme inhibitor; Figure 5.2B illustrates the same data as a semilog plot. Note that on the semilog scale, the fractional velocity is a sigmoidal function of inhibitor concentration, displaying a plateau value of 1.0 at low concentrations of inhibitor and a second plateau of zero at high concentrations of inhibitor. The midpoint of this sigmoidal function occurs at a fractional velocity value of 0.5, corresponding to 50% inhibition of the target enzyme. The concentration of inhibitor that corresponds to this midpoint value is referred to as the IC50 as illustrated in Figure 5.2B.
Figure 5.2 Concentration–response plot for an enzyme inhibitor displayed on linear (A) and logarithmic (B) concentration scales. The IC50 is identified from the midpoint (i.e., fractional activity = 0.5) of the semilog plot.
Fractional velocity as a function of inhibitor concentration, as illustrated in Figure 5.2, can be fit to a simple binding isotherm equation (see Appendix 2):
The IC50 can thus be accurately determined by fitting the concentration–response data to Equation (5.1) through nonlinear curve-fitting methods. Some investigators prefer to plot data in terms of % inhibition rather than fractional activity. Using the mass-balance relationships discussed above, we can easily recast Equation (5.1) as follows:
Plotting the data as % inhibition as a function of inhibitor concentration again yields a sigmoidal curve, with the IC50 defined by the midpoint (50% inhibition) of the inhibitor titration. Now, however, the semilog plot will have the plateau at low inhibitor concentration corresponding to a % inhibition of zero, and the plateau at high inhibitor concentration corresponding to a % inhibition of 100. Thus the concentration–response plots now has the opposite directionality as those shown in Figure 5.2; the y-axis values go from a minimum (zero) at low inhibitor concentration to a maximum (100%) at high inhibitor concentration. One will find concentration–response data in the literature plotted using both fractional activity and % inhibition as the y-axis parameter; either method is acceptable and provides the same information.
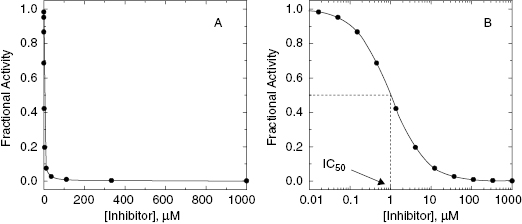
In practice, it is often convenient to perform the inhibitor titration (i.e., concentration-response experiment) in 96-, 384-, or 1536-well microwell plates. One convenient 96-well plate template for inhibitor titration is illustrated in Figure 5.3. Here one of 12 columns of the plate is used to measure the velocity of positive and negative control samples. The positive control wells contain the uninhibited enzyme (the average value being used to define v0). The negative control wells contain samples for which one can reasonable expect the enzymatic velocity to be zero (full reaction mixture in the absence of enzyme, or full reaction mixture with enzyme plus a saturating concentration of a known inhibitor, etc.); the average value of the negative control wells is used to establish the background velocity (i.e., background signal) of the assay. The other 11 columns are used to measure the velocity of the enzyme at varying concentrations of different inhibitors in replicate. The design displayed in Figure 5.3 relies on 11 inhibitor concentrations following a 3-fold serial dilution scheme, spanning a concentration range of 50,000-fold, with each inhibitor concentration tested in duplicate (see Appendix 3 for an explanation of serial dilution schemes). This allows one to construct a concentration–response plot, and thus determine IC50, for up to 4 inhibitors in a single 96-well plate.
Figure 5.3 A convenient scheme for performing an inhibitor titration in 96-well format. Four compounds (1–4) are assessed in duplicate at each of 11 inhibitor concentrations. The inhibitor concentrations follow a threefold serial dilution from a maximum concentration of 1000 (molarity units; nM, μM, etc.). The right-most column of wells is reserved for control samples. In this illustration four of the wells of column 12 are used for zero inhibitior positive controls, and the other four are used to establish the assay background as negative controls. Negative controls could represent any sample for which one knows that the enzymatic reaction has be abrogated. For example, the negative control wells could contain all of the reaction mixture components except the enzyme. See Chapter 4 for other potential forms of negative controls.
In an experimental design such as illustrated in Figure 5.3, it is common for the researcher to average the two duplicate determinations for each inhibitor concentration, and to construct the concentration–response plot using these averaged values. However, the nonlinear fitting from which the IC50 value is determined will have greater statistical power if one instead plots all of the data points (i.e., two points per inhibitor concentration in our example) on the same plot for curve fitting. The reason for this is that the degrees of freedom for the curve fitting is defined by n − 1, where n is the number of data points used for fitting. When one averages the duplicate values, the degrees of freedom for curve fitting is 11 − 1 = 10. If instead one plots all of the data individually for each inhibitor, the degrees of freedom will now be 22 − 1 = 21. Thus it is best to determine the IC50 value of an inhibitor by plotting all of the replicate data points on a single plot and use all of these data for curve fitting.
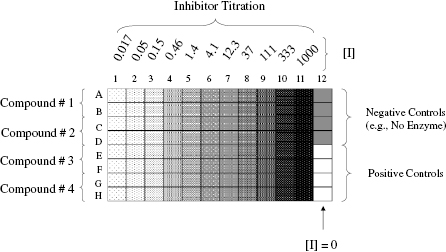
The IC50 value defines the concentration of inhibitor required to half-saturate the enzyme population under specific assay conditions and is commonly used as a measure of relative inhibitor potency among compounds. Thus IC50 values are typically used to rank-order the potency of validated hits from a high-throughput screen, but there are some important caveats to the use of IC50 values as a measure of relative potency. Changes in solution conditions, such as pH, ionic strength, and temperature, can significantly perturb the measured IC50 value. Thus these conditions must be maintained constant when comparing data for different inhibitors. For these same reasons caution must be exercised in comparing IC50 values from one laboratory to another (e.g., comparing ones own data with literature values). In the context of comparing the relative potency of different leads, the most important factor influencing the IC50 value is the substrate concentration used for inhibitors of differing modalities. Referring back to the velocity equations for competitive, noncompetitive, and uncompetitive inhibition (presented in Chapter 3), we have already seen that the % inhibition measured at a single inhibitor concentration is affected by substrate concentration in dramatically different ways for these different inhibition modalities (see Chapter 4). Likewise the measured value of IC50 will vary dramatically with substrate concentration in different ways for competitive, noncompetitive, and uncompetititve inhibitors (Table 5.1). Figure 5.4 illustrates the effect of [S]/KM ratio on the measured IC50 for these three reversible inhibition modes. These data were simulated for inhibitors with equal affinity (Kd = 50 nM) for the enzyme form to which each binds. Clearly, measuring the IC50 at a fixed substrate concentration is not an appropriate measure of the relative affinity for inhibitors of differing modalities; we will discuss this point further in a subsequent section of this chapter. Nevertheless, IC50 values are very commonly used to rank-order the potency of various leads in the early stages of lead optimization efforts. This is largely because of the experimental convenience of performing inhibitor titration at a single, fixed substrate concentration. If, for the sake of convenience and efficiency, initial potency comparisons are to be made on the basis of IC50 values, then these experiments should be performed at a fixed substrate concentration of [S] = KM (vide supra). While this is still not an ideal measure of true potency, these conditions will at least ensure some balance between the opposing effects of substrate concentration on competitive and uncompetitive inhibitors and, as mentioned in Chapters 2 and 4, they are also likely to reflect close-to-physiological conditions for many enzymes.
TABLE 5.1 Characteristic Effects of Substrate Concentration on the IC50 Value for Reversible Enzyme Inhibitors of Different Modalities
| Inhibition Modality | Effect on IC50 a |
|---|---|
| Competitive | Increases linearly with increasing [S]b |
| Noncompetitive (α > 1) | Increases curvilinearly with increasing [S] |
| Noncompetitive (α = 1) | No change with increasing [S] |
| Noncompetitive (α < 1) | Decreases curvilinearly with increasing [S] |
| Uncompetitive | Decreases curvilinearly with increasing [S] |
a Patterns based on the Cheng-Prusoff equations.
b The IC50 increases linearly as a function of [S] for competitive inhibitors. The pattern appears curvilinear in Figure 5.4 because the x-axis in this figure ([S]/KM) is presented on a logarithmic scale.
Figure 5.4 Effects of [S]/KM ratio on the apparent IC50 value for competitive (closed circles), noncompetitive (closed squares; α = 1) and uncompetitive (open circles) enzyme inhibitors. Note that the x-axis is plotted on a logarithmic scale for clarity.
Source: redrawn from Copeland (2003).
A question that often arises is how large a difference in IC50 between two compounds is considered significant. This can be addressed statistically using a standard Student t-test (Spence et al., 1976).
(5.3)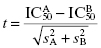 
where the indexes A and B identify the two inhibitors, and sA and sB are the standard errors or standard deviations associated with each IC50 value. If one uses the same number of data points to construct the concentration–response plot for both inhibitors, then the degrees of freedom for testing the significance of the t-value will be the combined total number of data points for the two inhibitors minus 2. Thus, if we are comparing two compounds for which each IC50 is determined from an 11-point titration in duplicate (vide supra), then the degrees of freedom would be (22 + 22) − 2 = 42. Knowing the degrees of freedom and the calculated t-value, one can determine if the difference in IC50 values between two inhibitors achieves statistical significance by reference to any standard table of t-values (see Spence et al., 1976, or any standard statistics text). If, for example, the standard error for each inhibitor is ≤10% of the IC50 value, a difference of 5-fold would be statistically significant with 95% confidence using this concentration–response scheme (Spence et al., 1976). The fold-difference in IC50 required to achieve statistical significance will, of course, increase with increasing error.
5.1.1 The Hill Coefficient
The concentration–response relationships presented in Equations (5.1) and (5.2) reflect ideal behavior for inhibition due to stoichiometric binding of one inhibitor molecule to one enzyme molecule. There are, however, situations in which this 1-to-1 binding does not properly describe the inhibition mechanism. In some cases the active enzyme species may consist of an oligomeric form, containing multiple, equivalent catalytic active sites (Copeland, 2000). The binding of a ligand (e.g., an inhibitor) to one of these multiple active sites may influence the affinity of the other active sites for the same ligand, in a process referred to as cooperativity. The binding of ligand at one active site can enhance the affinity of the other active sites for the ligand, and this is referred to as positive cooperativity. In other cases ligand binding at one site diminishes the affinity of the other sites for ligand, in a process referred to as negative cooperativity. These effects are discussed more fully in Copeland (2000) and in Perutz (1990). In addition to cooperative effects among active sites in an oligomeric enzyme, there can be situations where complete inhibition of an enzyme molecule requires more than one inhibitor binding event, so that the stoichiometry of interaction is greater than 1-to-1. Alternatively, situations can arise where the binding of one molecule of inhibitor to, for example, an enzyme dimer is sufficient to abrogate the activity of both active sites of the dimer. Hence the apparent stoichiometry, in terms of catalytic active sites, would be less than 1-to-1 in this case. To account for these possible mechanisms, the concentration–response equation must be modified as follows:
or
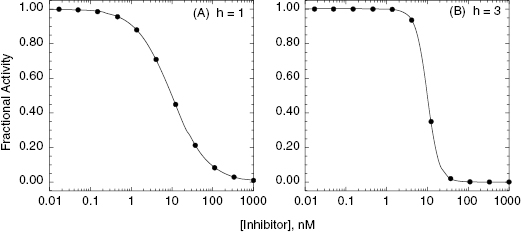
where the term h is referred to as the Hill coefficient or Hill slope (in honor of A. V. Hill, recipient of the 1922 Nobel prize in Physiology or Medicine), and is related to the stoichiometry of inhibitor–enzyme interactions. The Hill coefficient also represents the steepness of the concentration–response relationship. For a 1-to-1 binding event the concentration–response relationship dictates that to effect a change from 10% to 90% inhibition requires an increase in inhibitor concentration of almost two decades (an 81-fold change in inhibitor concentration to be exact). When the Hill coefficient is much greater than unity, this same change in % inhibition occurs over a much narrower range of inhibitor concentrations. As illustrated in Figure 5.5, very high values of the Hill coefficient change the concentration–response plot from a smooth, gradual change in effect (Figure 5.5A) to a situation where there is an abrupt switching between two extreme values of inhibition (Figure 5.5B).
Figure 5.5 Concentration–response plots for enzyme inhibition with Hill coefficients (h) of 1 (A) and 3 (B). Data simulated using Equation (5.4).
To account for differences in the Hill coefficient, enzyme inhibition data are best fit to Equation (5.4) or (5.5). In measuring the concentration–response function for small molecule inhibitors of most target enzymes, one will find that the majority of compounds display Hill coefficient close to unity. However, it is not uncommon to find examples of individual compounds for which the Hill coefficient is significantly greater than or less than unity. When this occurs, the cause of the deviation from expected behavior is often reflective of non-ideal behavior of the compound, rather than a true reflection of some fundamental mechanism of enzyme–inhibitor interactions. Some common causes for such behavior are presented below.
Aside from cooperativity and multiple, equivalent binding sites, a high Hill coefficient can be diagnostic of non-ideal inhibition behavior. Notably, compounds that cause an abrupt inhibition above a critical concentration, hence producing concentration-response relationships with h >> 1, usually reflect a nonspecific mechanism of inhibition. This can result, for example, for compounds that act as general protein denaturants or promiscuous inhibitors (see Chapter 4). Such compounds do not effect inhibition by a specific interaction with a defined binding pocket on the enzyme molecule and are therefore generally not tractable as drug leads. Likewise compounds that form micelles and inhibit enzyme function as the micelle will show a very abrupt concentration–response plot, reflecting not the response of the enzyme to inhibition per se but rather the critical micellar concentration (CMC) of the compound. Detergents, chaotrophic agents, aprotic and nonpolar solvents (e.g., DMSO, acetonitrile), and other nonspecific enzyme denaturants will also display high Hill coefficients when titrated in enzyme assays. None of these inhibition mechanisms are tractable from a pharmacological perspective. Hence the determination of a high Hill slope in the concentration–response plot for a compound should cause some skepticism regarding the value of that compound as a lead, and should thus trigger additional investigations. High Hill coefficients can also result from very tight binding of inhibitors to enzyme targets and from irreversible inhibition of enzymes. These special forms of enzyme inhibition are considered in detail in Chapters 6 through 9.
Concentration–response relationships displaying Hill coefficients much less than unity generally result from two origins. The first is a situation in which the inhibitor binds to more than one, nonequivalent binding pocket to effect full inhibition of activity. In some cases, this could reflect two nonequivalent binding pockets on the same enzyme molecule. For example, a number of antibiotics that act by binding to ribosomes have been demonstrated to display two inhibitor binding sites, a low-affinity binding site and a high-affinity binding site. In other cases, the multiple, nonequivalent binding pockets reside on separate enzyme molecules. This could be because the enzyme source being used contains more than one enzyme that contributes to the activity being measured in the assay, for example, if one were using a natural source, such as a cell lysate, without sufficient purification of the target enzyme. Alternatively, the nonequivalent binding pockets could reflect an equilibrium between two or more forms of a single enzyme. Suppose, for example, that an enzyme sample contained an equilibrium mixture of monomer and dimer forms of the target enzyme, both contributing to the overall activity being measured. If the inhibitor displayed differential affinity for the monomer and the dimer, this would result in multiple, nonequivalent binding. In any of these cases the resulting concentration–response plot would reflect the multiplicity of binding pockets for the inhibitor. Figure 5.6 illustrates the concentration–response plot for a situation in which there is one low-affinity (IC50 = 70 nM) and one high-affinity (IC50 = 0.3 nM) binding interaction for the inhibitor. In Figure 5.6A the data are fitted using Equation (5.4), as might happen if we were unaware of the multiplicity of binding interactions. The best fit to Equation (5.4) from these data yields an IC50 of 4.6 ± 0.8 nM and a Hill coefficient of 0.46 ± 0.03. A result like this should cause the investigator to question the validity of fitting the data to Equation (5.4). A careful visual inspection of the data might cause the investigator to suspect the presence of more than one binding interaction and therefore to fit the data to a more appropriate equation (see Copeland, 2000 and caption to Figure 5.6) as illustrated in Figure 5.6B. In a situation like this, the investigator would need to explore the origin of the multiple binding events to determine if this is a true characteristic of the target enzyme or an experimental artifact.
Figure 5.6 Biphasic concentration-response plot for an enzyme displaying a high- and low-affinity binding interaction with an inhibitor. In panel A, the data are fit to Equation (5.4) and the best fit suggests a Hill coefficient of about 0.46. In panel B, the data are fitted to an equation that accounts for two, nonidentical binding interactions: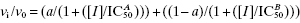 
, where a is an amplitude term for the population with high binding affinity, reflected by 
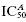, and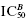 
is the IC50 for the lower affinity interaction. (See Copeland, 2000, for further details.)
The second common cause of a low Hill coefficient is a partitioning of the inhibitor into an inactive, less potent, or inaccessible form at higher concentrations. This can result from compound aggregation or insolubility. As the concentration of compound increases, the equilibrium between the accessible and inaccessible forms may increase, leading to a less than expected % inhibition at the higher concentrations. This will tend to skew the concentration–response data, resulting in a poorer fit to Equation (5.4), with the best fit obtained when h << 1.0. As an example, suppose that we were studying a natural protein or peptide inhibitor of a target enzyme that inhibited the enzyme well as a monomer but with significantly less affinity as a dimer. If the dissociation constant for the dimer-monomer equilibrium is similar in magnitude to the IC50 of the monomer for inhibiting the enzyme, then both the monomer and dimer species will be significantly populated over the course of the concentration–response study. If the dissociation constant for dimer-monomer equilibrium is given the symbol Kdimer, it can be shown that the fraction of monomer in solution (δ) at any total concentration of inhibitor (C), is given by the following equation (Weber, 1992):
(5.6) 
The concentration of monomer present at any concentration of inhibitor is given by δC, and the concentration of dimer is given, considering mass balance, by (1 − δ)C. When an enzyme is treated simultaneously with two inhibitors, I and J, that bind in a mutually exclusive fashion, the fractional activity is given by (Chapter 3 and Copeland, 2000)
If I represents the monomer and J represents the dimer of our inhibitory molecule, then Equation (5.7) becomes
(5.8)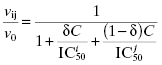 
In this case, fitting the concentration–response data to Equation (5.4) would yield a smooth curve that appears to fit well but with a Hill coefficient much less than unity.
In all these situations the Hill coefficient provides a warning sign to the medicinal chemist that the physical properties of the compound may render it intractable for further consideration. In short, whenever the Hill coefficient is significantly different from unity, the experimental data and the quality of the lead compound must be scrutinized much more carefully.
5.1.2 Graphing and Reporting Concentration–Response Data
Graphing and fitting of the inhibtor concentration–response data to obtain the IC50 is typically the primary mechanism for assessing the relative potency of lead compounds and lead compound analogues (see below). The IC50 can be determined by visual inspection of the concentration–response plot, but today it is more appropriate and more common to determine the IC50 by nonlinear curve fitting of the data. In some laboratories, especially where a high volume of compounds are being evaluated, this process has been completely automated, so that the IC50 determination is done directly from the raw data of the assay by the computer-based instrumentation system in the laboratory. This is a very efficient mechanism for generating IC50 values for large numbers of compounds. However, there is still great value in visual inspection of concentration–response plots, especially to diagnose non-ideal behavior.
In processing raw data from assays to produce concentration–response plots for IC50 determinations, many investigators allow the minimum value of fractional activity or % inhibition, and the maximum value of these parameters, to float as fitting parameters. Hence the nonlinear curve fitting represents a four-parameter fit, the four parameters being y-axis minimum, y-axis maximum, IC50, and Hill coefficient. I disfavor this type of curve fitting because it often makes recognition of problematic data difficult from visual inspection of the concentration–response plots. Also it can lead to data fitting that is not consistent with the physical reality of the experiment. To illustrate this point, consider the concentration–response plots presented in Figure 5.7. In Figure 5.7A the data are fit to a four-parameter equation, and the y-scale goes from 20% inhibition to 100% inhibition. The fitted line goes smoothly through the data, and it is easy to conclude, from a quick glance, that this was a well-behaved inhibition plot. More careful inspection, however, reveals that the minimum plateau value at low [I] corresponds to 20% inhibition. Since this is a plateau value, it means that at infinitely low, or zero concentration of inhibitor, the enzyme is inhibited by 20%. Since the value of v0, from which fractional activity and % inhibition are calculated, is based on measurement at zero inhibitor concentration, the idea of 20% inhibition in the absence of inhibitor makes no physical sense. Something is not right about these data, and this point is much more evident to the investigator when the data are fit to the two-parameter equations presented earlier in this chapter (Equations 5.1–5.5) and plotted on a graph for which the y-axis goes from 0 to 1 (for fractional activity) or 0 to 100 (for % inhibition; see Figure 5.7B). A nonzero plateau at low inhibitor concentration might reflect a second, higher affinity binding interaction. A result like this would require additional experimentation, with the concentration range of inhibitor extended to much lower values.
Figure 5.7 Comparison of four-parameter (y-maximum, y-minimum, IC50, and h) and two-parameter (IC50 and h) fits of non-ideal concentration–response data. In panels A and B the data indicate a nonzero plateau at low inhibitor concentration that might reflect a low-amplitude, high-affinity second binding interaction. In panels C and D the data indicate a plateau at high inhibitor concentration that does not achieve full inhibition of the enzyme. There could be multiple causes of behavior such as that seen in panels C and D. One common cause is low compound solubility at the higher concentrations used to construct the concentration–response plot. Note that the discordance between the experimental data and the expected behavior is most immediately apparent in the plots that are fitted by the two-parameter equation.
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
