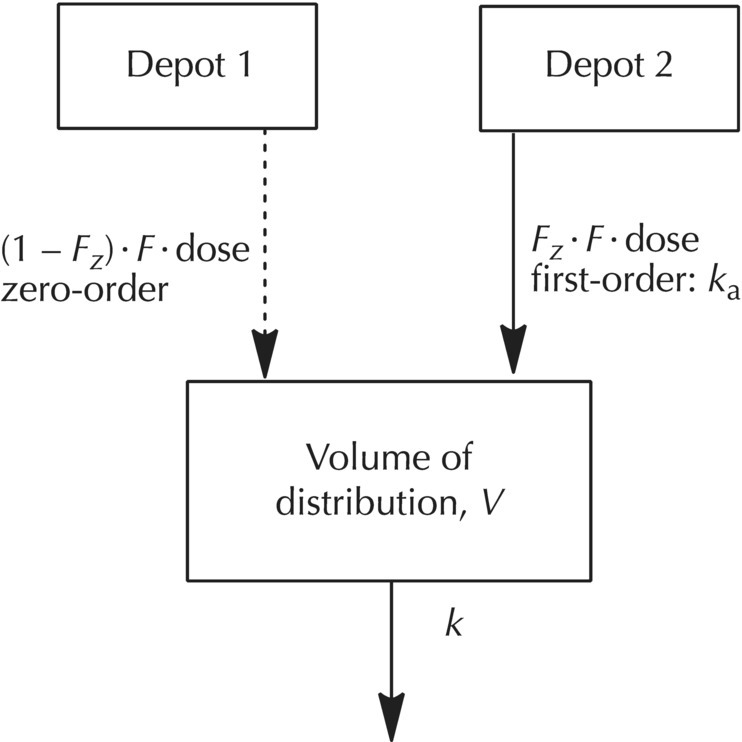
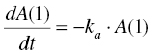Chapter 9 Nonlinear mixed effect models are useful for the construction of an immense variety of pharmacometric models. The PRED and PREDPP routines of NONMEM provide flexibility to describe complex models and are not limited to the set of prebuilt models provided in the specific ADVAN routines (ADVAN1, 2, 3, 4, 10, 11, and 12) or to a limited set of numbers of compartments or functional forms for rate and transfer processes. Our use of the expression user-written model does not simply mean writing a control file. The use of any model in NONMEM requires a user-written control file that includes elements such as code to call the dataset, the names of the parameters to be estimated, specification of the fixed- and random-effect parameter structures, and initialization of parameter values. The expression user-written models in this chapter refers to control files in which the complete mathematical structure of the model must be specified by the analyst. We will focus on the expression of these user-written models using PREDPP, including models not specified with the specific ADVANs, which must be defined specifically by the analyst using the general ADVANs (5, 6, 7, 8, 9, and 13). For pharmacokinetic (PK) analysis, perhaps the most common need for user-written models is to describe the complex nature of drug absorption rather than an unusual arrangement or number of compartments in a model. Recirculation, transit compartments, and nonlinear elimination or transfer processes are other settings in which the need for more complex PK models is frequently encountered. For the analysis of pharmacodynamic data, user-written models are generally required except in the simplest cases. Chatelut et al. (1999) provide an interesting example of a PK scenario that we will use to demonstrate various ways to code user-written models. The authors describe a variety of models that were tested in the PK model development process for alpha interferon, one of which described the PK properties with a one-compartment model disposition with simultaneous first-order and zero-order absorption without a lag time. One way to describe this model is to describe an absorption, or depot, compartment for each rate process and estimate the fraction absorbed through each process. Figure 9.1 depicts the schematic diagram of a model that can be used to describe these simultaneous processes, where the variable Fz is the fraction of the dose absorbed by the first-order rate, 1 – Fz is the fraction of the dose absorbed by the zero-order rate, V is the volume of distribution in the body, and k is the first-order elimination rate constant. With this basic compartmental model structure, a variety of absorption processes can be described, including: Some arrangements of the model features listed can be dealt with using the specific ADVANs (e.g., ADVAN1 or ADVAN2), while other arrangements require user-defined model structures in the general linear or nonlinear ADVANs. Some of these aspects will be briefly described here, with more detailed description and code examples to follow later in this chapter. Figure 9.1 Simultaneous absorption model. (Adapted from Chatelut et al. (1999). Copyright © 2001, John Wiley & Sons. All rights reserved.) If two sequential first-order absorption processes are to be modeled, a single absorption compartment in a specific ADVAN might be used to describe both processes, using the model-change-time parameter (MTIME) in NONMEM. However, the specific ADVANs include at most one absorption site with a single first-order input rate constant. When two or more parallel first-order absorption sites with different rates of input are to be modeled, a separate absorption compartment is needed to account for the mass transfer from each site. Each depot compartment will have a first-order absorption rate constant (e.g., KAFAST and KASLOW). This scenario can be described using a general ADVAN and a model with two depot compartments. The fraction of the dose entering each of two (or more) depot compartments must be constrained using an approach like that shown in Figure 9.1 using the parameter Fz. Without such constraints, it would be possible for the system to have errors such as adding more drug to the depot compartments than the actual dose amount. This error can occur because using this approach requires that two dosing records be included in the dataset, one for each absorption compartment. The full dose amount must be included in the AMT variable for each depot compartment. As illustrated in Figure 9.2, the Fz and 1 – Fz parameters partition the absorbed dose between the two depot compartments. Figure 9.2 Illustration of the partitioning of the administered dose. Individually, Fz and 1 – Fz do not represent the absolute bioavailability fraction, F, that we usually consider. F is the total fraction of the administered dose that will be absorbed by any route. Fz represents that fraction of F that will be absorbed through the first-order absorption process. Intravenous data and an alternate coding method would be required to accomplish the simultaneous estimation of the true absolute bioavailability fraction and the fractions of the absorbed dose that are absorbed by each oral absorption process, whether those are both by first order, or by first- and zero-order processes. In this model, the volume of distribution, V, is the proportionality between observed concentrations in the plasma and the concurrent amount of drug in the body (excluding the absorption sites). The first-order elimination rate constant is denoted k. This modeling approach will be explained in greater detail later in this chapter. At this point, the example is included to demonstrate an occasion in which a user-written model is needed to express a particular PK model. The standard ADVAN2 routine can be used to model data following the administration of both oral and intravenous doses, another example of a combination of first- and zero-order processes similar to the Chatelut et al. (1999) example explained earlier. Use of ADVAN2 is possible in this case because the specific dose amount administered by the oral and intravenous routes would be known. In the alpha interferon example given earlier, a single dose is administered subcutaneously, yet the dose is absorbed by two different absorption rate processes. Since the fraction absorbed by each rate process is not known and must be estimated, this problem is somewhat more complex. Similar scenarios arise when a dose is administered by nasal or oral inhalation, and part of the dose is absorbed locally, while part is swallowed and absorbed at a different rate in the gastrointestinal (GI) tract. Estimating the fraction absorbed at the two sites is important for an accurate description of the absorption process. When using PREDPP, the implementation of user-written models is achieved using one of the PREDPP subroutines ADVAN5, 6, 7, 8, 9, or 13. Use of each of these ADVANs requires a $MODEL block to define the number and properties of the compartments of the model. Compartments are named and properties given using a COMP statement for each compartment in the model. For example, a two-compartment model with parallel zero-order and first-order absorption compartments could be specified as shown in Figure 9.3. Figure 9.3 Two-compartment model with parallel zero-order and first-order drug absorption. Specification of the $MODEL statement for this scenario might be coded as follows: Here, DEPOT1, DEPOT2, CENTRAL, and PERIPHERAL are arbitrary names, while DEFDOS and DEFOBS are NONMEM-defined terms with specific meaning. Any alphanumeric name that is not a reserved name can be used to name the compartments, though the use of meaningful names will avoid confusion for the analyst. DEFDOS and DEFOBS define the default compartments for the dose and observation events, respectively. Defining these default properties is needed when the compartment (CMT) data item is not included in the dataset and NM-TRAN must assign the compartment for these events. DEFDOS and DEFOBS can be overridden by the use of CMT in the dataset. By specifying the appropriate compartment number on each dataset record, doses may be entered into and observations made from any compartment. The EVID item is used as it is with any specific ADVAN routine, to describe the type of record. Other compartment options exist, such as defining a compartment that can be turned off or on by default, but these are not used as frequently. Through PREDPP, NONMEM accounts for the mass in each compartment over time. Here, mass is used in a mathematical sense and may represent any dependent variable (DV), such as drug concentration, amount, or pharmacodynamic effect. For PK models, the units of predicted values (i.e., mass or concentration) are defined by the relationship of the dose units and the scale parameter of the observation compartment. The analyst must always take care to confirm that the scale parameter appropriately balances the units of predictions and the units of the observations in the dataset, for each compartment in which observations are made. Use of the scale parameter was discussed in detail in Section 3.5.2.2. After the definition of the compartment structure of the model, the relationships between those compartments must be defined, as well as the general numerical analysis methodology that will be used to evaluate the model. The general methodology employed to specify and evaluate the model is governed by the ADVAN routine selected. The relationships and transfer between compartments are generally defined by the parameters and equations in the $PK, $DES, $AES, and $ERROR blocks, if present. The $PK and $ERROR blocks also have been described in Chapter 3 to some extent, but we will elaborate here on the use of these and other blocks for the construction of user-written models. Selection of a particular ADVAN is accomplished using the $SUBROUTINES statement. When differential equations are used (ADVAN 6, 8, 9, and 13), the number of significant digits to be carried to be accurate in the computation of the compartment amounts must also be specified. This value can be defined using the variable TOL on the $SUBROUTINES statement, for example, $SUBROUTINES ADVAN6 TOL = 4. One may consider changing the value of TOL when numerical difficulties are encountered during estimation, when run times are excessively long, or when greater precision in the results is required. The optimal TOL value for a particular problem is a balance between the informativeness of the data, the complexity or nonlinearity of the model, and the precision of the final parameter estimates required. Alternatively, a $TOL statement may be used to define this value. If needed, with ADVAN9 and 13, separate values can be assigned to the different compartments of the model. TOL is not the number of significant digits in the final parameter values but is related to the number of significant digits used internally for computation of the mass in the compartments. ADVAN5 and ADVAN7 allow the expression of multicompartment models composed of exclusively first-order transfer between compartments. These ADVANs require the control file to state the number of compartments and to define the transfer links between compartments. Models using ADVAN5 and ADVAN7 generally execute more quickly than those that require the expression of the model as differential equations. While model compartments are defined using the $MODEL statement, links between compartments are defined in the $PK block using first-order rate constants with the letter K followed by numerical index values defining compartment numbers of the source and destination of mass transfer. For example, the parameter K12 defines first-order transfer from compartment 1 to compartment 2. The first index value is the source compartment, and the second index value is the destination compartment. When greater than nine compartments are present, causing the compartment numbers to increase to two-digit numbers, the index values are separated by the capital letter T. For example, transfer from compartment 1 to compartment 10 would be coded as K1T10. Elimination of drug from the body is coded with an index value of 0 for the output compartment. Thus, K20 represents the first-order transfer of drug from compartment 2 out of the body (e.g., into the urine). Consider a three-compartment model with first-order absorption with a catenary arrangement of compartments as shown in Figure 9.4. Figure 9.4 Catenary compartment model with first-order absorption. ADVAN5 and ADVAN7 require that the microrate parameters of transfer be defined as described earlier. However, these may be transformed into any other set of parameters desired. The code below could be used to describe the model in Figure 9.4 in parameters of clearance and volume terms using ADVAN5:
User-Written Models
9.1 Introduction
9.2 $MODEL
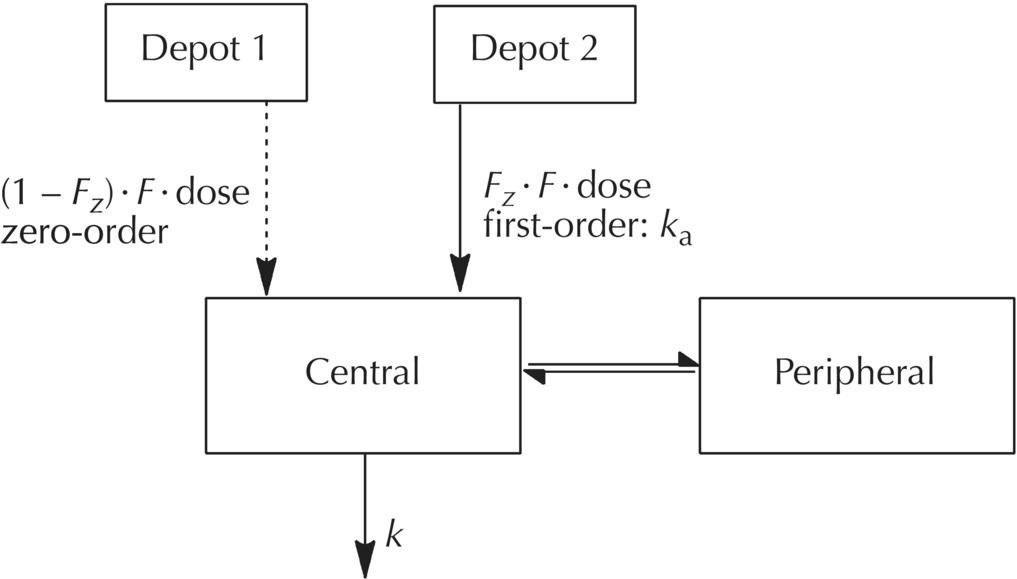
$MODEL
COMP(DEPOT1, DEFDOS)
COMP(DEPOT2)
COMP(CENTRAL, DEFOBS)
COMP(PERIPHERAL)
9.3 $SUBROUTINES
9.3.1 General Linear Models (ADVAN5 and ADVAN7)
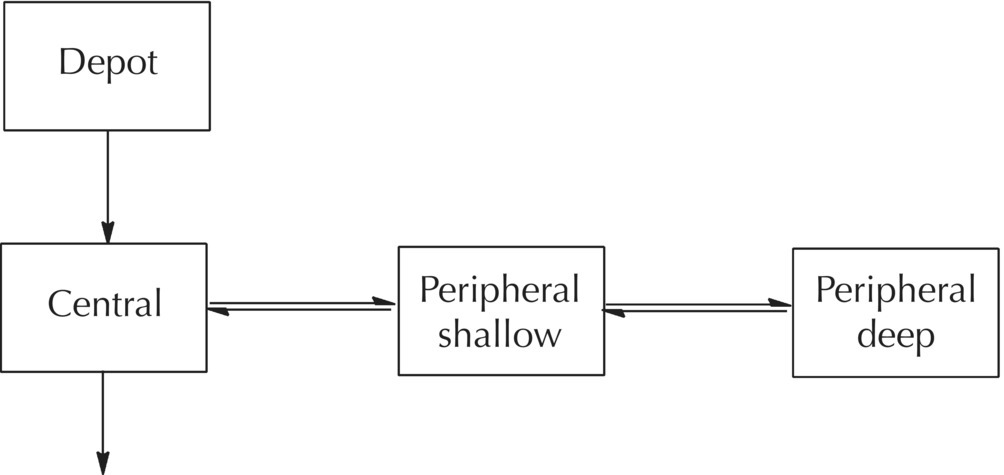
$PROBLEM Catenary 3-compartment model with first-order absorption
$INPUT ID TIME AMT DV CMT EVID MDV
$DATA filename
$SUBROUTINES ADVAN5
$MODEL ; define the parameters of the
COMP (DEPOT, DEFDOS) ; model
COMP (CENTRAL, DEFOBS)
COMP (PSHALLOW)
COMP (PDEEP)
$PK
KA = THETA(1)*EXP(ETA(1)) ; Modeled using Cl & V terms
V2 = THETA(2)
CL = THETA(3)*EXP(ETA(2))
Q1 = THETA(4) Q2 = THETA(5)
V3 = THETA(6)
V4 = THETA(7)
K12 = KA ; Micro-rate parameter
K20 = CL/V2 ; definitions are required
K23 = Q1/V2 ; for ADVAN 5 & 7
K32 = Q1/V3
K34 = Q2/V3
K43 = Q2/V4
Through the simple constructs of ADVAN5 and ADVAN7, using only the $MODEL statement and the definition of first-order rate constants in the $PK block, a wide variety of mammillary, catenary, or other models may be easily defined. However, the analyst must always consider whether the model defined is reasonable for its purpose, whether it is identifiable, and whether the data collected are sufficient for the estimation of the model parameters.
9.3.2 General Nonlinear Models (ADVAN6, ADVAN8, ADVAN9, and ADVAN13)
The general nonlinear ADVANs use differential equations to describe the properties of the model and allow nonlinear relationships for mass transfer. A differential equation describing the rate of change of mass in the compartment must be included for each compartment of the model. In addition to the use of differential equations, ADVAN9 also allows the expression of the compartment mass using algebraic equations. Some of the NONMEM literature refers to these as equilibrium compartments. The use of differential equations to express the model gives almost limitless freedom to define the system and is at the heart of the great flexibility of NONMEM.
The major difference between these ADVANs is the particular differential equation solvers used by each for the estimation of model parameters. Some of the methods are optimized for stiff versus nonstiff differential equations (ADVAN8 versus ADVAN6) or use various other numerical methods to solve the differential equations (ADVAN9 and ADVAN13). A discussion of these differences is beyond the scope of this text. However, one approach to selecting the preferred ADVAN method for a particular model and dataset was suggested to the authors in personal communication with Dr. Beal. The method entails writing a control file for each method one wants to compare. The next step is to set MAXEVAL = 1 on the $ESTIMATION record line and run the models. Based on comparison of the output from each method, the method that gives a successful first iteration most quickly is likely the method to be preferred for the particular model and dataset combination.
9.3.3 $DES
In pharmacometric applications, systems of differential equations are used to express the instantaneous rate of change of mass (i.e., mass, concentration, or effect) in each compartment of a model. The $DES block contains the system of equations, with one equation for each compartment. Each equation is stated using an indexed expression, DADT(i), where i is the compartment number. For example, the first-order disappearance of drug from the depot compartment might be expressed as DADT(1) = –KA*A(1). Here, A(1) is the mass in compartment 1 at the current instant in time.
Equations can be expressed where the rate of change of drug in the compartment is dependent upon the amount of drug in more than one compartment. For instance, the rate of change in concentration in the central compartment of a two-compartment model with first-order absorption and elimination might be expressed as DADT(2) = KA*A(1) – (K23 + K20)*A(2) + K32*A(3). A differential equation must also be written to describe the transfer of drug in and out of the peripheral compartment. Thus, a two-compartment disposition model with first-order absorption will actually be expressed as a model with three compartments that are typically numbered as (1) depot, (2) central, and (3) peripheral. The complete system for the model could be stated in the $DES block as:
$DES
DADT(1) = –KA * A(1)
DADT(2) = KA * A(1) – (K23 + K20) * A(2) + K32 * A(3)
DADT(3) = K23 * A(2) – K32 * A(3)Inclusion of the absorption, or depot, compartment leads to a renumbering in the NONMEM code of index values from the typical numbering that might be used in the literature to describe a model. For instance, we typically define the transfer of drug from the central to the peripheral compartment of a two-compartment model as K12, regardless of the route of administration. Thus, in our aforementioned example, the value K23 corresponds to the traditional parameter K12. Care must be used in the presentation of final parameter values so their meaning is clear to the reader. Parameterization of models in terms of clearance and volume does not remove this problem since these terms are also indexed based on the index values of the NONMEM compartments, which may vary depending upon the route of drug administration. This issue is not necessarily specific to NONMEM, but is common to any full expression of the PK system to include compartments for absorption.
In this example of a two-compartment model, KA, K23, K20, and K32 are fixed-effect parameters that must be defined in the $PK or $DES blocks and assigned initial values in the $THETA block. NM-TRAN does not have expectations for the parameters of models written with any of the general ADVANs, and the analyst must be careful to correctly define each parameter needed in the model. It is not always necessary, or possible, to estimate every parameter in a model. Some parameters may be fixed to a certain value and not estimated (Wade et al. 1993). The implications of this parameter value assignment to the questions being addressed should be specifically assessed by the analyst where appropriate.
The two-compartment model with first-order absorption is specifically implemented in ADVAN4. When appropriate, the use of ADVAN4 is preferable over the statement of the same model using $DES in a general ADVAN since it may be coded more easily and will execute much more quickly. However, the ability to express the model using the $DES block allows one to easily modify the model and express other models with modifications to this basic structure. For instance, a more complex model might be required to describe the absorption process of a particular drug. Use of ADVAN4 allows for either first-order or zero-order drug input. In both cases, the amount of each dose must be specified using the AMT variable. First-order input is invoked by defining the parameter ka. Zero-order input can be achieved using the RATE and AMT data items in the dataset and by defining the duration parameter in $PK, as discussed previously in Chapter 4. Beyond simple first- and zero-order input, some absorption models will require the use of multiple absorption compartments with a variety of expressions of the transfers between these compartments.
When modeling in a $DES block, the current value of time is available in the variable T. This value is more continuous in nature than the discrete steps of time (i.e., TIME) in the records of the dataset. The step size for T is a function of the numerical algorithm in use. Sometimes in the $DES block, the use of T, rather than TIME, can improve the stability of a nonlinear model, particularly one with time-dependent parameters.
9.4 A Series of Examples
Several examples will be used to illustrate a variety of approaches for the coding of user-written models. The first examples do not require a general ADVAN to state the problem, although there is unique coding required for each case. The later example demonstrates the use of the general nonlinear ADVANs. The general examples of user-written models presented in this chapter include complex absorption patterns and a nonlinear metabolite model.
9.4.1 Defined Fractions Absorbed by Zero- and First-Order Processes
Consider a hypothetical example where a 300-mg dose of a drug is orally administered in a controlled-release formulation. For the sake of simplicity, we will assume that the first 100 mg undergoes immediate release with no lag time for absorption, the remaining 200 mg is released via a controlled-release formulation, and bioavailability of the compound is complete (i.e., 100%). The formulation is designed such that the second portion of the dose is released beginning at two hours after administration with a controlled-release mechanism that imparts a slower, zero-order absorption process for the remainder of the dose. The first portion of the dose is considered as a bolus administered into the first-order depot compartment (CMT = 1), while the second portion of the dose can be thought of as an infusion directly into the central compartment. A conceptual diagram of this scenario is shown in Figure 9.5. The zero-order depot is conceptual and need not be explicitly included in the model. The zero-order dose can simply be coded as a zero-order infusion directly into the central compartment (CMT = 2).
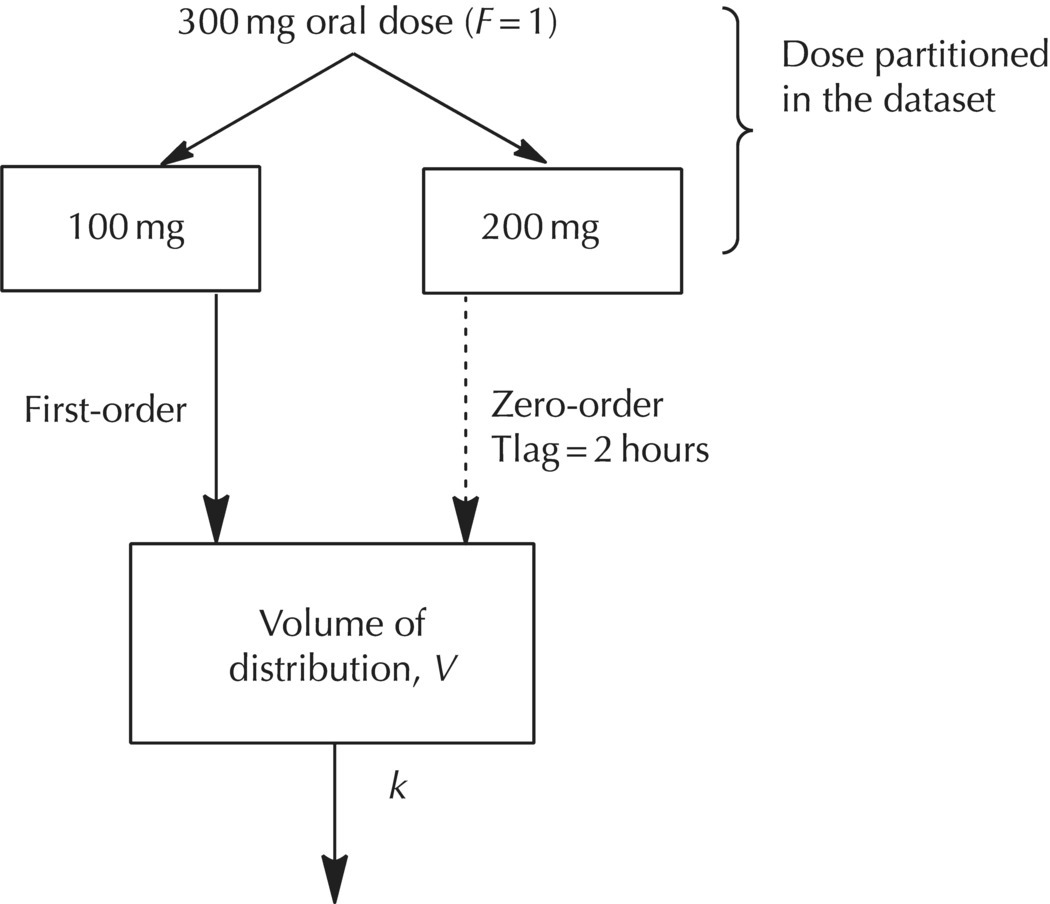
Figure 9.5 One-compartment model with first-order and zero-order absorption, dose fractions known and complete bioavailability.
Note that the fractional split of the dose between compartments and the time of release for the second compartment are assumed to be known. With these simplifications, the expression of this model can be achieved using ADVAN2. To code the model, the total dose of the drug is divided between two compartments, one with a fast first-order absorption rate and one with a slow zero-order absorption rate. In this simple example, the fraction of the dose absorbed according to each rate is assumed based on the design of the dosage form. When the fraction for each component is known, splitting the dose into two compartments is a simple step implemented during dataset construction. Two dosing records are needed for each individual dose administered, and the doses would be assigned to CMT = 1 (AMT = 100) for the fast portion and CMT = 2 (AMT = 200) for the slow portion. The first single dose for the first subject might be coded in the first two dosing records as shown in Table 9.1.
Table 9.1 Example dosing records for simultaneous bolus and zero-order input: fixed amounts through each route
| ID | TIME | DV | AMT | EVID | RATE | MDV | CMT |
| 1 | 0 | . | 100 | 1 | 0 | 1 | 1 |
| 1 | 0 | . | 200 | 1 | –2 | 1 | 2 |
A portion of the control file must consist of defining the model parameters. The delay in the beginning of the slow drug absorption process could easily be included using an indexed lag-time parameter, ALAG(i), which is available within PREDPP for every compartment. If we assume we know the time the second absorption process begins, we can fix the value of ALAG in the control file (e.g., ALAG2 = 2, since absorption is expected to begin two hours after the dose). Alternatively, if the lag is anticipated to differ between doses based on treatment differences, we can include the lag time (e.g., LAGT) as a data item, then set ALAG2 = LAGT in the control file. LAGT in the dataset would contain the value specific to the treatment.
For this example, the initial portion of the control file might be constructed as follows:
$PROBLEM First- and Zero-Order Abs.; Known Fractions; F=1
$INPUT ID TIME DV AMT EVID RATE MDV CMT
$DATA filename
$SUBROUTINES ADVAN2 TRANS2
$PK
KA = THETA(1)*EXP(ETA(1))
ALAG2 = 2 ; Lag for start of zero-order
D2 = THETA(2) ; Duration of zero-order input
CL = THETA(3)*EXP(ETA(2))
V = THETA(4) ; Central compartment volume
K = CL/V ; Elimination rate constantUse of the RATE data item and D2 parameter allows the duration of the zero-order input process to be estimated. The process begins at time ALAG2 = 2 and continues until the entire drug amount from this process has been absorbed. The duration of that process is estimated through the D2 parameter, based on the best fit of the data. The rate of absorption can be calculated as Rate = AMT/D2. The units of the zero-order rate of input are mass per unit time.
In more common situations, when we do not assume we know the time the second absorption process begins, we can use ALAG2 = THETA(i). Here, the estimate of THETA(i) gives the value of the lag time, and no drug absorption from the second compartment begins until time is greater than ALAG2. In this simple example, drug absorption continues from the fast first-order compartment until the entire amount of drug that will be absorbed from that compartment has been absorbed. Absorption from the slow zero-order compartment begins at TIME = ALAG2 and continues until the entire drug amount that will be absorbed from this route has been absorbed. The two processes may continue simultaneously after TIME reaches ALAG2.
9.4.2 Sequential Absorption with First-Order Rates, without Defined Fractions
Another example includes a change in rate of absorption, but without specifically modeling the fraction absorbed at each rate. This change might occur because the solubility or permeability of the drug changes substantially as the drug proceeds down the GI tract. Consider a case where the absorption rate decreases with time because there is relatively faster absorption in the upper GI tract than the lower. This situation can be expressed using ADVAN2. The time of the change in rate can be defined using model-event-times (MTIME(i)) in PREDPP. Multiple model-event-times can be used, and these times are indexed sequentially. If there is only one event time, then MTIME(1) is the estimated time that (in this example) the absorption rate decreases. The event time is estimated by setting it equal to a fixed-effect parameter to be estimated, for example, MTIME(1) = THETA(1). The change in KA is implemented using a block of code to estimate each KA (e.g., KAFAST and KASLOW), using the logical indicator variable MPAST(1) to test whether the current time has passed the event time. Here, KA is a NONMEM-reserved name in ADVAN2. KAFAST and KASLOW are user-defined variable names. MPAST(i), a NONMEM-reserved word, is an indexed NONMEM-defined logical variable having the following values: MPAST(1) = 0 if TIME ≤ MTIME(1), and MPAST(1) = 1 if TIME > MTIME(1). The current value of KA is set based on the value of MPAST(1). For example:
KAFAST = THETA(1)
KASLOW = THETA(2)
MTIME(1) = THETA(3)
KA = KAFAST*(1-MPAST(1)) + KASLOW*(MPAST(1)) At times less than or equal to MTIME(1), MPAST(1) has the value 0, so KA = KAFAST. At times greater than MTIME(1), MPAST(1) has the value 1, so KA = KASLOW. Using this approach, this model too can be coded using ADVAN2. Also, only a single dosing record for each dose administered is needed, unlike the case above where a separate dosing record was needed for each depot compartment. Here, since we are using ADVAN2, there is only one depot compartment, and the change in absorption rate is mediated through a change in the absorption rate parameter.
9.4.3 Parallel Zero-Order and First-Order Absorption, without Defined Fractions
A more interesting challenge arises when the amount of the dose absorbed at each rate and the time at which absorption begins are not known. This is similar to the Chatelut et al. (1999) model described in Section 9.1. We can address this problem using a model with each dose administered in full into two compartments, and in which the fraction of the dose entering through each compartment is estimated. To implement such a model, two dosing records must be included in the dataset for each actual dose administered. One dose record is assigned to each of the two dosing compartments. However, the AMT variable on both dosing records should equal the entire dose amount. This scenario can be modeled using ADVAN2 where the depot compartment, CMT = 1, is associated with first-order input, and the zero-order input process directly enters the central compartment, CMT = 2, like an intravenous infusion. Dosing records might be structured as demonstrated in Table 9.2 for the first subject.
Table 9.2 Example dosing records for simultaneous bolus and zero-order input: estimated amounts through each route
| ID | TIME | DV | AMT | EVID | RATE | MDV | CMT |
| 1 | 0 | . | 300 | 1 | 0 | 1 | 1 |
| 1 | 0 | . | 300 | 1 | –2 | 1 | 2 |
The fraction of the absorbed dose that enters through the depot compartment is estimated by defining the NONMEM bioavailability parameter for that compartment as a parameter to be estimated, F1 (e.g., F1 = THETA(1)). The fraction of the absorbed dose entering through the second dosing compartment (i.e., the central compartment) is calculated by subtraction, F2 = 1 – F1, and thus partitions the administered dose between the two dosing compartments. If the bioavailability fraction were not used to partition the dose, the two dosing records could imply the absorption of twice the administered dose. These fractions, F1 and F2, are not the true bioavailability fractions, but are instead the fraction of the absorbed dose that is absorbed by each route. This distinction is illustrated in Figure 9.2. The following code demonstrates how this model can be implemented using ADVAN2 and is one way to code the scenario introduced in Figure 9.1:
$PROBLEM Parallel first-order and zero-order absorption
; with the fraction absorbed by each route to be
; estimated
$INPUT ID TIME AMT DOSE DV EVID RATE MDV CMT
$DATA study01.csv$SUBROUTINE ADVAN2
$PK
F1 = THETA(1) ; DEPOT fraction (first order)
F2 = 1-F1 ; CENTRAL fraction (zero order)
ALAG2 = THETA(2) ; Lag on slower z.o. process; h
D2 = THETA(3) ; DURATION Z.O.; h
KA = THETA(4) ; First-order absorption; 1/h
TVV2 = THETA(5)
V2 = TVV2*EXP(ETA(1)) ; Central CMT volume; L
TVK = THETA(6)
K = TVK*EXP(ETA(2)) ; F.O. elimination rate; 1/h
S2 = V2/1000 ; DOSE = mg; DV = ng/mL$ERROR
IPRED = F
Y = F*(1+EPS(1))$THETA
(0, 0.3, 1) ; First-order fraction of the dose
(0, 2) ; Lag for z.o. absorption: h
(0, 8) ; Duration of z.o. absorption
(0, 0.35) ; First-order absorption rate: 1/h
(0, 50) ; Volume of distribution: L
(0, 0.085) ; First-order elimination rate constant: 1/h$OMEGA
0.08
0.08
$SIGMA
0.04
$ESTIM … ; Add other code as needed
$TABLE …
9.4.4 Parallel First-Order Absorption Processes, without Defined Fractions
A similar situation, but one that changes the coding approach, arises when the two input processes are both first order. In this case, two compartments are needed that can transfer drug by first-order rates of transfer into the central compartment. There is no specific ADVAN that includes this possibility, so one must use one of the general ADVANs and code the structure of the model in the control file. If all transfers in the entire model are first order, then we can use one of the general linear model subroutines (ADVAN5 or ADVAN7).
The dataset for this scenario with two parallel first-order absorption processes must have a dose record into each depot compartment for each administered dose. Since both absorption processes are parallel first-order processes, the RATE data item is not needed, but like the example in Section 9.4.3, the AMT variable should equal the total administered dose amount. Example dosing records for the first subject are shown in Table 9.3.
Table 9.3 Example dosing records for parallel absorption processes, with estimated amounts absorbed through each route
| ID | TIME | DV | AMT | EVID | MDV | CMT |
| 1 | 0 | . | 300 | 1 | 1 | 1 |
| 1 | 0 | . | 300 | 1 | 1 | 2 |
Assuming two first-order absorption rate processes, this model can be implemented with the following code using a general linear model expression (ADVAN5 or ADVAN7):
$PROBLEM Parallel first-order absorption
$INPUT ID TIME DV AMT EVID MDV CMT
$DATA filename
$SUBROUTINE ADVAN5
$MODEL
COMP (DEPOT1, DEFDOS)
COMP (DEPOT2)
COMP (CENTRAL, DEFOBS)
$PK
F1 = THETA(1)
F2 = 1 – F1
ALAG2 = THETA(2) ; Lag on slower process
K13 = THETA(3) ; DEPOT1 -> CENTRAL
K23 = THETA(4) ; DEPOT2 -> CENTRAL
TVV3 = THETA(5)
V3 = TVV3*EXP(ETA(1)) ; Central CMT volume
TVK = THETA(6)
K30 = TVK*EXP(ETA(2)) ; First-order elim. rate
S3 = V3/1000 ; DOSE = mg; DV = ng/mL
$ERROR
Y = F * (1 + EPS(1))
$THETA … ; Add other code as needed
$OMEGA … ;
$SIGMA … ;
$ESTIM … ;
$TABLE … ;
This example is also similar to the scenario in Figure 9.1, except both absorption processes are first order. With two parallel first-order absorption steps, the model cannot be described using a specific ADVAN, and one of the general linear (link models) or nonlinear (differential equation models) ADVANs must be used.
9.4.5 Zero-Order Input into the Depot Compartment
A final model structure we will mention with these sorts of mixed rate absorption processes is one that has a zero-order input into the depot compartment. This is simply an infusion of the drug into the depot, which is then absorbed by a first-order process. This model has some nice properties, giving a sigmoidal shape to the absorption profile. The approach has certain advantages over a simple first-order absorption model with lag time. Frequently, the inclusion of lag time parameters can lead to numerical difficulties during estimation. The infusion of drug into the depot can sometimes avoid these numerical issues. With this model structure, the entire dose goes through both input processes, the zero order, followed by the first order. There is only one dose record needed per actual dose administered, that being the infusion dose into the depot. The dose record can have RATE = –2 and the duration of input estimated in the control file with a fixed-effect parameter. Since there is only one dosing record used and the entire dose goes through both input steps, there is no need to divide the dose into separate fractions through each route as with some of the models described earlier.
There are many other drug absorption models that can be constructed, including the transit compartment models, mechanistic absorption models, enterohepatic recycling models, Weibull function models, and many others. Each of these can be expressed in NONMEM using user-written models that extend the properties available in the specific ADVANs. The flexibility of model expression in NONMEM has hopefully been illustrated in this series of absorption models, along with some of the specific coding features of the datasets and control stream code that are needed to implement these models.
9.4.6 Parent and Metabolite Model: Differential Equations
For a more complex modeling scenario, consider that a drug compound in development is eliminated both renally and by a saturable metabolic process to a single metabolite. Suppose a 100-mg single dose of the parent compound is administered orally, and concentration data are collected for both the parent compound and the metabolite. Simultaneous description of the concentrations of the parent and metabolite for this nonlinear model requires the expression of the model using differential equations. The model is illustrated in Figure 9.6, where MPR is the metabolite-to-parent ratio of molecular weights, ka is the first-order absorption rate, and k20 and k30 are the first-order elimination rates for the parent and metabolite, respectively. A(1) is the amount of parent compound in the central compartment at time, t. Saturable elimination is defined via the Michaelis–Menten model parameters Vmax, the maximum rate of elimination, and km, the second compartment amount (A(2)) at which the metabolism rate is half maximal. Differential equations to define the model in terms of rates of change in compartment amounts are listed below: