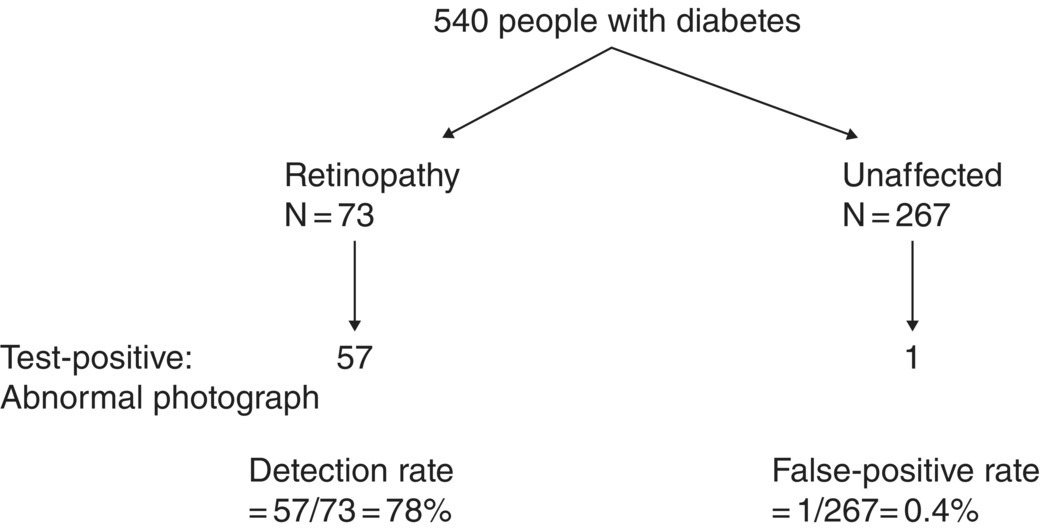
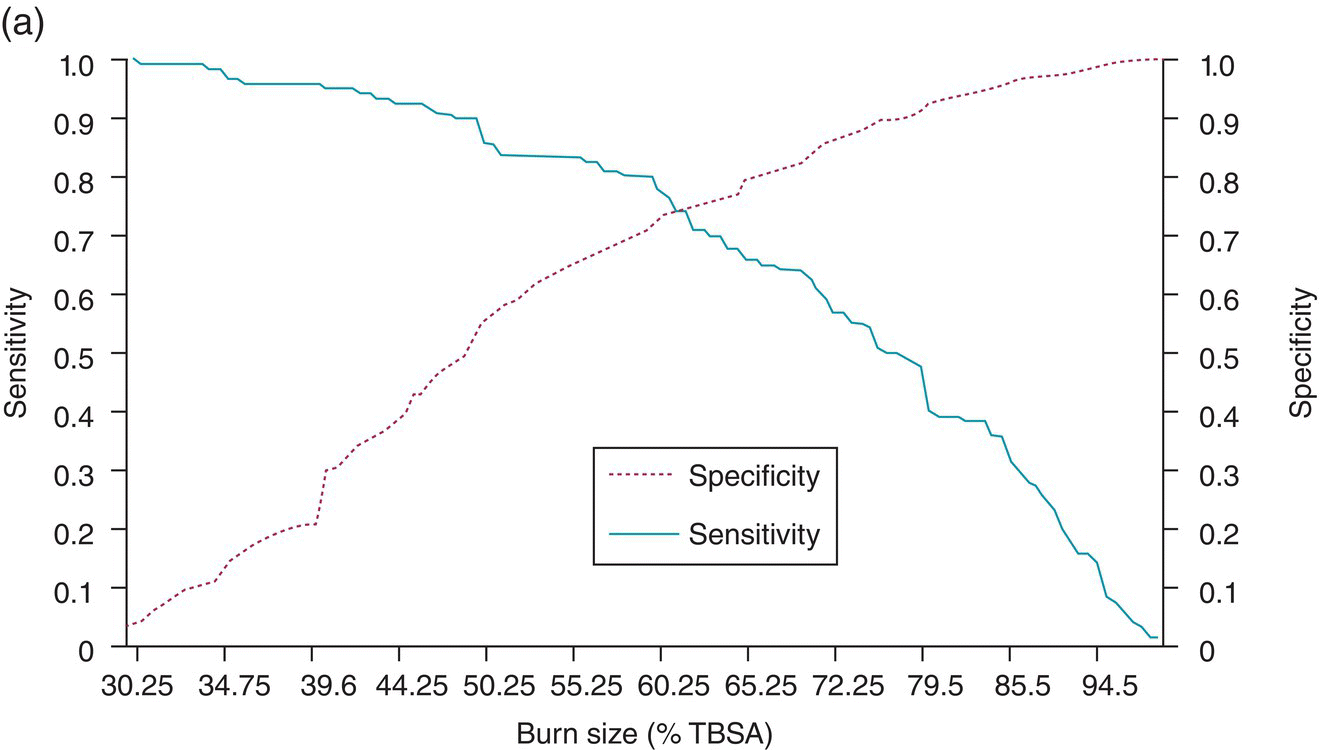
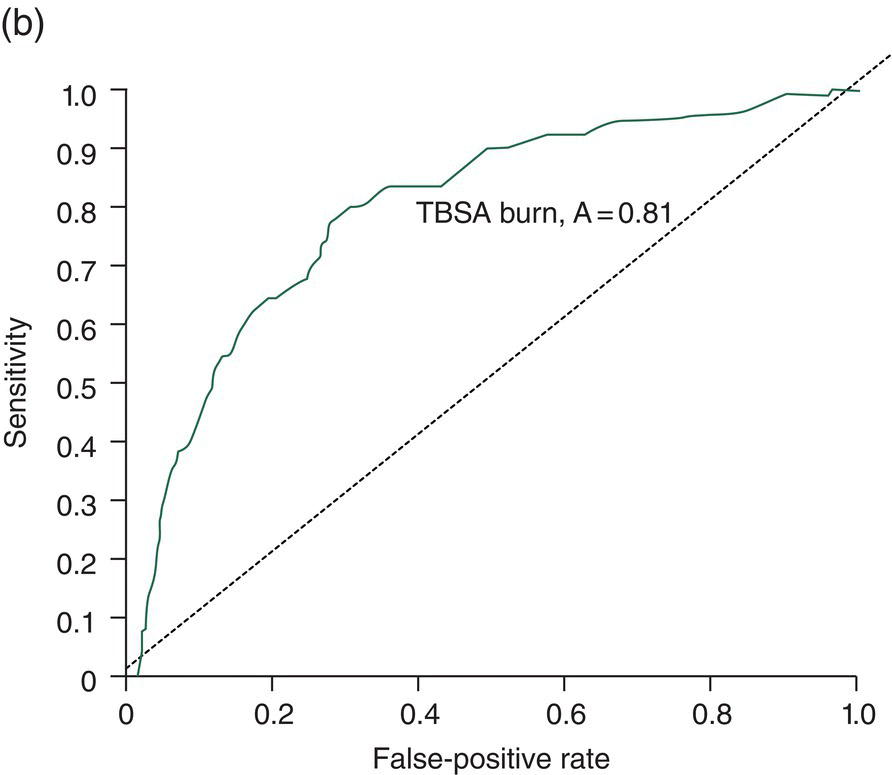
Chapter 9 Many observational studies aim to examine the association between an exposure and outcome. A special case of this is to develop a model using various characteristics to predict whether someone is likely to have or develop a specified outcome or not. Prognostic marker research involves some of the analytical methods used in previous chapters, but there are additional concepts. The approaches covered in this chapter can be used to examine screening and diagnostic tests. Studies using genetic prognostic markers are becoming increasingly common, and these also have some special considerations. The main purpose of a prognostic marker or model (the exposure) is to try to predict the outcome for an individual.1 The marker could be a simple features such as age and gender, a clinical measurement such as blood pressure, imaging markers (from X-rays, MRI, or CT scans), or a biological marker or genetic factor measured in the blood, urine, or tissue. (All types of these markers are used as examples in this chapter.) The outcome could be the occurrence of a new disorder in an unaffected person, disease progression or death for a person who is already ill, or any well-defined change in health status. In practice, only diagnostic markers (or tests) are designed to show whether or not an individual will have a specific outcome (with almost complete certainty), so prognostic markers and models essentially estimate the risk (chance) of the outcome. The clinical value of a good prognostic factor is that it can identify people (or patients) who are likely to benefit from an intervention, and thus prevent an adverse outcome, or it identifies people appropriate for a diagnostic test, which is too harmful or expensive to give to everyone. Several aspects (Box 9.1) need to be considered when proposing a prognostic marker (or model), in addition to the quantitative measures that are described in the following sections. More details are provided in a BMJ series [1–4] and elsewhere [5–7]. Prognostic markers can be examined using the designs covered in Chapters 5–7. The preferred design is a cohort study, ideally prospective, although retrospective studies could be acceptable (acknowledging issues over missing data). This is because absolute risk, given the marker result, can be estimated in a cohort study, but it is not possible to do this in a case–control study, where the number of cases and controls is chosen by the researcher. However, it is possible to obtain information on prognostic performance from a case–control study (e.g. by mathematical modelling) and apply it to the background risk for a disorder. This needs to be done carefully, ensuring that both the cases and controls come from the target population of interest. Other types of studies include those based on patient records, which are likely to have issues over missing data, and quality of data, so the conclusions of these are often to recommend further prospective studies to confirm the findings. There are two useful statistical considerations when examining prognostic markers: effect sizes and prognostic performance. Effect sizes are measures of association, such as relative risk and odds or hazard ratio (Chapter 3). They indicate whether the relationship between a marker and a disorder is small, moderate or large. Many researchers only provide effect sizes when they report prognostic studies, which is the first step, but these do not really tell us how good a prognostic marker is at forecasting outcomes. Both measures are ultimately required. Prognostic performance is examined using two quantitative parameters: detection rate (DR, also called sensitivity or true positive rate) and false-positive rate (FPR, which is 1 − specificity). These are illustrated in Figure 9.1. Figure 9.1 Illustration of measures of prognostic performance using a study of people with insulin-dependent diabetes, in which the prognostic marker (or screening test) is a retinal photograph of the eye (abnormal or normal). The sensitivity is also 78%, and the specificity would be 99.6% (1 − FPR). Unlike effect sizes, which are calculated by analysing all individuals together, DR and FPR always consider them as two separate groups: people with the outcome (affected) and those without (unaffected). It is important to have both the DR and FPR. A high DR (e.g. 85%) is meaningless without knowing whether the FPR is low or high (e.g. 5 or 50%). A diagnostic marker or test should have a DR close to 100% and FPR close to 0%. There is no gold standard for what makes a good prognostic marker, in terms of size of DR and FPR. Figure 9.1 shows an excellent marker (high DR and very low FPR), but many other markers have lower DRs (50–70%) and higher FPRs (e.g. 5–20%). Marker performance can be considered in relation to the seriousness of the disorder, and what happens to people who have positive test results. For example, markers for predicting Down’s syndrome in pregnancy have a DR of 70–85%, but this comes from specifying a low FPR (< 5%), because women who are test positive are offered an invasive and expensive diagnostic test (e.g. amniocentesis), which has a risk of miscarriage. In contrast, mean corpuscular haemoglobin is used to screen for β-thalassaemia in pregnancy and because the aim is to detect almost all cases (DR close to 100%), the FPR can be relatively high (up to 37%) The subsequent test is only another blood (diagnostic) test that, although relatively expensive, is not harmful. The most commonly used terms in the literature are sensitivity and specificity, although DR is a better term than sensitivity, which has other definitions in medicine (e.g. lower limit of assay measurement). FPR is more relevant than specificity, because it designates the individuals who go on to have further investigations and/or interventions. DR and FPR can be combined to produce a likelihood ratio (LR = DR/FPR), which is a way of quantifying the ‘power’ of the marker. LR = 1 is a useless marker. The larger the value, the higher the DR in relation to the FPR (e.g. a good marker would have DR = 80% and FPR = 5%, which produces a large LR of 16). Two characteristics of prognostic markers or models are worth noting: Although DR and FPR are important parameters, it is also necessary to see how well the marker works in the population of interest. This is achieved by examining the odds of being affected given a positive result (OAPR) or positive predictive value (PPV); see example 9.1 (page 177). When several prognostic markers are examined together, they should be combined into a model using multivariable linear, logistic, or Cox regressions depending on whether the outcome measure involves ‘taking measurements on people’, ‘counting people’, or measuring the time until an event occurs. Effect sizes such as relative risk, odds ratio, and hazard ratio measure the relationship between an exposure (prognostic marker) and outcome. This is conceptually different from the prognostic performance of the marker, which examines how well it predicts the outcome. It is not commonly recognised that a prognostic marker needs to be very strongly associated with the disorder (i.e. high or low odds or hazard ratios) to have a good performance [8]. For example, maternal serum alpha-fetoprotein (AFP) is a prognostic marker for neural tube defects in pregnancy (and used for prenatal screening). The odds ratio between the highest and lowest quintile of AFP is 246 (a very large effect), and the corresponding DR = 91% and FPR = 5% indicates good performance. In comparison, although the association between serum cholesterol and ischaemic heart disease is established and appears to be a large effect (odds ratio of 2.7 between the highest and lowest quintiles among UK men), the DR is only 15% for a FPR of 5%; that is, cholesterol is not an effective prognostic marker, because it has a poor performance [8]. Having a moderate or reasonably strong association does not necessarily mean that the marker is good at predicting outcomes. When using a single prognostic marker, one dataset is often sufficient when the cut-points used to estimate DR and FPR are already pre-established and have not been developed by the researchers. For example, in Figure 9.1, the retinal photograph can only be normal or abnormal, and for a continuous marker like blood pressure, fixed values such as ≥ 120, ≥ 130, ≥ 140 mmHg, etc. can be used. Neither of these is driven by the actual dataset. However, if there is uncertainty over the generalisability of the study findings, then it might be appropriate to examine the marker in another (independent) dataset. When examining several prognostic markers, each will probably have different units of measurement, so they need to be combined to produce a single measure, and then a cut-off point can be applied, as if dealing with a single marker. This combined measure and cut-off point come from a statistical model, and the model needs to be developed by the researchers. This could be done using a large study that is split into two, or two separate studies of similar individuals, so that the prognostic model is developed with one dataset (training dataset) and tested on another (validation dataset). Using the same dataset to both develop and test the model will give biased (optimistic) estimates of performance. The validation dataset can also be used to check whether the model is sufficiently reliable by comparing estimated (predicted) with observed risk values. Splitting a dataset (half training and half validation or, two-thirds training and one-third validation) could be performed randomly, but then the two groups should be similar to each other, and this could overestimate prognostic performance. It is better to split the dataset using time (e.g. the first two-thirds of registered participants in the study form the training set, and the last third make up the validation set). This has the advantage of attempting to validate the model prospectively, which is similar to what would be done in practice (i.e. a model developed now, to be applied to future individuals). The number of events is as important as study size, so it may be better to divide the data according to events (see Example 3), to ensure that sufficient numbers of events occur in each dataset to produce reliable results. Having a completely independent dataset (as the validation data) is ideal because it will address generalisability, but it can often be difficult to find one that has similar individuals to the one used to develop the model and that has all the factors measured. Other methods are cross-validation or bootstrapping (especially if the dataset is not large enough to be split). With cross-validation, one individual is removed, and the model is developed using the remaining individuals and then tested/validated on the removed individual, who is classified as marker positive or not. This is repeated for every individual in the dataset, and DR and FPR are obtained by counting the number of positives in the affected and unaffected groups. With bootstrapping, if there are, for example, 435 individuals in the study, a random sample of 435 is selected, after replacing each person (so an individual could be included several times in the sample or not at all). The model is developed on this sample and then tested on the original dataset. The process is repeated at least 100 times, with the average model performance estimated. Another approach involves using the dataset to produce statistical parameters (e.g. means, standard deviations and correlation coefficients), that are incorporated into a model which produces DR, FPR and OAPR [9]. An advantage of these methods, over splitting the dataset, is that all of the data values are used to develop and test the model. Prognostic markers are often examined as part of translational sub-studies within an observational study that is already established (completed or ongoing). Therefore, an estimation of the sample size can be made to only check whether the study is large enough for the marker analysis. A simple sample size for DR or FPR can be established by specifying the width of the 95% confidence intervals (CIs) that would be considered sufficiently narrow. This will depend on what is feasible and will involve guessing what the DRs and FPRs are likely to be. Table 9.1 illustrates this. Small sample sizes give wide intervals, and if researchers intend for the interval around either the DR or FPR to be fairly narrow, then large numbers are needed. A noticeable gain occurs in increasing the sample size from 50 to 200, but not from 400 to 1000. Table 9.1 95% CIs for varying DR (sensitivity) and FPR (1-specificity), according to the number of individuals available for each measure. For example, if DR = 60%, p = 0.60 and standard error (SE) is 95% CI is p ± 1.96 × SE. When considering the sample size of a training dataset used for several prognostic markers examined together, there are no standard sample size methods for multivariable regression analysis. It is recommended that there should be at least 10 events per included marker [10]. If there are eight factors, therefore, ≥ 80 events are required, and the researchers must then scale up to the number of participants needed to achieve this. For a single prognostic marker, only one sample size estimation may be needed, but for several markers, which involve separate training and validation datasets, a sample size could be calculated for each. In the two examples below, the outcome is either a disorder (affected or unaffected) or mortality (dead or alive). Both are based on a single prognostic marker and so may only require a single dataset (not separate training and validation datasets), because the definition of marker positive is pre-defined. Table 9.2 Findings from a study examining the performance of a prognostic marker (skull X-ray) in predicting the presence or absence of a cranial haematoma in patients with a head injury. DR, detection rate; FPR, false-positive rate; LR, likelihood ratio; DR ÷ FPR. Odds ratio: odds of having a haematoma in those with a fracture compared with those without a fracture. DR for haematoma is found from the number with a fracture/the total in the column (e.g. 65% = 55/84). Similarly for FPR (1% = 1721 / 175, 207). The absolute risk for having a haematoma is the number affected divided by the total in the row. For example, 3.1% is 55/(55 + 1721), or expressed as an odds, it is 55:1721, which simplifies to 1:31 (called OAPR). NB: The table illustrates what all prognostic markers do: they change a person’s risk. Before the patients with a head injury, who were not disorientated, had an X-ray, their risk was 0.05% (the background or overall risk). After the marker result is known, the risk either reduces (to 0.02% for marker negative patients, no skull fracture) or increases (to 3.1% for marker-positive patients, with skull fracture). The risk in the marker-positive group is sometimes called PPV, or OAPR. For patients who are not disorientated, the odds ratio for having a haematoma (skull fracture vs. no fracture) is 191. The corresponding relative risk is 185 (55/55 + 1721 ÷ 29/29 + 173486), close to the OR. This is a huge effect (strong association), which has a good prognostic performance: DR = 65% (65% of those with a haematoma had a skull fracture) and FPR = 1% (only 1% of those without a haematoma had a skull fracture). The OAPR is the risk of having the disorder (here, a haematoma) only among those who are marker positive (here, skull fracture). It is 1:31 (or absolute risk of 3.1%, PPV). This means that to detect one affected case, 31 patients without a haematoma need to be followed up and investigated (hospital admissions and CT scans) unnecessarily. (Alternatively, only 3.1% of orientated people with a skull fracture have a haematoma.) Therefore, although this marker itself has a strong association with having a haematoma it is not very efficient when used to predict a haematoma in a population. The problem is not the marker; it is the low incidence of haematoma in people who are not disoriented (only 0.05% or 1 in 2000). In those who are disoriented, the association between the marker and disorder is more modest (odds ratio 35) but still represents a large effect. The DR increases to 77%, but the FPR is much larger (9% instead of 1%). Skull X-rays therefore appear initially as a less effective prognostic marker in these particular patients (LR = 8.5), but the OAPR is 1:3 (357:1214 or absolute risk 22.7%). (Alternatively, 22.7% of disorientated people with a skull fracture have a haematoma.) This means that there would only be three unnecessary additional investigations in people without a haematoma in order to detect one affected case. Even though the marker (skull X-ray) seems to have a lower prognostic performance in these patients than those who are not disorientated, when applied to the population, it becomes worthwhile because of the higher background incidence (1 in 30, 461/13, 680)). This example shows the importance of not only looking at prognostic performance (DR and FPR), but also how well the marker works in a population (OAPR, or absolute risk). The adjusted OR is important because it has allowed for potential confounding factors, so burn size seems to be an independent risk factor. The OR for dying among patients with a burn size of ≥ 60% (compared with burn size <60%) is high: 10.07 (95% CI 5.56–19.22), after allowing for other factors (inhalation injury, gender, age at admission, and time from the burn injury to admission). The adjusted or is best to use: burn size seems to be an independent risk factor. Figure 9.2a shows how DR (sensitivity) and FPR (1 − specificity) change as the burn size cut-off increases from 30.25% up to almost 100%. Using markers of the type used in Example 9.1, in which the result can only take one of two levels (normal or abnormal), it is not possible to change the DR or FPR. However, with a continuous marker, such as burn size, it is possible to change prognostic performance. As the DR increases, so too does the FPR. A receiver operating characteristic (ROC) curve is commonly shown for this type of prognostic marker (Figure 9.2b), and a quantitative measure of performance is the area under the curve (AUC), also known as the concordance index (‘c’). The AUC value is the chance that the marker will produce a higher risk value for an individual with the outcome than someone without the outcome. If the marker is useless, DR and FPR are the same, as indicated by the line of identity in Figure 9.2b; the AUC would be 0.5 (i.e. the area for the whole square plot is 1.0, and the line of identity represents half of this). The higher the AUC, the better the prognostic marker. In the example, the AUC is 0.81, which is acceptable. Figure 9.2 DR (sensitivity) and FPR (1 − specificity) in relation to burn size (% of TBSA). The lower diagram is a plot of DR against FPR, called an ROC curve, from which the AUC (A) is 0.81. Both diagrams can be used to develop Table 9.3. Source: Kraft et al., 2012 [12]. Reproduced by permission of Elsevier.
Prognostic markers for predicting outcomes
9.1 Prognostic markers and models
9.2 Study design
Measuring prognostic performance
Training and validation datasets (examining several markers)
9.3 Sample size
Sample size used for either DR or FPR
N = 50
N = 200
N = 400
N = 1000
DR (%)
60
46–73
53–67
55–65
57–63
70
57–83
64–76
66–74
67–73
80
69–91
74–85
76–84
77–82
90
82–98
86–94
87–92
88–92
FPR (%)
5
0–11
2–8
3–7
4–6
10
2–18
6–14
7–13
8–12
15
5–25
10–20
11–18
13–17
20
9–31
14–25
16–24
17–22
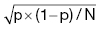 .
.
9.4 Analysing data and interpreting results
Outcome measures based on ‘counting people’ (binary or categorical endpoints)
Not disorientated
Disorientated
Haematoma
Unaffected
Absolute risk (%)
Haematoma
Unaffected
Absolute risk (%)
Fracture
55
1,721
3.1 (ppv)
357
1,214
22.7 (ppv)
No fracture
29
173,486
0.02
104
12,466
0.83
Total
84
175,207
0.05
461
13,680
3.3
DR = 65%
FPR = 1%
DR = 77%
FPR = 9%
LR = 65
LR = 8.5
Odds ratio (95% CI)
191 (122–300)
35 (28–44)
Disorder: cranial haematoma.
Prognostic marker: skull X-ray.
Marker (test) positive: skull fracture.
What happens to ‘positives’: further investigations, such as CT scan after hospital admission.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


