Principles of Cellular Excitability and Electrochemical Transmission

Elizabeth Mayne, Lauren K. Buhl, and Gary R. Strichartz

   INTRODUCTION

Cellular communication is essential for the effective functioning of any complex multicellular organism. The major mode of intercellular communication is the transmission of chemical signals, such as neurotransmitters, neuropeptides, and hormones. In excitable tissues, such as nerves and muscles, rapid intracellular communication relies on the propagation of electrical signals—action potentials—along the plasma membrane of the cell. Both chemical and electrical transmission commonly involve the movement of ions across the plasma membrane or across the membranes of internal organelles such as the endoplasmic reticulum. Ionic movements can directly change the cytoplasmic concentration of ions, such as Ca²⁺, that are key regulators of biochemical and physiologic processes like phosphorylation, secretion, and contraction. Ionic movements also change the electrical potential across the membrane through which the ions flow, thus regulating various voltage-dependent functions including the opening of other ion channels. Some of these events are brief, with durations and actions of several milliseconds (0.001 sec). Others can take many seconds, with biochemical consequences—for example, phosphorylation of proteins—that can persist for minutes or hours. Even gene expression can be regulated by changes in ion concentrations, resulting in long-term changes in cellular physiology, growth, differentiation, and death.

Many drugs modify chemical or electrical signaling to increase or decrease cellular excitability and electrochemical transmission. To appreciate how such drugs act, the present chapter explains the electrochemical foundations that underlie signaling within and between electrically active cells. These general principles are applicable to many areas of pharmacology, including those discussed in Chapters 10 to 12 (Section IIB, Principles of Autonomic and Peripheral Nervous System Pharmacology), Chapters 13 to 19 (Section IIC, Principles of Central Nervous System Pharmacology), and Chapter 24, Pharmacology of Cardiac Rhythm.

   CELLULAR EXCITABILITY

Excitability refers to the ability of a cell to generate and propagate electrical action potentials. Neuronal, cardiac, smooth muscle, skeletal muscle, and many endocrine cells have an excitable character. Action potentials may propagate over large distances, as in peripheral nerve axons that conduct over several meters, or they may stimulate activity in cells of much smaller size such as the 30- to 50-μm-diameter interneurons that are contained within a single autonomic ganglion. The function of action potentials differs depending on the cell in which they occur. Propagating waves of action potentials rapidly conduct encoded information with fidelity over long distances along axons. Within a small cell, action potentials excite the whole cell at once, causing an increase in intracellular ions (e.g., Ca²⁺) followed by a rapid release of chemical transmitter molecules or hormones. These chemicals then travel to specific receptors, near or far from the releasing cell, to effect chemical transmission, which is discussed in the second part of this chapter.

Cellular excitability is fundamentally an electrical event. Therefore, an understanding of basic electricity is necessary to explain the biological processes of excitability and synaptic transmission. The following sections present basic principles of electricity as applied to two important cellular components—the plasma membrane and ion-selective channels.

Ohm’s Law

The magnitude of a current (I, measured in amperes) flowing between two points is determined by the potential difference (V, measured in volts) between those two points and the resistance to current flow (R, measured in Ohms):

For example, current may flow from the extracellular to the intracellular compartment in response to an electrical potential difference (also known as a voltage difference) across the plasma membrane. Voltage can be thought of as a potential energy or as the propensity for charged particles to flow from one area to another. Resistance is the obstacle to this flow. Decreased resistance allows greater ion flow and therefore increased current (current has units of charge/time). When this relationship, known as Ohm’s law, is applied to biological membranes such as the plasma membrane, the electrical resistance is often replaced by its reciprocal, the conductance (g, measured in reciprocal ohms, or siemens [S]):

For simplicity, assume that all resistive elements in the cell membrane behave in an “ohmic way”; that is, their current–voltage (I-V) relationship is described by Equations 8-1a, b. In this case, the I-V relationship is linear, with a slope given by the conductance, g. Figure 8-1 represents the transmembrane current (I) measured at different transmembrane potentials (V ) in a hypothetical cell. The slope of the I-V curve equals the conductance. From a conceptual perspective, current increases as voltage increases because a higher voltage results in a greater potential energy difference between the inside and outside of the cell, which in turn favors an increased rate of charge movement across the membrane.

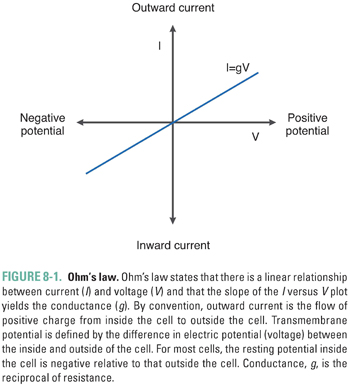
The convention used in most texts and in this chapter is that the voltage across a membrane, the “membrane potential,” is expressed as the difference between the intracellular and extracellular potentials (V_m = V_in − V_out). For most normal cells, V_m is negative when the cell is at rest (V_in < V_out). The membrane is termed hyperpolarized when V_m is more negative than at rest, and it is described as depolarized when V_m is more positive than at rest. Current is conventionally defined with respect to the direction in which positive charge flows. Positive charge moving from inside to outside is called outward current and is represented graphically by positive values. Positive charge moving from outside to inside is called inward current and is represented graphically by negative values. Movement of negative charge is defined in the exact opposite way. Note that an efflux of K⁺ cations is electrically equivalent to an influx of Cl⁻ anions; both are outward currents.

Ion Channels

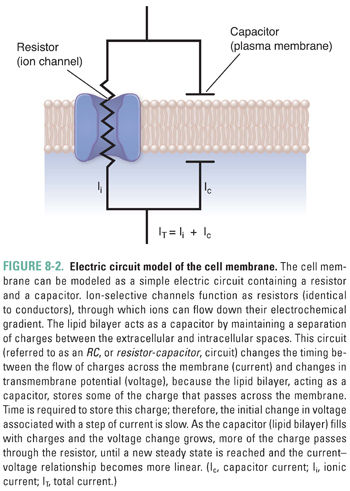
How does current actually flow across a cell membrane? Biological membranes are composed of a lipid bilayer within which some proteins are embedded and to which other proteins are attached (schematically represented in Fig. 8-2). Pure lipid membranes are virtually impermeable to most polar or charged substances, thus having a very high intrinsic resistance. From an electrical perspective, the lipid bilayer also acts as a capacitor by separating the extracellular and intracellular ions. To enable the passage of ions that carry electrical current, ion channels span the membrane. Most ion channels are gated—that is, they remain closed until specific signals dictate their opening. Once open, they exhibit ion selectivity, allowing only certain ions or types of ions to pass. From an electrical perspective, a set of gated ion channels is a variable conductor: it provides many individual conductances for different ions to flow between the extracellular and intracellular environments. The magnitude of the overall conductance depends on the fraction of channels in the open state and the conductance of the individual open channels.

Channel Selectivity, the Nernst Equation, and the Resting Potential

By itself, the hypothetical I-V relation in Figure 8-1 does not explain the electrical behavior of most real cells. If a cell behaved according to Equation 8-1, then the potential difference across the membrane would be zero in the absence of an externally applied current. Instead, most cells maintain a negative potential difference across their plasma membrane. This voltage difference is most pronounced in neuronal and cardiac ventricular cells, where a resting potential (the voltage difference across the membrane in the absence of external stimuli) of −60 to −90 mV can be recorded. The resting potential results from three factors: (1) an unequal distribution of positive and negative charges on each side of the plasma membrane, (2) a difference in selective permeabilities of the membrane to the various cations and anions, and (3) the current-generating action of active (energy-requiring) and passive pumps that help to maintain the ion gradients. The effects of these interrelated factors can be explained best with an example.

Consider the case when there are only potassium ions (K⁺) and protein-bound anions (A⁻) inside the cell and no other ions outside the cell (Fig. 8-3). If this cell’s membrane is permeable to potassium alone, due to the presence of channels that are open at rest and pass only K⁺ ions, then K⁺ will flow outward, while A⁻ will remain inside. The K⁺ ions flow outward because of a chemical gradient; that is, K⁺ efflux is energetically favorable because the K⁺ concentration inside the cell is greater than that outside the cell. A potential efflux of the anion, A⁻, is also favored by its chemical gradient, but the absence of transmembrane channels permeable to A⁻ prevents this anion from flowing across the membrane. Because of this selective permeability for K⁺, every K⁺ ion that exits the cell leaves one net negative charge (an A⁻ ion) on the inside of the cell and adds one net positive charge (a K⁺ ion) on the outside of the cell. This separation of charges across the membrane creates a negative membrane potential.

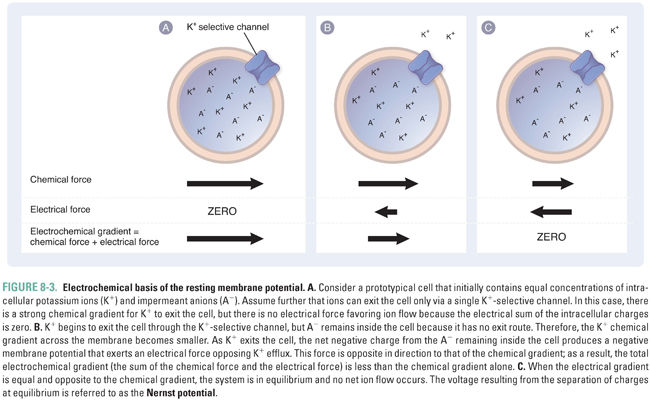
If a negative membrane potential were not established as K⁺ leaves the cell, then K⁺ ions would continue to exit until the extracellular concentration of K⁺ was equal to the intracellular concentration of K⁺. However, the establishment of a voltage difference creates an electrostatic force that eventually prevents net K⁺ efflux (Fig. 8-3B). Thus, the electrical gradient (V_m) and the chemical gradient “pull” the K⁺ ions in opposite directions: the electrical gradient favors an inward flow of K⁺ ions, while the chemical gradient favors an outward flow of K⁺ ions. These forces combine to create an electrochemical gradient, which is equal to the sum of the electrical gradient and the chemical gradient. The transmembrane electrochemical gradient is the net driving force for passive ion movement across biological membranes.

As a result of the electrochemical gradient, the extracellular concentration of K⁺ does not equalize with the intracellular concentration. Instead, an equilibrium is established in which the electrostatic force “pulling” K⁺ back into the cell is balanced exactly by the chemical gradient driving K⁺ efflux. The electrical potential at which this equilibrium occurs, for any permeant ion X, is a function of the charge of the ion (z), the temperature (T), and the intracellular and extracellular concentrations of the ion. This relationship is expressed as the Nernst equation:

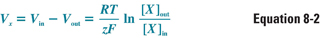
where V_x is the transmembrane potential that a membrane selectively permeable to ion X would reach at equilibrium (i.e., the Nernst potential for that ion), V_in − V_out is the transmembrane voltage difference, RT/zF is a constant for a given temperature and charge (this number simplifies to 26.7 mV for a charge of +1 at a temperature of 37°C), and [X]_out and [X]_in are the extracellular and intracellular concentrations, respectively, of ion X. The electrochemical driving force on ion X is equal to the difference between the actual membrane potential and the Nernst potential for that ion, V_m − V_x.

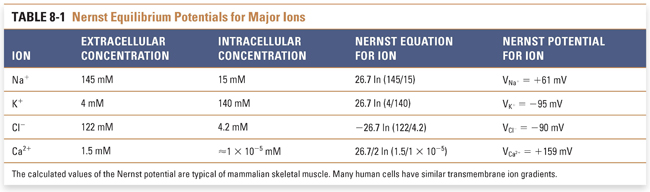
The third determinant of the resting membrane potential is the active and passive ion pumps that move ions across the membrane. These pumps govern the concentration of ions inside and outside the cell and act as generators of net current by moving net charge across the membrane, termed electrogenic transport. Numerous pumps play an important physiologic role in maintaining ion gradients; these include the ATP-dependent Na⁺/K⁺ pump (which uses the energy of ATP hydrolysis to extrude three Na⁺ ions for every two K⁺ ions that enter the cell) and the Na⁺/Ca²⁺ exchanger (which extrudes one Ca²⁺ for every three Na⁺ ions that enter the cell). The coordinated action of these pumps closely regulates the intracellular and extracellular concentrations of all biologically important cations and anions. By knowing the values of these ion concentrations, it is possible to calculate the Nernst potentials for these cations and anions at physiologic temperature and, hence, the value of the transmembrane potential at which the net driving force for each ion is equal to zero (Table 8-1).

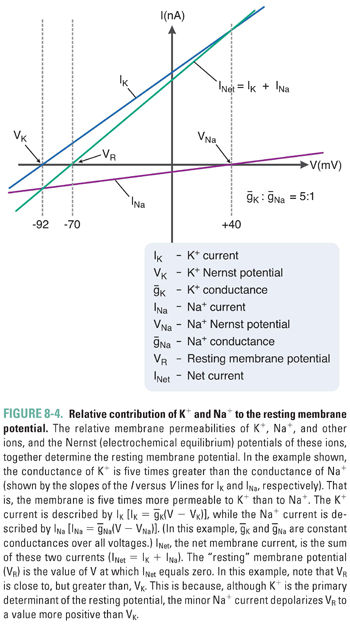
Variations in the magnitude and direction of transport for each ion (mediated by pumps and exchangers in the plasma membrane) and differences in the membrane permeability for each ion (mediated by channels selective for each ionic species) generate the distinct intracellular and extracellular concentrations for each of the four key ions. The relative ionic permeabilities of the neuronal membrane at rest are K⁺ >> Cl⁻ > Na⁺ >> Ca²⁺. Because the plasma membrane contains K⁺-selective channels that are open under resting conditions while most other channels are closed, the resting membrane potential most closely approximates the Nernst potential for K⁺ (about −90 mV). In reality, the additional, weak permeabilities of other ionic species raise the resting membrane potential above that for K⁺. Thus, although K⁺ is the most permeant ion, the permeability of the other ions and the action of the “electrogenic” pumps also contribute to the overall resting potential. At the steady state that describes the true resting membrane potential (Fig. 8-4), V_m does not equal the Nernst potential for any of the individual ions, and each ionic species experiences a net electrochemical force. In other words, (V_m − V_ion) is nonzero, and small ion fluxes occur. The algebraic sum of these inward and outward currents is small and is balanced by currents from active, electrogenic pumps, so there is no net current across the resting membrane. It has been estimated that up to 25% of all cellular energy in excitable tissues is expended in maintaining ion gradients across cellular membranes.

Stay updated, free articles. Join our Telegram channel

Join