Chapter Two Natural philosophy
CHECK YOUR EXISTING KNOWLEDGE
Introduction
The principal tributary to which the river of modern science can be traced is probably Roger Bacon (?1214–?1292), a Somerset-born Franciscan friar, philosopher, alchemist and medic; the ‘Father of Science’, ‘Dr Miribalis’ (Fig. 2.1). In his most famous work, Opus Maius, he outlined his unsurpassed knowledge of gunpowder, optics, mathematics, moral philosophy, theology, grammar…and experimental science, of which he was probably the inventor and certainly an ardent practitioner.
It is Bacon who is credited with having invented the ‘Scientific Method’ – hypothesis tested by experimentation and observation. This may now seem basic in the extreme but, before Bacon, science was a matter of metaphysical debate and religious dogma; he sowed the seeds from which sprang the randomized controlled trials in today’s biomedical journals.
Velocity, angular velocity and acceleration
In everyday speech, ‘velocity’ and ‘speed’ are interchangeable; in physics, they are (usually) not. Both are measured in units of distance (displacement) per unit time (metres per second; miles per hour etc.); however, velocity is a vector quantity (having magnitude and direction) whilst speed is scalar (having magnitude alone).
In terms of graphical representation (Fig. 2.2), if time (t) is plotted on the x-axis and displacement (s) on the y-axis, then the slope of the graph represents the velocity: the change in displacement, Δs, divided by the change in time Δt. Whereas this is straightforward if the graph is a straight line (i.e. constant velocity). If it is not, then the mean velocity needs to be obtained using a method of calculation known as calculus. If you are unfamiliar with this, read the Fact File below before proceeding; if calculus is old hat, then you will easily appreciate that velocity can be written as:
This, for example, is why the Earth is accelerating around the sun, although its speed is constant (bar the loss due to friction of a millisecond per century), its velocity is constantly changing as it describes an ellipse around the sun. This can be inconvenient on occasions; however, if we measure displacement in terms of the number of degrees (θ) traversed per unit time we can measure the angular velocity (ω):
Mass and momentum
where g is the acceleration of free fall, which can vary depending on location (Table 2.1). Although we measure our weight in kilograms, it should in fact be measured in newtons; we can get away with it because we are in a (reasonably) constant gravitational field. If we were in free-fall or outer space, our weight would be 0 N, although our mass would be unchanged.
Table 2.1 Gravitational forces on selected astronomical bodies
| Body | Free fall acceleration |
|---|---|
| Earth | 9.8 ms−2 |
| Moon | 1.6 ms−2 |
| Jupiter | 25.3 ms−2 |
| Pluto | 0.6 ms−2 |
| Sun | 270.7 ms−2 |
| Neutron star | 1.4 × 1012 ms−2 |
Force
Once again, this is a term, the specificity of which, in physics, is in sharp contrast to the generality of meaning in the vernacular. To the scientist, force (F) is something that changes an object’s velocity, remembering that velocity is a vector quantity with both magnitude and direction. As we saw when discussing weight, force is measured in newtons (N) and can be calculated using the formula:
or, more concisely:
Newton’s laws and equations of motion
Reading this far, you will already have gathered that Sir Isaac Newton (Fig. 2.3) was an important man in the history of physics; arguably, he is the most important. Born in 1642, the year that Galileo died, Newton was something of a prodigy. Although he seems to have been a solitary, reclusive child, preferring introspection to classes (which probably bored him), he flourished whilst at Cambridge University; by the age of just 27, he was Lucasian Professor of Mathematics (the same chair is now held by Stephen Hawking). In 1665, when bubonic plague hit London and Cambridge, he withdrew to the family home in Lincolnshire and devoted himself to developing the ideas that would make him famous.

 CLINICAL FOCUS
CLINICAL FOCUS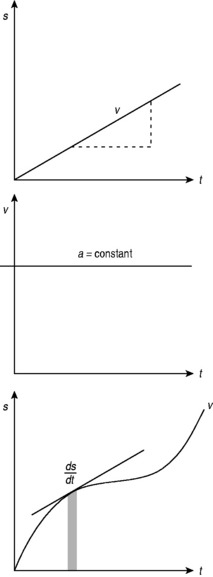
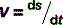
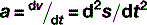
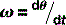
 Fact File
Fact File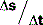 , which would refer to the gradient of the whole of a straight line, we write
, which would refer to the gradient of the whole of a straight line, we write 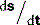 showing that we have worked out the gradient using calculus.
showing that we have worked out the gradient using calculus.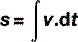
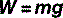
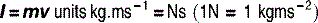
 CLINICAL FOCUS
CLINICAL FOCUS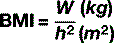
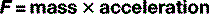
 DICTIONARY DEFINITION
DICTIONARY DEFINITION
 Fact File
Fact File CLINICAL FOCUS
CLINICAL FOCUS Fact File
Fact File


