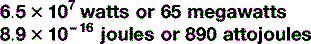Chapter One The tools of the trade
Check your existing knowledge
Weights and measures
Numbers
Numbers are also much more useful for mathematics than words. Organizing them into representations of units, tens, hundreds, thousands and having a ‘zero’ allows us to manipulate them arithmetically – see how easy you find the following sums:
(The answers are: a) ninety-three; b) XCIII and c) 93.)
Scientific notation
The digit to the top right is the number of times the main figure is multiplied together:
This convention also skirts around another problematical area, that of nomenclature. Although people are generally agreed as to the meanings of ‘hundred’, ‘thousand’ and ‘million’, thereafter American English diverges from its mother tongue and works in increments of a thousand rather than a million so, on one side of the Atlantic, a billion is a thousand million (109) and, on the other, it has traditionally been a million million (1012), except in some European countries, such as France, who have adopted the American convention. As the numbers get larger, so does the confusion: a British trillion (1018) is an American quintillion whilst an American trillion is a British billion. Because international finance uses the American convention, the trend is increasingly to follow this, even in the UK, but the use of scientific convention removes all ambiguity … as well as doing away with the need to remember how many noughts there are in a septillion! (For the record, in the US, 24; in the UK, 42.)
For numbers that aren’t exact multiples of ten, scientific notation uses multiplication so:
and
or
or
so
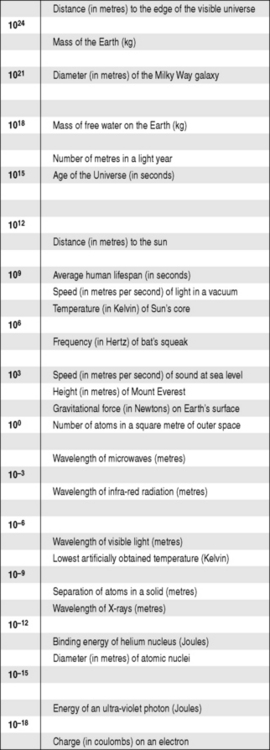
Now we have a way of representing any number, large or small, in a concise, consistent and comprehensible manner. This can take us from the unimaginably small to the incomprehensibly large (Fig. 1.1); however, bear in mind that the scale in this figure is not linear but logarithmic; that is, it rises in powers of ten: 106 is not twice as big as 103, it is one thousand times bigger. If we used a normal, linear scale, it wouldn’t just be a case being hard to fit Figure 1.1 on the page – it would be hard to fit into the known universe!
Units
As soon as commerce was invented, this definition lost its usefulness – as anyone familiar with the story of The King’s New Bed will know (a king kept having problems ordering a bed that he had measured as 6 feet long by 4 feet wide until he found a carpenter with feet the same size as his own; thereafter, he made models of his foot for his citizens to use for measurements throughout his realm and so everyone lived happily ever after … except for a couple of carpenters who had had their heads removed for failing to make a bed that came up to royal requirements).
The Imperial system
The British Empire, being predominantly a vehicle for trade, had a little more success at imposing its weights and measures upon the world … indeed, that is why the system of feet and inches; ounces and pounds; pints and gallons is called the Imperial system (of, or pertaining to, an empire). Even then, different towns often had differing ideas as to what constituted a pound and what qualified as short measure and, even today, there is a difference between the amount – and spelling – of units: a US gallon is 3.79 liters and a UK gallon, 4.55 litres.
The MKS system
Today, wherever possible, we use highly precise definitions based on constant phenomena that are observable by any scientist working anywhere in the world or, indeed, off it. A metre is now defined as the distance travelled by light in a vacuum in 1/299 792 458 of a second; a second is 9 192 631 770 cycles of radiation associated with the transition between the two hyperfine levels of the ground state of the caesium-133 atom (a statement that will be understandable by the end of Ch. 8). A kilogram, however, remains as the mass of a cylinder of French platinum-iridium until somebody can think of anything better.
The SI system
These additional units, which built upon the MKS system, were called the Système International D’unités, known as the SI system. Since its formal adoption in 1960, many more units have been added. There are now seven basic units (Table 1.1): in addition to the metre, the kilogram and the second, we now have the ampere, A, for electric current; for luminous intensity, the candela, cd; for temperature, kelvin, K; and for quantity of substance, the mole, mol.
Table 1.1 The seven base SI units
| Unit | Symbol | Definition |
|---|---|---|
| Metre | m | The distance travelled by light in a vacuum in 1/299 792 458 second |
| Kilogram | kg | Defined by the international prototype kilogram of platinum-iridium in the keeping of the International Bureau of Weights and Measures in Sèvres, France |
| Second | s | The duration of 9 192 631 770 periods of radiation associated with a specified transition of the cesium-133 atom |
| Ampere | A | The current that, if maintained in two wires placed one metre apart in a vacuum, would produce a force of 2 × 10−7 newton per metre of length |
| Kelvin | K | 1/273.16 of the triple point of pure water (corresponding to −273.15° on the Celsius scale and to −459.67° on the Fahrenheit scale). It is calculated by extrapolating the point at which an ideal gas and constant pressure would reach zero volume |
| Mole | mol | The amount of a given substance that contains as many elementary entities as there are atoms in 0.012 kilogram of carbon-12 |
| Candela | cd | The intensity in a given direction of a source emitting radiation of frequency 540 × 1012 hertz and that has a radiant intensity in that direction of 1/683 watt per steradian |
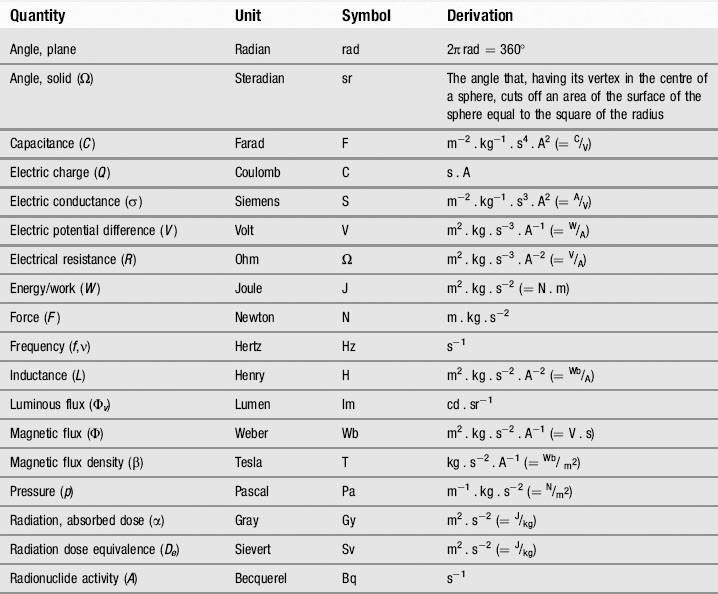
The three original derived units have also been built upon considerably; however, all these other SI units can – as Tables 1.2, 1.3 and 1.4 show – be defined in terms of these seven basic units, either directly or indirectly. Many of these units have their own special names (such as the newton and joule). At this stage, there may appear to be an alarming number of these units with peculiar names that define quantities of which you may never have heard – and the lists given are by no means complete, these are merely the units that a health professional is likely to encounter! However, by the time you have finished the book, all these terms should be like regular acquaintances. Do not try to memorize them all at this stage, rather familiarize yourself with the names and use the table as a reference so that, when you encounter a new term or an unfamiliar symbol, you can refer back and learn the detail in its correct context.
Table 1.2 Some derived SI units
| Quantity | Unit | Symbol |
|---|---|---|
| Acceleration (a) | Metres per second per second | m/s2 = ms−2 |
| Area (A) | Square metre | m2 |
| Current density (j) | Ampere per metre | A/m2 = Am−2 |
| Density (ρ) | Kilogram per cubic metre | kg/m3 = kgm−3 |
| Luminance (Lv) | Candela per square metre | cd/m2 = cdm−2 |
| Magnetic field strength (H) | Ampere per metre | A/m = Am−1 |
| Substance concentration (c) | Mole per cubic metre | mol/m3 = mol.m−3 |
| Volume (V) | Cubic metre | m3 |
| Velocity (v) | Metres per second | m/s = ms−1 |
| Wave number (σ) | Reciprocal metre | m−1 |
Table 1.4 Some SI units with derived unit names
| Quantity | Unit | Derivation |
|---|---|---|
| Absorbed dose rate | Gray per second | Gy.s−1 |
| Angular acceleration (α) | Radian per second per second | rad.s−2 |
| Angular velocity (ω) | Radian per second | rad.s−1 |
| Electric charge density (P) | Coulomb per cubic metre | C.m−3 |
| Electric field strength (E) | Volt per metre | V.m−1 |
| Exposure, X- & γ-ray | Coulomb per kilogram | C.kg−1 |
| Moment of force (Fm) | Newton metre | N.m |
| Thermal conductivity (λ) | Watts per metre per kelvin | Wm−1K−1 |
| Viscosity (π) | Pascal second | Pa.s |
There is one other trick to know about when it comes to units, which can – and often does – serve as an alternative to scientific nomenclature. In everyday conversation, it becomes a bit tedious to say ‘it’s six times ten to the three metres to the nearest town’ so, instead, we say ‘it’s six kilometres’, ‘kilo’ being a prefix meaning ‘one thousand’. Scientists do the same in their everyday conversation too: there are a stack of these prefixes, some of which – kilo (103), centi (10−2), milli (10−3) – you will be familiar with as you will with their common abbreviations: k, c and m respectively. Table 1.5 shows the abbreviations and symbols from 10−24 to 1024, which, whilst not exhaustive, is enough for most eventualities that you are likely to encounter. So you are now able to express large and small quantities in two ways, by saying, for example:
Table 1.5 Commonly used prefixes for SI units. Note the use of capital letters for units of 106 and above and lower case for 103 and below
| 1024 | Yotta | Y |
| 1021 | Zetta | Z |
| 1018 | Exa | E |
| 1015 | Peta | P |
| 1012 | Tera | T |
| 109 | Giga | G |
| 106 | Mega | M |
| 103 | Kilo | k |
| 102 | Hecto | h |
| 101 | Deka | da |
| 10−1 | Deci | d |
| 10−2 | Centi | c |
| 10−3 | Milli | m |
| 10−6 | Micro | μ |
| 10−9 | Nano | n |
| 10−12 | Pico | p |
| 10−15 | Femto | f |
| 10−18 | Atto | a |
| 10−21 | Zepto | z |
| 10−24 | Yocto | y |
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


 DICTIONARY DEFINITION
DICTIONARY DEFINITION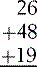
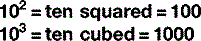
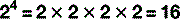
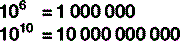
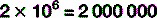
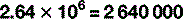
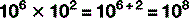
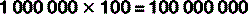
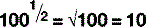
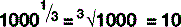
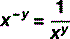
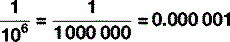
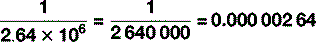
 Fact File
Fact File inch) and it was not until 1959 that a standard length was agreed.
inch) and it was not until 1959 that a standard length was agreed.