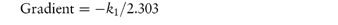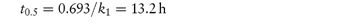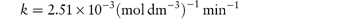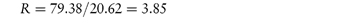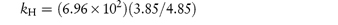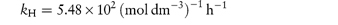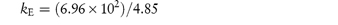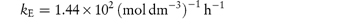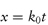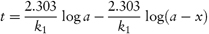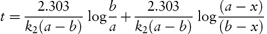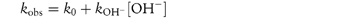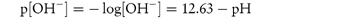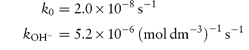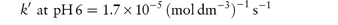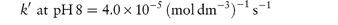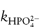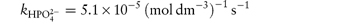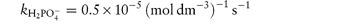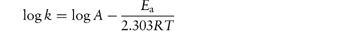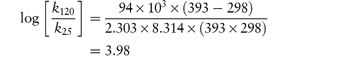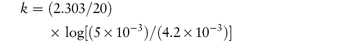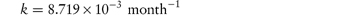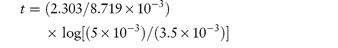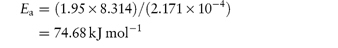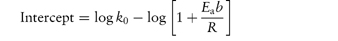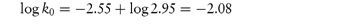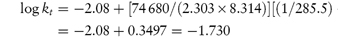Scheme 3.1 Examples of chemical groups susceptible to hydrolysis.

Drugs that contain ester linkages include acetylsalicylic acid, physostigmine, methyldopate, tetracaine and procaine. Ester hydrolysis is usually a bimolecular reaction involving acyl-oxygen cleavage. For example, the hydrolysis of procaine is shown in Scheme 3.2.

Scheme 3.2 Hydrolysis of the ester group of procaine.

The hydrolysis of amides involves the cleavage of the amide linkage as, for example, in the breakdown of the local anaesthetic cinchocaine (Scheme 3.3). This type of link is also found in drugs such as chloramphenicol, ergometrine and benzylpenicillin sodium.

Scheme 3.3 Hydrolysis of the amide linkage of cinchocaine.

As examples of lactam ring hydrolysis we can consider the decomposition of nitrazepam and chlordiazepoxide, which is discussed in more detail later (section 3.2.7). Other drugs, apart from the benzodiazepines, which are susceptible to lactam-ring hydrolysis include the penicillins and cephalosporins. The lactones pilocarpine and spironolactone are susceptible to hydrolysis, as are the imides glutethimide and ethosuximide.

A review by LePree and Connors¹ gives a detailed account of the mechanisms involved in the hydrolytic degradation of drugs.

Controlling drug hydrolysis in solution

Optimisation of formulation

Hydrolysis is frequently catalysed by hydrogen ions (specific acid catalysis) or hydroxyl ions (specific base catalysis) and also by other acidic or basic species that are commonly encountered as components of buffers. This latter type of catalysis is referred to as general acid–base catalysis. Both types of catalysis will be dealt with in greater depth in section 3.4.1. Several methods are available to stabilise a solution of a drug that is susceptible to acid–base-catalysed hydrolysis. The usual method is to determine the pH of maximum stability from kinetic experiments at a range of pH values and to formulate the product at this pH (section 3.4.1). Alteration of the dielectric constant by the addition of non-aqueous solvents such as alcohol, glycerin or propylene glycol may in many cases reduce hydrolysis (section 3.4.1).

Since only that portion of the drug which is in solution will be hydrolysed, it is possible to suppress degradation by making the drug less soluble. The stability of penicillin in procaine penicillin suspensions was significantly increased by reducing its solubility by using additives such as citrates, dextrose, sorbitol and gluconate. Adding a compound that forms a complex with the drug can increase stability. The addition of caffeine to aqueous solutions of benzocaine, procaine and tetracaine was shown to decrease the base-catalysed hydrolysis of these local anaesthetics in this way. In many cases, solubilisation of a drug by surfactants protects against hydrolysis, as discussed in section 3.4.1.

Modification of chemical structure of drug

The control of drug stability by modifying chemical structure using appropriate substituents has been suggested for drugs for which such a modification does not reduce therapeutic efficiency. The Hammett linear free-energy relationship for the effect of substituents on the rates of aromatic side-chain reactions, such as the hydrolysis of esters, is given by

where k and k₀ are the rate constants for the reaction of the substituted and unsubstituted compounds, respectively, σ is the Hammett substituent constant (which is determined by the nature of the substituents and is independent of the reaction) and ρ is the reaction constant, which is dependent on the reaction, the conditions of reaction and the nature of the side-chains undergoing reaction. Thus, a plot of log k against the Hammett constant (values are readily available in the literature²) is linear if this relationship is obeyed, with a slope of ρ. This concept has been used, for example, in the production of the best substituents for allylbarbituric acids to obtain optimum stability.³

3.1.2 Oxidation⁴

After hydrolysis, oxidation is the next most common pathway for drug breakdown. However, whereas the hydrolytic degradation of drugs has been thoroughly studied, their oxidative degradation has received comparatively little attention. Indeed, in cases where simultaneous hydrolytic and oxidative degradation can occur, the oxidative process has usually been eliminated by storage under anaerobic conditions without an investigation of the oxidative mechanism.

Oxidation processes

Oxidation involves the removal of an electropositive atom, radical or electron, or the addition of an electronegative atom or radical. Oxidative degradation can occur by autoxidation, in which a reaction is uncatalysed and proceeds quite slowly under the influence of molecular oxygen, or may involve chain processes consisting of three concurrent reactions – initiation, propagation and termination. Initiation can be via free radicals formed from organic compounds by the action of light, heat or transition metals such as copper and iron that are present in trace amounts in almost every buffer. The propagation stage of the reaction involves the combination of molecular oxygen with the free radical R^• to form a peroxy radical ROO^•, which then removes H from a molecule of the organic compound to form a hydroperoxide, ROOH, and in so doing creates a new free radical (Scheme 3.4).

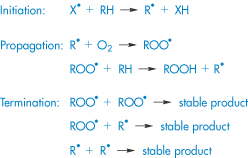
Scheme 3.4 Simplified oxidation scheme involving a chain process.

The reaction proceeds until the free radicals are destroyed by inhibitors or by side-reactions that eventually break the chain. The rancid odour that is a characteristic of oxidised fats and oils is due to aldehydes, ketones and short-chain fatty acids, which are the breakdown products of the hydroperoxides. Peroxides (ROOR′) and hydroperoxides (ROOH) are photolabile, breaking down to hydroxyl (HO^•) and/or alkoxyl (RO^•) radicals, which are themselves highly oxidising species. The presence of residual peroxides in polyoxyethylene glycols is a cause for concern when these excipients are used in formulation, as for example in the case of fenprostalene.⁵

Drugs susceptible to oxidation

We will consider some examples of drugs and excipients that are subject to oxidative degradation owing to the possession of functional groups that are particularly sensitive to oxidation.

Steroids and sterols represent an important class of drugs that are subject to oxidative degradation through the possession of carbon–carbon double bonds (alkene moieties) to which peroxyl radicals can readily add. Similarly, polyunsaturated fatty acids, commonly used in drug formulations, are particularly susceptible to oxidation and care must be exercised to minimise degradation in formulations containing high concentrations of, for example, vegetable oils.⁶ For drugs such as the cholesterol-lowering agent simvastatin (I) that contain conjugated double bonds, addition of peroxyl radicals may lead to the formation of polymeric peroxides (simvastatin polymerises up to a pentamer⁷), cleavage of which produces epoxides which may further degrade into aldehydes or ketones.

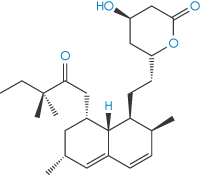
Structure I Simvastatin

Polyene antibiotics, such as amphotericin B (II), which contains seven conjugated double bonds (heptaene moiety), are subject to attack by peroxyl radicals, leading to aggregation and loss of activity.⁸

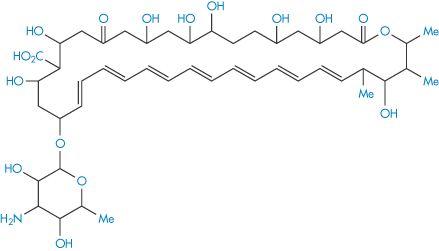
Structure II Amphotericin B

The oxidation of phenothiazines to the sulfoxide involves two single-electron transfer reactions involving a radical cation intermediate, as shown in Scheme 3.5. The sulfoxide is subsequently formed by reaction of the cation with water.

Scheme 3.5 Oxidation of phenothiazines.

The ether group in drugs such as econazole nitrate (III) and miconazole nitrate (IV) is susceptible to oxidation. The process involves removal of hydrogen from the C–H bonds in the α-position to the oxygen to produce a radical, which further degrades to α-hydroperoxides and eventually to aldehydes, ketones, alcohols and carboxylic acids.

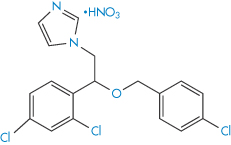
Structure III Econazole nitrate

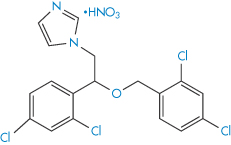
Structure IV Miconazole nitrate

Stabilisation against oxidation

Various precautions should be taken during manufacture and storage to minimise oxidation. The oxygen in pharmaceutical containers should be replaced with nitrogen or carbon dioxide; contact of the drug with heavy-metal ions such as iron, cobalt or nickel that catalyse oxidation should be avoided; and storage should be at reduced temperatures.

Antioxidants

It is very difficult to remove all of the oxygen from a container and even traces of oxygen are sufficient to initiate the oxidation chain. The propagation of the chain reaction may be prevented or delayed by adding low concentrations of compounds that act as inhibitors. Such compounds are called antioxidants and interrupt the propagation by interaction with the free radical. The antioxidant free radical so formed is not sufficiently reactive to maintain the chain reaction and is eventually annihilated. The structures of some commonly used antioxidants are given in Scheme 3.6. Reducing agents such as sodium metabisulfite may also be added to formulations to prevent oxidation. These compounds are more readily oxidised than the drug and so protect it from oxidation by consuming the oxygen. They are particularly effective in closed systems in which the oxygen cannot be replaced once it has been consumed. Chelating agents, such as ethylenediaminetetraacetic acid derivatives, may also protect the drug from autoxidation. These act by forming complexes with the heavy-metal ions that are often required to initiate oxidation reactions. Oxidation is catalysed by unprotonated amines such as aminophylline, and hence admixture of susceptible drugs with such compounds should be avoided.

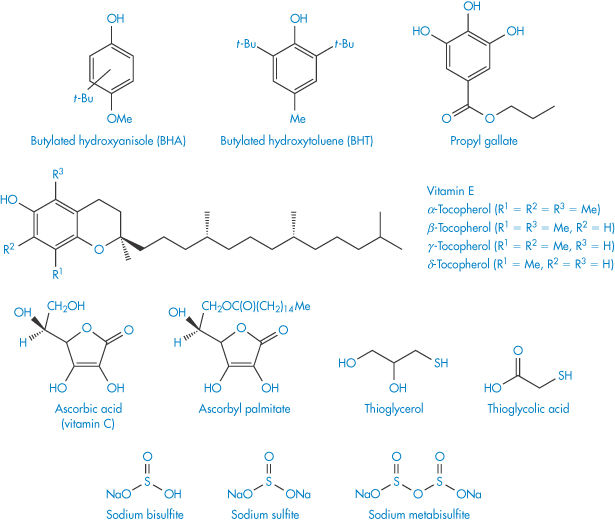
Scheme 3.6 Structures of some common antioxidants.

3.1.3 Isomerisation

Isomerisation is the process of conversion of a drug into its optical or geometric isomers. Since the various isomers of a drug are frequently of different activities, such a conversion may be regarded as a form of degradation, often resulting in a serious loss of therapeutic activity. For example, the appreciable loss of activity of solutions of adrenaline at low pH has been attributed to racemisation – the conversion of the therapeutically active form, in this case the levorotatory form, into its less-active isomer.

In acidic conditions the tetracyclines undergo epimerisation – a change of configuration at only one chiral centre. In this case, the change of configuration occurs at carbon atom 4 to form an equilibrium mixture of tetracycline and the epimer, 4-epi-tetracycline (Scheme 3.7). The 4-epi-tetracycline is toxic and its content in medicines is restricted to not more than 3%. The epimerisation follows the kinetics of a first-order reversible reaction (see equation 3.16). The degradation rate is pH-dependent (maximum epimerisation occurring at pH 3.2) and is also catalysed by phosphate and citrate ions.

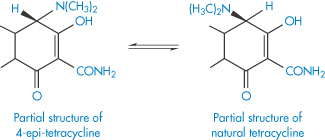
Scheme 3.7 Epimerisation of tetracyclines.

Although limits are set by pharmacopoeias on the level of the toxic 4-epi-anhydrotetracycline in tetracycline products, there may still be a problem when generic products are synthesised. As discussed in Chapter 16, even if the limit on these toxic impurities is very low (say, 0.005%), there may be three products (or the same product in different batches) with levels of such an impurity at 0.0048%, 0.004% and 0.002%.

Docetaxel is approved by the US Food and Drug Administration for treatment of locally advanced or metastatic breast cancer, head and neck cancer, gastric cancer, hormone-refractory prostate cancer and non-small-cell lung cancer. One of the principal paths of degradation of docetaxel is the epimerisation of the hydroxyl group at position 7, which results in the formation of 7-epidocetaxol (Scheme 3.8). The products of degradation have reduced activity or are completely inactive; these products demonstrate pharmacological and toxicological profiles which may be completely different from docetaxel.⁹

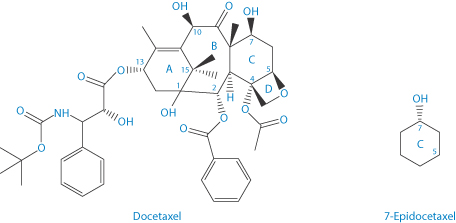
Scheme 3.8 Epimerisation of the hydroxyl group at position 7 of docetaxel to form 7-epidocetaxel.

Cephalosporin esters are widely used as intermediates in cephalosporin synthesis and as prodrugs for oral administration of parenteral cephalosporins. These esters undergo reversible base-catalysed isomerisation according to the mechanism shown in Scheme 3.9. A proton in the 2-position is abstracted by a base (B) and the resulting carbanion can be reprotonated in the 4-postion, giving a Δ²-ester. On hydrolysis, Δ²-cephalosporin esters yield Δ²-cephalosporins, which are biologically inactive.

Scheme 3.9 Proposed mechanism for the base-catalysed isomerisation of cephalosporin esters.

Reproduced from Richter WF et al. On the mechanism of isomerization of cephalosporin esters. J Pharm Sci 1990;79:185. Copyright Wiley-VCH Verlag GmbH & Co. KGaA. Reproduced with permission.

Cis-trans isomerisation may be a cause of loss of potency of a drug if the two geometric isomers have different therapeutic activities. Vitamin A (all-trans-retinol) is enzymatically oxidised to the aldehyde and then isomerised to yield 11-cis-retinal (Scheme 3.10), which has a decreased activity compared with the all-trans molecule.

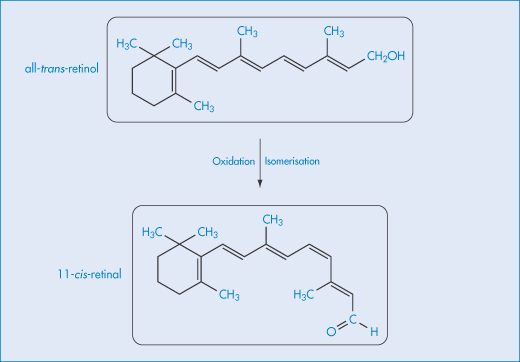
Scheme 3.10 Isomerisation of vitamin A.

3.1.4 Photochemical decomposition¹⁰

Many pharmaceutical compounds, including the phenothiazine tranquillisers, hydrocortisone, prednisolone, riboflavin, ascorbic acid and folic acid, degrade when exposed to light. As a result there will be a loss of potency of the drug, often accompanied by changes in the appearance of the product, such as discoloration or formation of a precipitate. Photodecomposition might occur not only during storage but also during usage of the product. For example, sunlight is able to penetrate the skin to a sufficient depth to cause photodegradation of drugs circulating in the surface capillaries or in the eyes of patients receiving the drug. Phototoxic dermatitis may occur when the allergen or irritant is activated by sunlight, as discussed in Chapter 12.

Primary photochemical reaction occurs when the wavelength of the incident light is within the wavelength range of absorption of the drug (usually within the ultraviolet range, unless the drug is coloured), so that the drug molecule itself absorbs radiation and degrades. Photodegradation may also occur with drugs that do not directly absorb the incident radiation, as a consequence of absorption of radiation by excipients in the formulation (photosensitisers) that transfer the absorbed energy to the drug, causing it to degrade. In assessing the photostability of a product it is therefore necessary to consider the final formulation rather than simply the drug itself. The rate of the photodegradation is dependent on the rate at which light is absorbed by the system and also the efficiency of the photochemical process. In formulations that contain low drug concentrations, the primary photochemical reaction follows first-order kinetics; the kinetics are more complicated at higher concentrations and in the solid state because most of the light is then absorbed near the surface of the product.

Although it is difficult to predict which drugs are likely to be prone to photodegradation, there are certain chemical functions that are expected to introduce photoreactivity, including carbonyl, nitroaromatic and N-oxide functions, aryl halides, alkenes, polyenes and sulfides.¹¹ The mechanisms of photodegradation are of such complexity as to have been fully elucidated in only a few cases. We will consider two examples – chlorpromazine and ketoprofen.

The phenothiazine chlorpromazine is rapidly decomposed under the action of ultraviolet light, the decomposition being accompanied by discoloration of the solutions (Scheme 3.11).

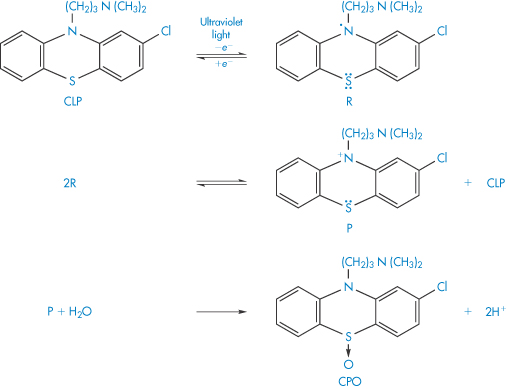
Scheme 3.11 Mechanism proposed for the effect of ultraviolet light on chlorpromazine (CLP). The first step of the photodegradation is the loss of an electron to yield the semiquinone free radical R. Further stages in the degradation yield the phenazathonium ion P, which is thought to react with water to yield chlorpromazine sulfoxide (CPO). The chlorpromazine sulfoxide is itself photolabile and further decomposition occurs. Other products of the photooxidation include chlorpromazine N-oxide and hydroxychlorpromazine.

Reproduced from Merkle FH, Discher CA. Electrochemical oxidation of chlorpromazine hydrochloride.  J Pharm Sci 1964;53:620. Copyright Wiley-VCH Verlag GmbH & Co. KGaA. Reproduced with permission.

Chlorpromazine behaves differently towards ultraviolet irradiation under anaerobic conditions. A polymerisation process has been proposed¹² that involves the liberation of HCl in its initial stages. The polymer (V) was isolated and upon intracutaneous injection produced a bluish-purple discoloration typical of that observed in some patients receiving prolonged chlorpromazine medication. It was suggested that the skin irritation that accompanies the discoloration may be a result of the HCl liberation during photodecomposition.

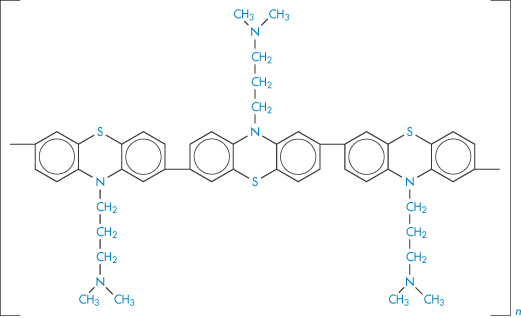
Structure V Polymer produced by the ultraviolet irradiation of chlorpromazine under anaerobic conditions.

The photodegradation of ketoprofen can involve decarboxylation to form an intermediate that then undergoes reduction, or dimerisation of the ketoprofen itself, as illustrated in Scheme 3.12.

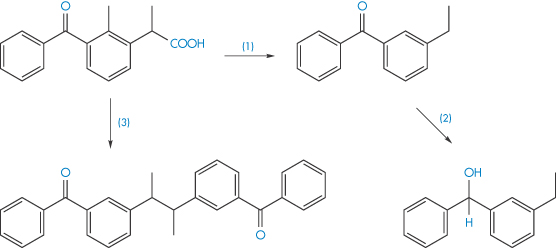
Scheme 3.12 Photodegradation of ketoprofen by decarboxylation (reaction 1) and subsequent reduction (reaction 2), and also by dimerisation of the ketoprofen (reaction 3).

Reproduced from Tønnesen HH. Int J Pharm 2001;225:1.

Stabilisation against photochemical decomposition

Pharmaceutical products can be adequately protected from photo-induced decomposition by the use of coloured-glass containers and storage in the dark. Amber glass excludes light of wavelength <470 nm and so affords considerable protection of compounds sensitive to ultraviolet light. Coating tablets with a polymer film containing ultraviolet absorbers has been suggested as an additional method for protection from light. In this respect, a film coating of vinyl acetate containing oxybenzone as an ultraviolet absorber has been shown¹³ to be effective in minimising the discoloration and photolytic degradation of sulfasomidine tablets.

3.1.5 Polymerisation

Polymerisation is the process by which two or more identical drug molecules combine together to form a complex molecule. It has been demonstrated that a polymerisation process occurs during the storage of concentrated aqueous solutions of aminopenicillins, such as ampicillin sodium. The reactive β-lactam bond of the ampicillin molecule is opened by reaction with the side-chain of a second ampicillin molecule and a dimer is formed (Scheme 3.13). The process can continue to form higher polymers. Such polymeric substances have been shown to be highly antigenic in animals and they are considered to play a part in eliciting penicilloyl-specific allergic reactions to ampicillin in humans. The dimerising tendency of the aminopenicillins increases with the increase in the basicity of the side-chain group, the order in terms of increasing rates being:
cyclacillin 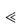ampicillin < epicillin < amoxicillin.

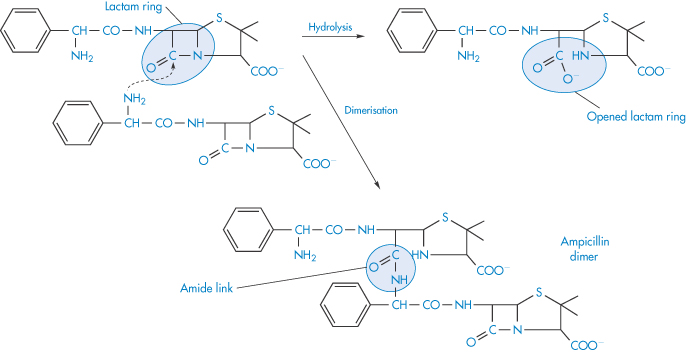
Scheme 3.13 Dimerisation and hydrolysis of ampicillin.

Reproduced with permission from Bundgaard H. Polymerization of penicillins: kinetics and mechanism of di- and polymerization of ampicillin in aqueous solution. Acta Pharm Suec 1976;13:9.

Impurities in amoxicillin samples can include the dimer, trimer and other oligomers which, as discussed in Chapter 12, are possibly prime culprits in penicillin allergies as they are formed with peptide bonds and resemble peptides.

The hydrate of formaldehyde, HOCH₂OH, may under certain conditions polymerise in aqueous solution to form paraformaldehyde, HOCH₂(OCH₂)_nOCH₂OH, which appears as a white deposit in the solution. The polymerisation may be prevented by adding to the solution 10–15% of methanol.

3.2 Kinetics of chemical decomposition in solution

Before we can predict the shelf-life of a dosage form it is essential to determine the kinetics of the breakdown of the drug under carefully controlled conditions. Unfortunately, drug decomposition often does not follow simple reaction schemes and in this section we will look not only at the traditional ways of classifying reactions but also at some of the complications that can arise with pharmaceutical preparations, which confuse this simple classification.

3.2.1 Classifying reactions: the order of reaction

Reactions are classified according to the number of reacting species whose concentration determines the rate at which the reaction occurs, i.e. the order of reaction. We will concentrate mainly on zero-order reactions, in which the breakdown rate is independent of the concentration of any of the reactants; first-order reaction, in which the reaction rate is determined by one concentration term; and second-order reactions, in which the rate is determined by the concentrations of two reacting species.

Experimentally we can monitor the rate of breakdown of the drug either by its decrease in concentration with time or alternatively by the rate of appearance of one of the breakdown products. If we represent the initial concentration of drug A as a mol dm⁻³ and if we find experimentally that x mol dm⁻³ of the drug has reacted in time t, then the amount of drug remaining at a time t is (a − x) mol dm⁻³ and the rate of reaction is

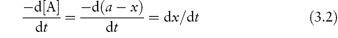
Notice that the term a is a constant and therefore disappears during differentiation. We will use dx/dt to describe the reaction rate in this section.

If we assume that a typical reaction between a drug molecule A and a reactant B occurs when two molecules are in collision, then we might expect that the number of collisions, and hence the reaction rate, would be proportional to the concentration of the two reacting molecules, i.e.

or

where the proportionality constant, k, is called the rate constant. The order of reaction is the sum of the exponents of the concentration terms in the rate equation and so this is an example of a second-order reaction. As we will see (section 3.4.1), many hydrolysis reactions are catalysed by H⁺, OH⁻ or buffer components and so we can write equation (3.3) as, for example,

k₂ is a second-order rate constant and has units of (concentration)⁻¹(time)⁻¹, for example (mol dm⁻³)⁻¹ min⁻¹. When the solution is buffered at constant pH, [H⁺] is now constant and we can write equation (3.4) as

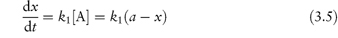
where k₁ = k₂[H⁺]. Since the rate of reaction now effectively depends on one concentration term it is a first-order reaction or, more correctly in this case, a pseudo first-order reaction (see section 3.2.3). The majority of decomposition reactions involving drugs fall into this category, either because the species reacting with the drug is maintained constant by buffering or because, as in the case of uncatalysed hydrolysis reactions, the water is in such large excess that any change in its concentration is negligible.

If as well as maintaining a constant amount of water in a reaction, we also maintain a fixed drug concentration, then equation (3.3) becomes

where k₀ = k₁[A] = k₂[A][B].

This type of reaction, which is called a zero-order reaction, can often occur in suspensions of poorly soluble drugs. In these systems the suspended drug slowly dissolves as the drug decomposes and so a constant drug concentration in solution is maintained.

We will now examine the ways in which we can determine the rate constants for these three types of reaction.

3.2.2 Zero-order reactions

In this type of reaction the decomposition proceeds at a constant rate and is independent of the concentrations of any of the reactants. The rate equation is given by equation (3.6) as

Integration of this equation (see Derivation Box 3A) gives

A plot of the amount remaining (as ordinate) against time (as abscissa) is linear with a slope of k₀ (concentration × time⁻¹).

Many decomposition reactions in the solid phase (section 3.3), or in suspensions, apparently follow zero-order kinetics. Figure 3.1 shows the hydrolysis of a suspension of acetylsalicylic acid.

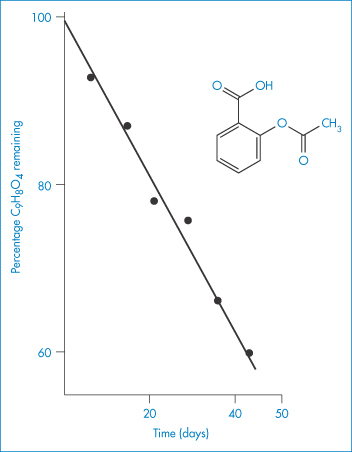
Figure 3.1 Hydrolysis of a suspension of acetylsalicylic acid at 34°C.

Reproduced from James KC. The hydrolysis of acetylsalicylic acid from aqueous suspension. J Pharm Pharmacol 1958;10:363. Copyright Wiley-VCH Verlag GmbH & Co. KGaA. Reproduced with permission.

3.2.3 First-order reactions

The rate of first-order reactions is determined by one concentration term and may be written using equation (3.5) as

Integration of this equation (see Derivation Box 3A) gives

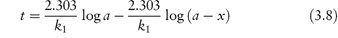
According to equation (3.8), a plot of the logarithm of the amount of drug remaining (as ordinate) as a function of time (as abscissa) is linear if the decomposition follows first-order kinetics. The first-order rate constant may be obtained from the gradient of the plot (gradient = −k₁/2.303). k₁ has the dimensions of time⁻¹.

The time taken for half of the reactant to decompose is referred to as the half-life of the reaction, t_0.5. The half-life of a first-order reaction may be calculated from equation (3.9) (Derivation Box 3A)

The half-life is therefore independent of the initial concentration of reactants. Example 3.1 shows the method of determination of rate constant and half-life for a drug which hydrolyses by first-order kinetics.

Even in the case of a reaction involving more than one reacting species, the rate may still follow first-order kinetics. The most common example of this occurs when one of the reactants is in such a large excess that any change in its concentration is negligible compared with changes in the concentration of the other reactants. This type of reaction is termed a pseudo first-order reaction. Such reactions are often met in stability studies of drugs that hydrolyse in solution, the water being in such excess that changes in its concentration are negligible and hence the rate of reaction is dependent solely on the drug concentration.

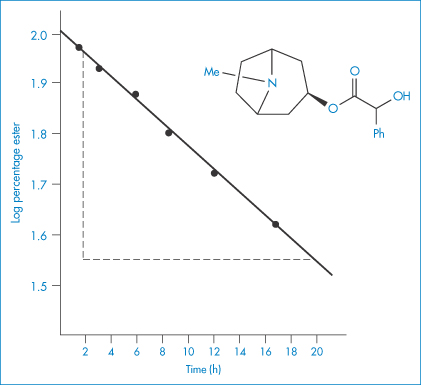
Figure 3.2 First-order plot for hydrolysis of homatropine in hydrochloric acid (0.226 mol dm⁻³) at 90°C.

Data from Krasowska MH et al. Stability of homatropine in aqueous solution. Dansk Tidsskr Farm 1968;42:170, with permission.

3.2.4 Second-order reactions

The rate of a second-order reaction is determined by the concentrations of two reacting species. The general rate equation is given by equation (3.3) as

In most second-order reactions the reactants have different initial concentrations, in which case the rate equation is given by

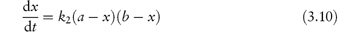
Integration of this equation, as shown in Derivation Box 3A, yields

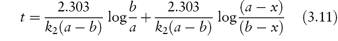
from which it is seen that k₂ can then be obtained from the gradient, 2.303/k₂(a − b), of a plot of t (as ordinate) against log[(a − x)/(b − x)] (as abscissa).

An examination of equation (3.11) shows that the second-order rate constant is dependent on the units used to express concentration; the units of k₂ are concentration⁻¹ time⁻¹.

For second-order reactions in which both concentration terms refer to the same reactant or in which the initial concentrations of the two reactants are the same we may write

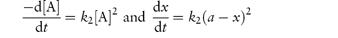
Integration as shown in Derivation Box 3A yields

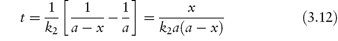
from which it is seen that a plot of t (ordinate) against x/[a(a − x)] (abscissa) yields a linear plot of gradient 1/k₂.

The half-life of a reaction that follows equation (3.12) is given by

Unlike t_0.5 for first-order reactions, the half-life of the second-order reaction is dependent on the initial concentration of reactants. It is not possible to derive a simple expression for the half-life of a second-order reaction with unequal initial concentrations.

3.2.5 Third-order reactions

Third-order reactions are only rarely encountered in drug stability studies involving, as they do, the simultaneous collision of three reactant molecules. The overall rate of ampicillin breakdown by simultaneous hydrolysis and polymerisation may be represented by an equation of the form

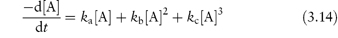
where k_a, k_b and k_c are the pH-dependent apparent rate constant for hydrolysis, uncatalysed polymerisation and the general acid–base-catalysed polymerisation of ampicillin, respectively.¹⁴ As seen from equation (3.14), the decomposition rate shows both second-order and third-order dependency on the total ampicillin concentration [A].

3.2.6 Determination of the order of reaction

The most obvious method of determining the order of a reaction is to determine the amount of drug decomposed after various intervals and to substitute the data into the integrated equations for zero-, first- and second-order reactions. The equation giving the most consistent value of k for a series of time intervals is that corresponding most closely to the order of the reaction. Alternatively, the data may be displayed graphically according to the linear equations for the various orders of reactions until a straight-line plot is obtained. Thus, for example, if the data yield a linear graph when plotted as t against log(a − x), the reaction is then taken to be first-order.

Fitting data to the standard rate equations may, however, produce misleading results if a fractional order of reaction applies. An alternative method of determining the order of reaction, which avoids this problem, is based on equation (3.15):

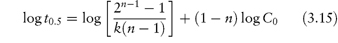
The half-life of the reaction is determined for a series of initial drug concentrations, C₀, and the order, n, is calculated from the slope of plots of log t_0.5 as a function of log C₀. The method of determination of order or reaction using equation (3.15) is shown by Example 3.2.

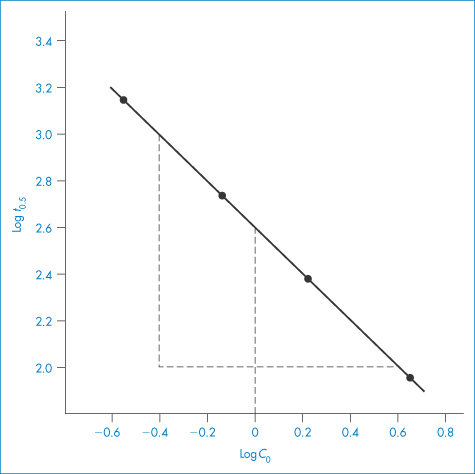
Figure 3.3 Plot of log of half-life (t_0.5) against log of initial drug concentration (C₀) (see Example 3.2).

3.2.7 Complex reactions

There are many examples of drugs in which decomposition occurs simultaneously by two or more pathways, or involves a sequence of decomposition steps or a reversible reaction. Indeed, the degradation pathways of some drugs include examples of each of these types of complex reactions. Modification of the rate equations is necessary whenever such reactions are encountered.

Reversible reactions

Treatment of the kinetics of a reversible reaction involves two rate constants: one, k_f, to describe the rate of the forward reaction, and the other, k_r, to describe the rate of the reverse reaction. For the simplest example in which both of these reactions are first-order, that is

the rate of decomposition of reactant is given by equation (3.16) (Derivation Box 3B):

If the initial concentration, [A]₀, the concentration at time t, [A] and the equilibrium concentration of reactant A, [A]_eq, are known, then, as explained in Derivation Box 3B, plots of t (as ordinate) against log[([A]₀ − [A]_eq)/([A] − [A]_eq)] should be linear with a gradient of 2.303/(k_f + k_r), from which values of the sum of the equilibrium constants k_f and k_r may be determined. Individual values of k_f  and  k_r can then be evaluated by combining this sum with the equilibrium constant K, which is the ratio of the concentration of products formed by each reaction at equilibrium,

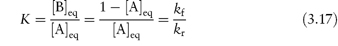
The epimerisation of tetracycline (see section 3.1.3) follows first-order reversible decomposition kinetics; Example 3.3 shows how to calculate rate constants for the epimerisation of this drug.

Parallel reactions

The decomposition of many drugs involves two or more pathways, the preferred route of reaction being dependent on reaction condition. Nitrazepam (VI) decomposes in two pseudo first-order parallel reactions, giving different breakdown products in solution and in the solid state, as illustrated in Scheme 3.14. Decomposition of nitrazepam tablets in the presence of moisture will occur by both routes, the ratio of the two products being dependent on the amount of water present.

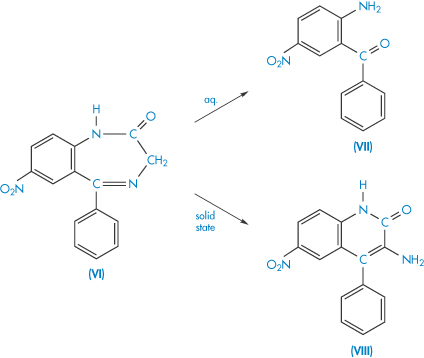
Scheme 3.14 Simplified decomposition scheme for nitrazepam (VI) in the solid state and aqueous solution. The main decomposition product is 2-amino-5-nitrobenzophenone (VII) in aqueous solution and 3-amino-6-nitro-4-phenyl-2(1H)-quinolone (VIII) in the solid state.

Reproduced with permission from Meyer W et al. Analysis and stability of various pharmaceutically interesting benzodiazepines. 1. Diazepam and nitrazepam, course of hydrolysis and determination of a circle contraction to isomeric quinolone derivatives. Pharmazie 1972;27:32.

In other cases decomposition may occur simultaneously by two different processes, as in the simultaneous hydrolysis and epimerisation of pilocarpine (Example 3.4).

The overall rate equation for a parallel reaction is the sum of the constants for each pathway. For example, for a decomposition of a drug X involving two pathways, each of which is first-order,

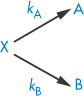
the rate equation is given by

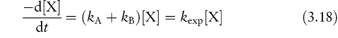
where k_A and k_B are the rate constants for the formation of A and B, respectively, and k_exp is the experimentally determined rate constant. Values of the rate constants k_A and k_B may be evaluated separately from plots of [A] or [B] against 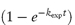which have gradients of k_A[X]₀/k_exp and k_B[X]₀/k_exp, respectively, as explained in Derivation Box 3B, or from the ratio R of the concentration of products formed by each reaction at equilibrium using

and

Consecutive reactions

The simplest example of a consecutive reaction is that described by a sequence

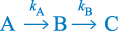
where each step is a non-reversible first-order reaction. The hydrolysis of chlordiazepoxide follows a first-order decomposition scheme similar to that described in this equation (Scheme 3.15).

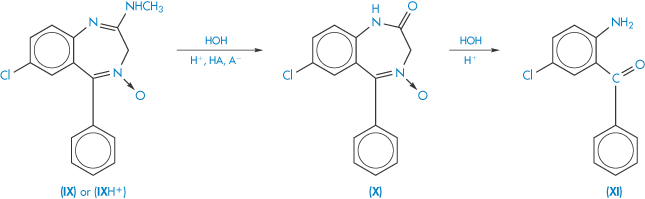
Scheme 3.15 Decomposition scheme for chlordiazepoxide. The neutral or cationic chlordiazepoxide (IX or IXH⁺) is transformed to the lactam (X) and, finally, in acidic solutions, to the yellow benzophenone (XI).

Reproduced from Maudling HV et al. Practical kinetics III: benzodiazepine hydrolysis. J Pharm Sci 1975;64:278. Copyright Wiley-VCH Verlag GmbH & Co. KGaA. Reproduced with permission.

The rate constants k_A and k_B and also the concentration of the breakdown product C may be estimated using equations given in Derivation Box 3B (equations 3B.16, 3B.18 and 3B.20).

3.3 Solid-dosage forms: kinetics of chemical decomposition

In spite of the importance of solid-dosage forms, there have been relatively few attempts to evaluate the detailed kinetics of decomposition. Most of the earlier work was carried out with the sole objective of predicting stability, and data were treated using the rate equations derived for reaction in solution. More recently, the mechanisms that were developed to describe the kinetics of decomposition of pure solids have been applied to pharmaceutical systems and some rationalisation of decomposition behaviour has been possible. A comprehensive account of this topic has been presented by Carstensen,^15,16 on which the following summary is based.

It is convenient to divide single-component systems into two categories – those solids that decompose to a solid product and a gas, and those that decompose to give a liquid and a gas.

3.3.1 Solids that decompose to give a solid and a gas

An example of this category is p-aminosalicylic acid, which decomposes to a solid (p-aminophenol) and a gas (carbon dioxide):

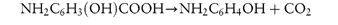
The decomposition curves that result from such a reaction show either (a) an initial rapid decomposition followed by a more gradual decomposition rate, or (b) an initial lag period, giving a sigmoidal appearance. The shape produced by (a) can usually be accounted for by topochemical (or contracting geometry) reactions and that produced in (b) by nucleation theories.

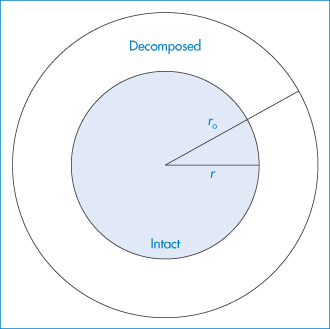
Figure 3.4 Model of sphere or cylinder used in theoretical treatment of topochemical reactions.

Reproduced from Carstensen JT. Stability of solids and solid dosage forms. J Pharm Sci 1974;63:1. Copyright Wiley-VCH Verlag GmbH & Co. KGaA. Reproduced with permission.

The model used in the treatment of topochemical decomposition is that of a cylinder or sphere (Fig. 3.4), in which it is assumed that the radius, r, of the intact chemical substance decreases linearly with time, t, i.e., r = r₀ − kt, where r₀ is the initial radius. For the contracting cylinder model, the mole fraction x decomposed at time t is given by

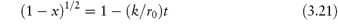
For the contracting sphere model,

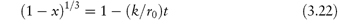
There are a few pharmaceutical examples of compounds that decompose by topochemical reaction. Thus, the decomposition of aspirin at elevated temperatures has been shown to conform to equation (3.21) (Fig. 3.5).

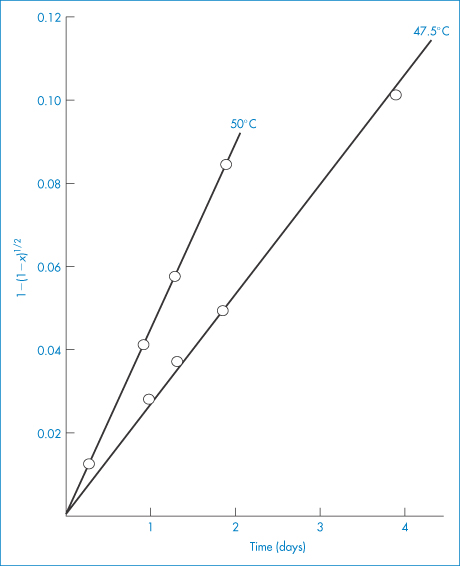
Figure 3.5 Decomposition of aspirin at elevated temperatures in tablets containing sodium bicarbonate, plotted according to equation (3.21).

Reproduced from Nelson E et al. Topochemical decomposition patterns of aspirin. J Pharm Sci 1974;63:755. Copyright Wiley-VCH Verlag GmbH & Co. KGaA. Reproduced with permission.

A similarity between equations (3.21) and (3.22) and the first-order rate equations was pointed out by Carstensen,¹⁵ who suggested that this similarity might account for the fact that many decompositions in solid-dosage forms appear to follow first-order kinetics.

The sigmoidal decomposition curves can be interpreted using the Prout and Tompkins model. This model assumes that the decomposition is governed by the formation and growth of active nuclei that occur on the surface as well as inside the crystals. The formation of product molecules sets up further strains in the crystal since the surface array of product molecules has a different unit cell from the original substance. The strains are relieved by the formation of cracks. Reaction takes place at the mouth of these cracks owing to lattice imperfections and spreads down into the crevices. Decomposition on these surfaces produces further cracking and so the chain reaction spreads.

The equation proposed to describe decomposition by this process is of the form

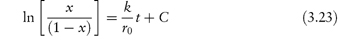
where C is a lag-time term.

The decomposition curves of p-aminosalicylic acid are sigmoidal (Fig. 3.6) and linear plots are produced when the data are plotted according to equation (3.23). Stability measurements made inadvertently in the lag periods of this type of decomposition would suggest zero-order kinetics.

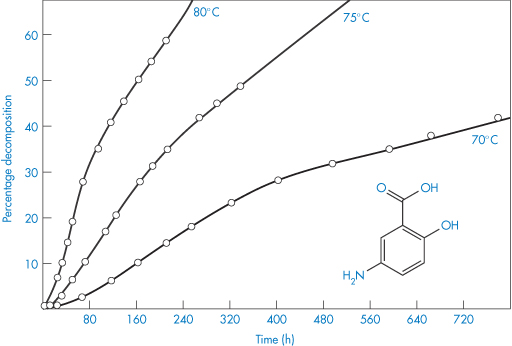
Figure 3.6 Degradation of powdered p-aminosalicylic acid in a dry atmosphere at elevated temperatures.

Reproduced from Kornblum SS, Sciarrone BJ. Decarboxylation of p-aminosalicylic acid in the solid state. J Pharm Sci 1964;53:935. Copyright Wiley-VCH Verlag GmbH & Co. KGaA. Reproduced with permission.

3.3.2 Solids that decompose to give a liquid and a gas

An example of a solid in this category is p-aminobenzoic acid, which decomposes into aniline and carbon dioxide. Decomposition causes a layer of liquid to form around the solid, which dissolves the solid. The decomposition curves show an initial lag period (Fig. 3.7) that corresponds to the establishment of the liquid layer. Beyond this region, the plot represents first-order decomposition of the solid in solution in its liquid decomposition products. There are thus two rate constants, that for the initial decomposition of the solid itself, and that for the decomposition of the solid in solution.

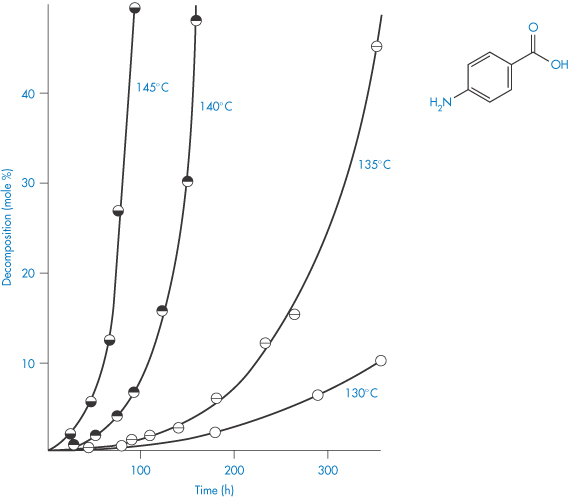
Figure 3.7 Decomposition curves of p-aminobenzoic acid at temperatures in the range 130–145°C showing the initial lag phase in p-aminobenzoic acid decomposition.

Reproduced from Carstensen JT, Musa MN. J Pharm Sci 1972;61:1113.

3.4 Factors influencing drug stability

Before we can suggest ways in which we might prevent the decomposition of drugs, we should first consider the various factors that accelerate the decomposition processes. For convenience we will consider liquid and solid-dosage forms separately, although, as we will see, there are similarities in the influence of several factors on drug breakdown in both.

3.4.1 Liquid-dosage forms

pH

pH is perhaps the most important parameter that affects the hydrolysis rate of drugs in liquid formulations; it is certainly the one that has been most widely examined.

Studying the influence of pH on degradation rate is not as simple as might at first be imagined. If the hydrolysis rate of the drug in a series of solutions buffered to the required pH is measured and the hydrolytic rate constant is then plotted as a function of pH, a pH–rate profile will be produced, but this will almost certainly be influenced by the buffers used to prepare the solutions. It is probable that a different pH–rate profile would be obtained using a different buffer. To understand why this should be, we have to consider not only the catalytic effect of hydrogen and hydroxyl ions, which is called specific acid–base catalysis, but also the possible accelerating effect of the components of the buffer system, which we refer to as general acid–base catalysis. These two types of acid–base catalysis can be combined together in a general expression as follows:

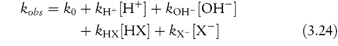
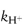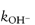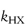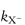In this equation, k_obs is the experimentally determined hydrolytic rate constant, k₀ is the uncatalysed or solvent catalysed rate constant, and are the specific acid and base catalysis rate constants respectively, and are the general acid and base catalysis rate constants, respectively, and [HX] and [X⁻] denote the concentrations of protonated and unprotonated forms of the buffer.

For a complete evaluation of the stability of the drug we need to evaluate the catalytic coefficients for specific acid and base catalysis and also to determine the catalytic coefficients of possible buffers that we might wish to use in the formulation.

First we will examine how to achieve a buffer-independent pH–rate profile, since this will show us at which pH the stability is greatest. By way of illustration we can consider a specific example of a stability study that has been reported for the antihypertensive vasodilator ciclosidomine. Experiments carried out at constant temperature and constant ionic strength using a series of different buffers over the pH range 3–6 produced the graphs shown in Fig. 3.8. These plots show that an increase of buffer concentration, particularly at pH 3, had a marked effect on the hydrolysis rate. The effect of the phosphate buffer on this system became less pronounced with increase of pH and was found to have a negligible effect above pH 7.5.

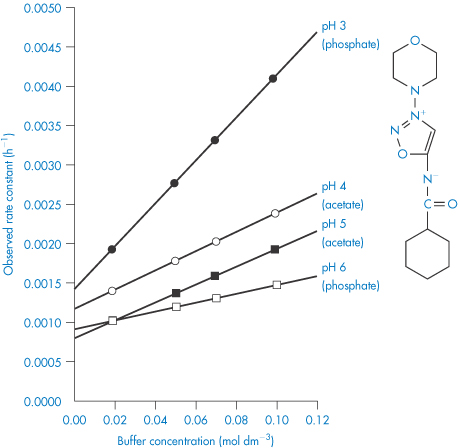
Figure 3.8 Effect of buffer concentration on the hydrolytic rate constant for ciclosidomine at 60°C as a function of pH.

Reproduced from Carney CF. Solution stability of ciclosidomine. J Pharm Sci 1987;76:393. Copyright Wiley-VCH Verlag GmbH & Co. KGaA. Reproduced with permission.

To remove the influence of the buffer, the reaction rate should be measured at a series of buffer concentrations at each pH and the data extrapolated back to zero concentration, as shown in Fig. 3.8. If these extrapolated rate constants are plotted as a function of pH, the required buffer-independent pH–rate profile will be obtained. Figure 3.9 illustrates the simple type of pH–rate profile that is obtained with codeine sulfate.

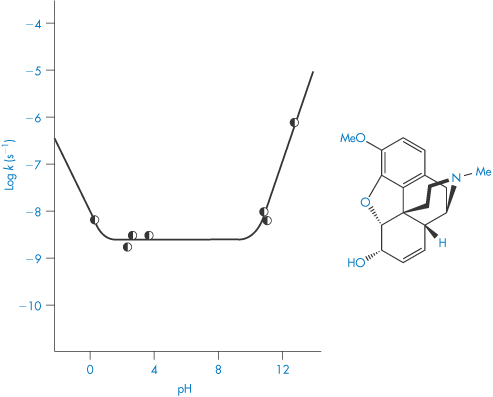
Figure 3.9 Log rate–pH profile for the degradation of codeine sulfate in buffer-free solutions at 60°C.

Reproduced from Powell MF. Enhanced stability of codeine sulfate: effect of pH, buffer, and temperature on the degradation of codeine in aqueous solution.  J Pharm Sci 1986;75:901. Copyright Wiley-VCH Verlag GmbH & Co. KGaA. Reproduced with permission.

As we can see from Fig. 3.9, this drug is very stable in unbuffered solution over a wide pH range but degrades relatively rapidly in the presence of strong acids or bases. Since the influence of buffer components has been removed, this plot allows us to calculate the rate constants for specific acid and base catalysis. Removing the terms for the effect of buffer from equation (3.24) we have

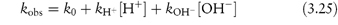
and consequently a plot of measured rate constant k_obs against the hydrogen ion concentration [H⁺] at low pH will have a gradient equal to the rate constant for acid catalysis. Similarly, of course, if we plot k_obs against [OH⁻] at high pH, the gradient will be the rate constant for base-catalysed hydrolysis. Example 3.5 illustrates the calculation of these catalytic coefficients.

The degradation of codeine is particularly susceptible to the effects of buffers. Its hydrolysis rate in 0.05 mol dm⁻³ phosphate buffer at pH 7 is almost 20 times faster than in unbuffered solution at this pH, so this is a good drug to use as an example of the determination of the influence of buffer components on the breakdown rate.

In phosphate buffers of neutral pH, the major buffer species are H₂PO₄⁻ and HPO₄²⁻, either of which may act as a catalyst for codeine degradation. To find out which of these is the stronger catalyst, we can treat the experimental data in the following way. In neutral pH solutions we can write the following expression for the observed rate constant,

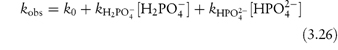
or

where 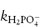and are the rate constants for catalysis by H₂PO₄⁻ and HPO₄²⁻ ions, respectively, and B_T is the total concentration of phosphate buffer. Notice that the terms for specific acid and base catalysis have little effect at this pH and we need not consider them in this treatment.

From equation (3.27), a plot of k_obs against B_T will have an intercept k₀ and a gradient k′. To find values for the catalytic coefficients, we rearrange the equation into the following linear form:

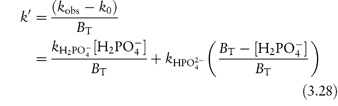
We can now see that a second plot of the apparent rate constant k′ against the fraction of the acid buffer component present, i.e. [H₂PO₄⁻/B_T], will have an intercept at [H₂PO₄⁻/B_T] = 0 equal to 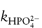. Furthermore, the k′ value at [H₂PO₄⁻/B_T] = 1 is the other catalytic coefficient, .

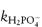The relationship between the ability of a buffer component to catalyse hydrolysis, denoted by the catalytic coefficient, k, and its dissociation constant, K, may be expressed by the Brønsted catalysis law as

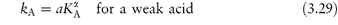
and

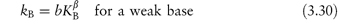
where a, b, α and β are constants characteristic of the solvent and temperature. α and β are positive and vary between 0 and 1.

In our treatment of the degradation of codeine sulfate we have not yet considered any effect that changes in its ionisation might have on its stability. Codeine has a pK_a of 8.2 at 25°C and so its ionisation state will change over the pH range 6–10. With this particular drug, the stability was not affected by any such changes. This is not the case with many drugs, however, and complex pH–rate profiles are often produced because of the differing susceptibility of the un-ionised and ionised forms of the drug molecule to hydrolysis.

By way of illustration we will look at the case of the hydrolysis of mecillinam (XII), which is an antimicrobially active amidopenicillamic acid. This amphoteric drug can exist as a cation, which we can write as MH₂⁺, a zwitterion MH^± or an anion M⁻. Figure 3.10 shows the pH–rate profile at zero buffer concentration. The reason this plot is so much more complex than that of codeine sulfate is that each of the species present in solution can undergo specific to varying extents and so each contributes to the overall profile shown in Fig. 3.10.

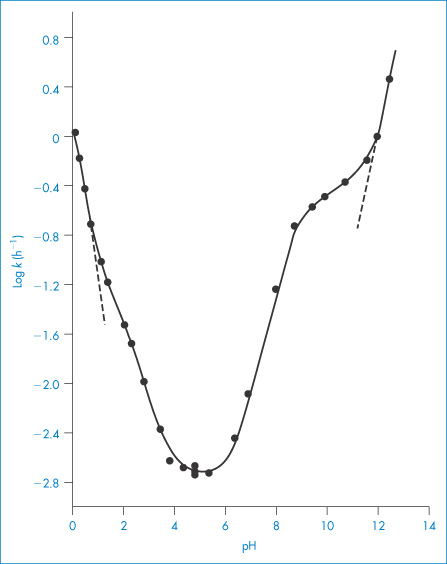
Figure 3.10 Log k–pH profile for the degradation of mecillinam in aqueous solution at 35°C (ionic strength = 0.5), where k is the apparent first-order rate constant for degradation in buffer-free solutions or in buffers showing no effect on rate of degradation.

Reproduced from Larsen C, Bundgaard H. Arch Pharm Chem 1977;5:66.

Structure XII Mecillinam

The various reactions thought to occur are

The part of the pH–rate profile at very low pH (below pH 1.5) is given entirely by reaction (1). This is because the mecillinam exists as the cation MH₂⁺, the hydrolysis of which will be acid-catalysed over this pH range. The shoulder in the pH–rate profile at around pH 2 coincides approximately with the first pK_a value of mecillinam and indicates an increased acid catalysis of the zwitterion relative to the cationic species. The decrease of hydrolysis rate constant with increasing pH up to pH 4 can be explained by assuming that both reactions (1) and (2) are occurring. We can see from Fig. 3.10 that the hydrolysis rate is almost constant between pH 4 and 6, and this suggests that the hydrolysis is water-catalysed (reaction 3) over this pH region. The hydrolysis rate now starts to increase with increasing pH, which indicates that base catalysis is now the dominating factor. Between pH 6.5 and the pK_a for ionisation of the amidino side-chains (pK_a2 = 8.79), it is reaction (4) that describes the hydrolysis rate. The plot changes slope at around pH 8 because it is affected by the changes that are occurring in the state of ionisation of the amidino side-chain. Above pH 12, the mecillinam exists in solution as the anion and this final part of the graph is described entirely by the base catalysis of this species (reaction 5).

Even though we may not always be able to explain the pH–rate profile as completely as we can for mecillinam, we can still, of course, choose the pH at which to buffer the drug solution for maximum stability. In the case of mecillinam this would be between pH 4 and 6.

We should also note that the oxidative degradation of some drugs in solution may be pH-dependent; for example, the oxidation of prednisolone is base-catalysed. Similarly, the oxidation of morphine occurs more rapidly in alkaline or neutral solution than in acid solution. The reason for this may be the effect of pH on the oxidation–reduction potential, E₀, of the drug.

The photodegradation of several drugs is also pH-dependent. For example, the photochemical decomposition of the benzodiazepine derivative midazolam (XIII) increases with pH,¹⁷ and ciprofloxacin (XIV) is most sensitive to photodegradation at slightly basic pH at which the drug is in zwitterionic form, the stability increasing when the pH is lowered to 3–4¹⁸ (Fig. 3.11).

During use, parenteral solutions may be exposed to light due to the low drug concentration and a large surface to volume ratio. Protection of infusion sets by a coloured or non-transparent outer package (e.g. foil) should always be considered, especially in the case of long-term infusion regimes.

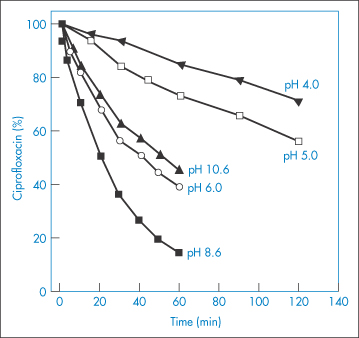
Figure 3.11 The effect of pH on the photodegradation of ciprofloxacin. Radiation source: mercury lamp at wavelength 313 nm.

Reproduced from Torniainen K et al. Int J Pharm 1996;132:53.

Structure XIII Midazolam

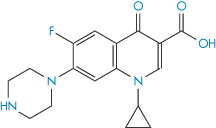
Structure XIV Ciprofloxacin

Temperature

Increase in temperature usually causes a very pronounced increase in the hydrolysis rate of drugs in solution, a fact which is used to good effect in the experimental studies of drug stability described above. Such studies are usually carried out at high temperatures, say 60°C or 80°C, because the hydrolysis rate is greater at these temperatures and can therefore be measured more easily. Of course, if a formulation has to be heat sterilised then its stability will, in any case, have to be measured at elevated temperatures. Figure 3.12 shows the pH–rate profiles for the degradation of codeine sulfate at several temperatures and also the calculated values at 25°C. We will now see how these calculated values can be obtained.

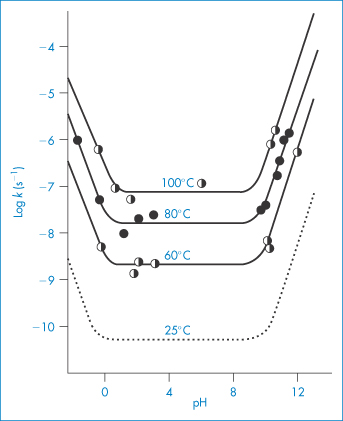
Figure 3.12 Log rate–pH profiles for the degradation of codeine sulfate in buffer-free solutions at several temperatures. The dashed line is the log rate–pH profile calculated from the Arrhenius equation.

Reproduced from Powell MF. Enhanced stability of codeine sulfate: effect of pH, buffer, and temperature on the degradation of codeine in aqueous solution.  J Pharm Sci 1986;75:901. Copyright Wiley-VCH Verlag GmbH & Co. KGaA. Reproduced with permission.

The equation that describes the effect of temperature on decomposition, and which shows us how to calculate the rate of breakdown at room temperature from measurements at much higher temperatures, is the Arrhenius equation.

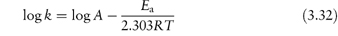
In this equation, E_a is the activation energy, which is the energy barrier that has to be overcome if reaction is to occur when two reactant molecules collide. A is the frequency factor and this is assumed to be independent of temperature for a given reaction. R is the gas constant (8.314 J mol⁻¹ K⁻¹) and T is the temperature in kelvins. We can see from equation (3.32) that a plot of the log rate constant, k, against the reciprocal of the temperature should be linear with a gradient of −E_a/2.303R. Therefore, assuming that there is not a change in the form of the reaction as the temperature is changed, we can extrapolate plots of log k against 1/T to any required temperature and so determine the rate of breakdown at that temperature. We can also, of course, calculate the activation energy from the gradient of this plot. Figure 3.13 shows Arrhenius plots for the breakdown of the drug ciclosidomine at several pH values.

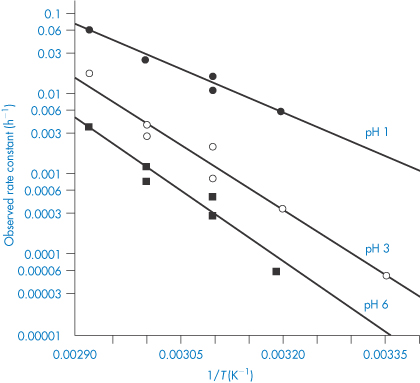
Figure 3.13 Arrhenius plots for the hydrolysis of ciclosidomine in buffer solutions at several pH values.

Reproduced from Carney CF. Solution stability of ciclosidomine. J Pharm Sci 1987;76:393. Copyright Wiley-VCH Verlag GmbH & Co. KGaA. Reproduced with permission.

When it is clear from stability determinations that a drug is particularly unstable at room temperature, then of course it will need to be labelled with instructions to store in a cool place. This is the case, for example, with injections of penicillin, insulin, oxytocin and vasopressin.

Ionic strength

We often need to add electrolytes to drug solutions, for example to control their tonicity. Consequently we must pay particular attention to any effect they may have on stability. In fact, the stability experiments that we considered earlier in this section should all be carried out at constant electrolyte concentration to avoid any confusion arising from possible differences in electrolyte effects between different systems.

The equation that describes the influence of electrolyte on the rate constant is the Brønsted–Bjerrum equation,

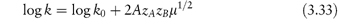
In this equation, z_A and z_B are the charge numbers of the two interacting ions and A is a constant for a given solvent and temperature (A = 0.509 in water at 298K). μ is the ionic strength of the solution, which we can calculate from

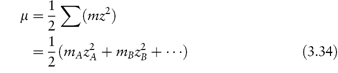
For example, if we have a monovalent drug ion of concentration 0.01 mol kg⁻¹ in the presence of 0.001 mol kg⁻¹ of Ca²⁺ ions then the ionic strength of the solution will be

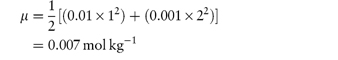
If the drug ion and the electrolyte ion are both monovalent, then the ionic strength will be equal to the total molality of the solution.

We can see from equation (3.33) that if we determine the rate constant of a reaction in the presence of a series of different concentrations of the same electrolyte and plot log k against μ^1/2, then the plot should be linear with an intercept of log k₀ and a gradient of 2Az_Az_B. This is frequently found to be the case even in solutions of high ionic strength, although equation (3.33) is strictly valid only for ionic strengths of less than 0.01 mol kg⁻¹. At higher ionic strengths (up to about 0.1 mol kg⁻¹) it is preferable to use the following modified form of the Brønsted–Bjerrum equation in which we plot log k against μ^1/2/(1 + μ^1/2).

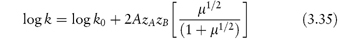
Figure 3.14 shows the degradation of phentolamine hydrochloride at two different pH values plotted according to equation (3.35). The gradients of these plots should be proportional to the product of the charge carried by the reactive species. Whether or not the gradient is positive or negative depends on the reaction involved. Reactions between ions of similar charge, for example, the acid-catalysed hydrolysis of a cationic drug ion, will produce plots of positive slope (i.e. the reaction rate will be increased by electrolyte addition), whereas the base-catalysed hydrolysis of positively charged drug species will produce negative gradients. Investigations of the influence of ionic strength on reaction rate may therefore be used to provide confirmation of the type of reaction that is occurring. For example, the gradients of the two plots of Fig. 3.14 are 0.260 and −1.759 at pH 3.1 and 7.2, respectively. Since the value of 2A at 90°C is 1.174, we can calculate values of the product z_Az_B of 0.221 and −1.498 at pH 3.1 and 7.2, respectively. These values are not integers as they should be if the reactions involved were simple acid- and base-catalysed reactions. This has been explained by suggesting complex reactions between the buffer species and the phentolamine at each pH.

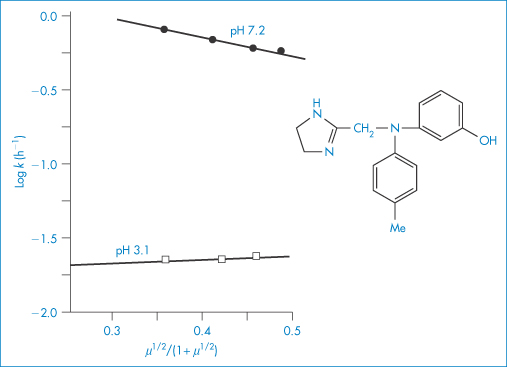
Figure 3.14 The effect of ionic strength, μ, on the hydrolytic rate constant, k, for phentolamine hydrochloride in buffer solutions of pH 3.1 and 7.2 at 90°C.

Solvent effects

Since we are considering the hydrolysis of drugs it might seem that an obvious way to reduce the breakdown would be to replace some or all of the water in the system with a solvent such as alcohol or propylene glycol. As we will see in this section, however, this is effective only in certain systems and in others it can, in fact, increase the rate of breakdown. The equation that allows us to predict the effect of the solvent on the hydrolysis rate is

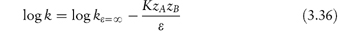
In this equation, K is a constant for a given system at a given temperature. We can see that a plot of log k as a function of the reciprocal of the dielectric constant, ε, of the solvent should be linear with a gradient of −Kz_Az_B and an intercept equal to the logarithm of the rate constant in a theoretical solvent of infinite dielectric constant. If the charges on the drug ion and the interacting species are the same, then we can see that the gradient of the line will be negative. In this case, if we replace the water with a solvent of lower dielectric constant then we will achieve the desired effect of reducing the reaction rate. If the drug ion and the interacting ion are of opposite signs, however, then the slope will be positive and the choice of a non-polar solvent will only result in an increase of decomposition.

Oxygen

Since molecular oxygen is involved in many oxidation schemes, we could use oxygen as a challenge to find out whether a particular drug is likely to be affected by oxidative breakdown. We would do this by storing solutions of the drug in ampoules purged with oxygen and then comparing their rate of breakdown with similar solutions stored under nitrogen. Formulations that are shown to be susceptible to oxidation can be stabilised by replacing the oxygen in the storage containers with nitrogen or carbon dioxide, by avoiding contact with heavy-metal ions and by adding antioxidants (see section 3.1.2).

Light

Photolabile drugs are usually stored in containers that exclude ultraviolet light, since exposure to light in this wavelength range is the most usual cause of photodegradation (see section 3.1.4). Amber glass is particularly effective in this respect because it excludes light of wavelength of less than about 470 nm. As an added precaution, it is always advisable to store photolabile drugs in the dark.

Surfactants

As might be expected, the presence of surfactants in micellar form has a modifying effect on the rate of hydrolysis of drugs. The magnitude of the effect depends on the difference in the rate constant when the drug is in aqueous solution and when it is solubilised within the micelle, and also on the extent of solubilisation. Thus

where k_obs, k_m and k_w are the observed, micellar and aqueous rate constants, respectively, and f_m and f_w are the fractions of drug associated with the micelles and aqueous phase, respectively. The value of k_m is dependent on the location of the drug within the micelle. A solubilisate may be incorporated into the micelle in a variety of locations. Non-polar compounds are thought to be solubilised within the lipophilic core and, as such, are likely to be more effectively removed from the attacking species than those compounds that are located close to the micellar surface. Where the drug is located near to the micellar surface, and therefore still susceptible to attack, the ionic nature of the surfactant is an important influence on decomposition rate. For base-catalysed hydrolysis, solubilisation into anionic micelles affords an effective stabilisation due to repulsion of OH⁻ by the micelles. Conversely, solubilisation into cationic micelles might be expected to cause an enhanced base-catalysed hydrolysis.

Many drugs associate to form micelles in aqueous solution (see section 5.3 in Chapter 5) and several studies have been reported of the effect of this self-association on stability. In micellar solutions of benzylpenicillin (500 000 units cm⁻³) the apparent rate of the hydrogen ion-catalysed degradation was increased twofold, but that of water and hydroxide ion-catalysed hydrolysis was decreased two- to threefold.¹⁹ Consequently, the pH profile was shifted to higher pH values and the pH of minimum degradation was found to be 7.0, compared with 6.5 for monomeric solution (8000 units cm⁻³). When compared at the respective pH–rate profile minima, micellar benzylpenicillin was reported to be 2.5 times more stable as the monomeric solutions under conditions of constant pH and ionic strength.

3.4.2 Semisolid-dosage forms

The chemical stability of active ingredients incorporated into ointments or creams is frequently dependent on the nature of the ointment or cream base used in the formulation. Hydrocortisone in a series of commercially available bases exhibits maximum decomposition in polyethylene glycol base.^20,21 The reported shelf-life was only 6 months in this base, which makes manufacture on a commercial basis an unreasonable proposition, considering the length of time involved in distribution of the drug from wholesaler to patient.

Not only should possible stability problems be borne in mind in the choice of ointment base at the formulation stage, but also similar care should be exercised if the ointment is diluted at a later stage. Such dilution is, unfortunately, common practice in cases where the practitioner wishes to reduce the potency of highly active topical preparations, particularly steroids. The pharmaceutical and biopharmaceutical dangers of this procedure have been stressed.²² Of particular interest here are the problems of drug stability, which can occur through the use of unsuitable diluents. An example has been cited of the dilution of betamethasone valerate cream with a cream base having a neutral to alkaline pH. Under such conditions, conversion of the 17-ester to the less-active betamethasone 21-ester can occur. Similarly, diluents containing oxidising agents could cause chemical degradation of fluocinolone acetate to less-active compounds.

Incorporation of drugs into gel structures frequently leads to a change in their stability, such as increased degradation of benzylpenicillin sodium in hydrogels of various natural and semisynthetic polymers.²³ At pH 6 in Carbopol hydrogels, the percentage of undecomposed pilocarpine at equilibrium is a simple function of the apparent viscosity of the medium.²⁴ The rate constant for degradation was not, however, significantly affected by changes in viscosity. Little influence of viscosity on the rate of oxidation of ascorbic acid in gels of polysorbate 80 has been noted.²⁵

3.4.3 Solid-dosage forms

Moisture

Water-soluble drugs present in a solid-dosage form will dissolve in any moisture that has adsorbed on the solid surface. The drug will now be in an aqueous environment and its decomposition could be influenced by many of the factors we have already discussed when dealing with liquid-dosage forms. For example, decomposition could now occur by hydrolytic cleavage of ester or amide linkages in the drug molecule and hence will be affected by the pH of the adsorbed moisture film. It is not surprising, therefore, that moisture is considered to be one of the most important factors that must be controlled in order to minimise decomposition.

We can get an idea of the extent to which moisture adsorption affects stability from the results shown in Fig. 3.15. We can see from this figure that an increase in the water vapour pressure (and therefore an increase in the amount of moisture associated with the drug) greatly increases the percentage decomposition at any given time. The problem is even more pronounced with drugs that are hygroscopic or that decompose to give hygroscopic products. In such cases it is worth trying to prepare a less hygroscopic salt of the drug.

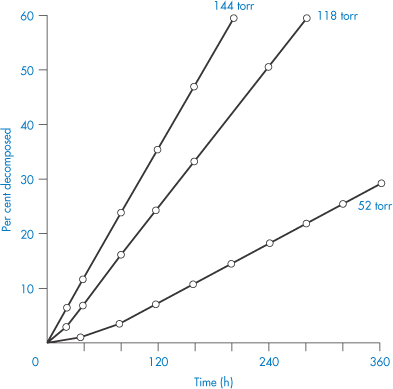
Figure 3.15 The effect of water vapour pressure on the decomposition of aminosalicylic acid.

Reproduced from Kornblum SS, Sciarrone BJ. Decarboxylation of p-aminosalicylic acid in the solid state. J Pharm Sci 1964;53:935. Copyright Wiley-VCH Verlag GmbH & Co. KGaA. Reproduced with permission.

In all cases it is important to minimise access of moisture during manufacture and storage. The correct selection of packaging is obviously important, although this is not as straightforward as you might at first think. For example, tablets containing a water-labile drug were found to be more stable in a water-permeable blister package at 50°C than in a sealed glass bottle and yet the situation was reversed at room temperature and 70% relative humidity.²⁶ The reason for this behaviour was attributed to the loss of considerable amounts of water through the film at 50°C, so improving stability, and the reverse diffusion at room temperature, so decreasing stability.

Excipients

One of the main ways in which the excipients of the solid-dosage form can affect the degradation of drugs is by increasing the moisture content of the preparation. Excipients such as starch and povidone have particularly high water contents (povidone contains about 28% equilibrium moisture at 75% relative humidity). However, whether this high moisture level has an effect on stability depends on how strongly it is bound and whether the moisture can come into contact with the drug. Magnesium trisilicate causes increased hydrolysis of aspirin in tablet form because, it is thought, of its high water content.

Many examples of the effects of tablet excipients on drug decompositions are reported in the pharmaceutical literature. Chemical interaction between components in solid-dosage forms may lead to increased decomposition. Replacement of the phenacetin in compound codeine and APC tablets by paracetamol in NHS formulations in Australia in the 1960s (because of the undesirable side-effects of phenacetin) led to an unexpected decreased stability of the tablets. The cause was later attributed to a transacetylation reaction between aspirin and paracetamol and also a possible direct hydrolysis of the paracetamol (Scheme 3.16).

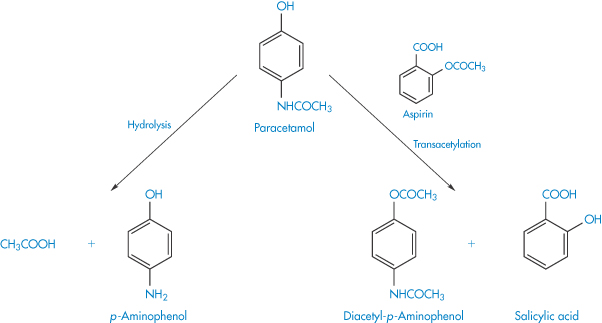
Scheme 3.16 Reactions showing the postulated transacetylation between aspirin and paracetamol and the direct hydrolysis of paracetamol.

Reproduced from Boggianno BG et al. Aust J Pharm 1970;51:S14.

Figure 3.16 shows the increased generation of free salicylic acid at 37°C in the tablets containing paracetamol. It is interesting to note from this figure the effect on stability of tablet excipients. Addition of 1% talc caused only a minimal increase in the decomposition, while 0.5% magnesium stearate increased the breakdown rate dramatically.

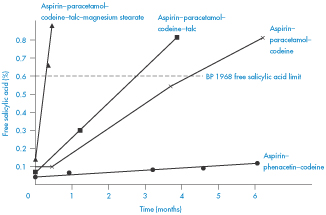
Figure 3.16 Development of free salicylic acid in aspirin–paracetamol–codeine and aspirin–phenacetin–codeine tablets at 37^oC.

Reproduced from Boggianno BG et al. Aust J Pharm 1970;51:S14.

Other studies on the influence of tablet excipients on drug decomposition have identified problems with stearate salts and it has been suggested that these salts should be avoided as tablet lubricants if the active component is subject to hydroxide ion-catalysed degradation. The degradative effect of the alkali stearates is inhibited in the presence of malic, hexamic or maleic acid owing, it is thought, to competition for the lubricant cation between the drug and the additive acid.

The base used in the formulation of suppositories can often affect the rate of decomposition of the active ingredients. Aspirin decomposes in several polyoxyethylene glycols that are often incorporated into suppository bases.²⁷ Degradation was shown to be due in part to transesterification, giving the decomposition products salicylic acid and acetylated polyethylene glycol. The rate of decomposition, which followed pseudo first-order kinetics, was considerably greater than when a fatty base such as cocoa butter was used.²⁸ Analysis of commercial batches of 100 mg indometacin–polyethylene glycol suppositories²⁹ showed that approximately 2%, 3.5% and 4.5% of the original amount of indometacin was esterified with polyoxyethylene glycol 300 (XV) after storage times of 1, 2 and 3 years, respectively.

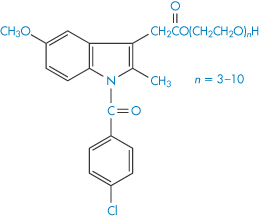
Structure XV Polyethylene glycol esters of indometacin identified in stored suppositories (n = number of ethylene oxide units).

Excipients present in tablet formulations can have an impact on the photostability of the product, the effect arising in many cases from impurities present in the excipients.¹⁰ For example, free radical reactions involving phenolic impurities in tablet-binding agents such as povidone, disintegrants such as crospovidone, and viscosity-modifying agents such as alginates can lead to photodegradation. Similarly, coloured products may be formed by the reaction of aldehydes formed during spray drying or autoclaving of lactose with primary amine groups in the product.

Temperature

Investigation of the effect of temperature change on the stability of solid-dosage forms can be complicated for many possible reasons. The drug or one of the excipients may, for example, melt or change its polymorphic form as temperature is increased, or it may contain loosely bound water that is lost at higher temperatures. We should also remember that the relative humidity will change with temperature and so we must take care to keep this at a constant value.

Despite these possible complications, many authors have found that the effect of temperature on decomposition rate can be described by an Arrhenius-type equation; i.e. plots of log k against 1/T are linear. This then enables the stability to be predicted at room temperature from measurements made at elevated temperatures. Although we can calculate an apparent activation energy, E_a, from the gradient of the plots, we must remember that this does not have the same meaning as the activation energy for reactions in solution. The E_a value in the solid state is affected, for example, by changes not only in the solubility of the drug in the moisture layer but also in the intrinsic rate of reaction. We cannot, however, use the Arrhenius equation in cases where decomposition shows an approach to equilibrium. Examples of such systems include vitamin A in gelatin beadlets and vitamin E in lactose based tablets. In these cases we can often use the van’t Hoff equation to describe the effect of temperature on breakdown. We determine the equilibrium concentrations of products and reactants at a series of temperatures and then plot the logarithm of the equilibrium constant, K, against the reciprocal of the temperature (Fig. 3.17) according to the equation

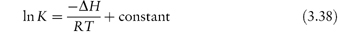
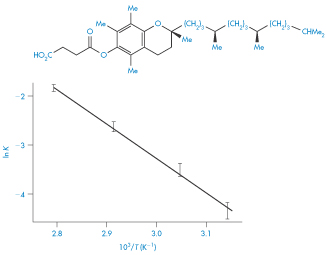
Figure 3.17 Van’t Hoff plot for vitamin E succinate decomposition in lactose base tablets.

Reproduced from Carstensen JT et al. Equilibrium phenomena in solid dosage forms. J Pharm Sci 1968;57:23. Copyright Wiley-VCH Verlag GmbH & Co. KGaA. Reproduced with permission.

Light and oxygen

We have examined above the stability problems that arise with drugs that are susceptible to photodecomposition or oxidation. We will not reconsider them here but merely re-emphasise that we should take all the necessary precautions to exclude light or oxygen when storing these drugs. In this respect we should remember that water contains dissolved oxygen and so the presence of moisture on the surface of solid preparations may increase the oxidation of susceptible drugs; such drugs must, therefore, be stored under dry conditions.

3.5 Stability testing and prediction of shelf-life

It is clearly most important to be able to ensure that a particular formulation when packaged in a specific container will remain within its physical, chemical, microbiological, therapeutic and toxicological specifications on storage for a specified period. In order to make such an assurance, we obviously need to conduct a rigorous stability-testing programme on the product in the form that is finally to be marketed. Since the testing period can be as long as 2 years, it has become essential to devise a more rapid technique that can be used during product development to speed up the identification of the most suitable formulation. In this section we shall examine ways of predicting the chemical stability of a formulation during preformulation studies using accelerated storage tests. We will not be considering the toxicological or microbiological studies or the determination of physical stability, all of which are essential elements in the overall stability testing of the formulation, but which are outside the scope of this chapter. Although most of this section will be concerned with the prediction of the effect of temperature on drug decomposition, other environmental factors will also be briefly considered.

3.5.1 Effect of temperature on stability

We have already considered the basic method of accelerating the chemical decomposition by raising the temperature of the preparations. We shall briefly reconsider essential steps in the process. The order of reaction can be determined by plotting stability data at several elevated temperatures according to the equations relating decomposition to time for each of the orders of reaction, until linear plots are obtained. We can now calculate values of rate constant at each temperature from the gradient of these plots, and plot the logarithm of k against reciprocal temperature according to the Arrhenius equation

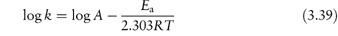
The required value of k can be interpolated from this plot at room temperature, and the activation energy E_a calculated from the gradient, which is −E_a/2.303R. Values of E_a are usually within the range 50−96 kJ mol⁻¹.

A convenient, approximate method that is useful for estimation of decomposition rates at room temperature makes use of the ratio of rate constants at room temperature (T₁) and a higher temperature (T₂). If we subtract the Arrhenius equations at temperatures T₁ and T₂, assuming that the log A term is the same at each temperature, we obtain

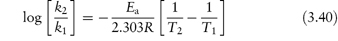
or

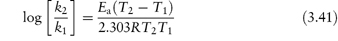
We must, of course, have a value of E_a in order to be able to use these equations for the calculation of the room temperature rate constant k₁. If we only require a rough estimation of k₁ then we can assume a mid-range value of E_a, say 75 kJ mol⁻¹, for these calculations.

An alternative method of data treatment is to plot the logarithm of the half-life, t_0.5, as a function of reciprocal temperature. From equation (3.9), t_0.5 = 0.693/k. Therefore,

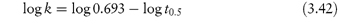
and substituting into equation (3.32) gives

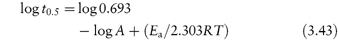
Once the rate constant is known at the required storage temperature it is a simple matter to calculate a shelf-life for the product based on an acceptable degree of decomposition. The equations we can use for 10% loss of activity are obtained by substituting x = 0.1a in the zero- and first-order equations (equations 3.7 and 3.8), giving

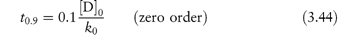
and

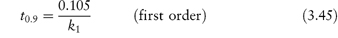
where [D₀] is the initial concentration of drug. Although t_0.9 is usually used as an estimate of shelf-life, other percentage decompositions may be required, for example when the decomposition products produce discoloration or have undesirable side-effects. The required equations for these may be derived by substituting in the relevant rate equations.

Although accelerated storage testing based on the use of the Arrhenius equation has resulted in a very significant saving of time, it still involves the time-consuming step of the initial determination of the order of reaction for the decomposition. While most investigators have emphasised the need for a knowledge of the exact kinetic pathway of degradation, some have bypassed this initial step by assuming a particular decomposition model. At less than 10% degradation and within the limits of experimental error involved in stability studies, it is not possible to distinguish between zero-, first- or simple second-order kinetics using curve-fitting techniques; consequently the assumption of first-order kinetics for any decomposition reaction should involve minimum error. In fact, it was shown that there was a linear relationship between the logarithm of t_0.9 (the time taken for the concentration of the reactant to decompose to 90% of its original value) and the reciprocal temperature, which was independent of the order of reaction for the decomposition of a series of drugs.³⁰ On the basis of these findings it was suggested that the use of such linear plots to determine t_0.9 at the required temperature would provide a rapid, and yet sufficiently accurate, means of studying decomposition rate during the development stage.

Even with the modifications suggested above, the method of stability testing based on the Arrhenius equation is still time-consuming, involving as it does the separate determination of rate constants at a series of elevated temperatures. Experimental techniques have been developed^31,32 that enable the decomposition rate to be determined from a single experiment. Such methods involve raising the temperature of the product in accordance with a predetermined temperature–time programme and are consequently referred to as non-isothermal stability studies. Any suitable temperature–time programme may be used; Derivation Box 3C illustrates the method proposed by Rogers³¹ in which the rise of temperature was programmed so that the reciprocal of the temperature varied logarithmically with time. In this method data are plotted as log f(c) against log(1 + t), where f(c) = 2.303 log (c₀/c_t) and c₀ and c_t are the concentrations at zero time and at time t, respectively. The gradient of this plot is (1 + E_ab/R), where b is any suitable proportionality constant, enabling E_a to be determined. The rate constant k₀ at an initial time T₀ may then be calculated from the intercept when log(1 + t) = 0, which is equal to log k₀ − log(1 + E_ab/R). The rate constant at any other temperature may be calculated from k₀ and E_a.

The advantages of the method shown in Derivation Box 3C over the conventional method of stability testing are that: (a) the data required to calculate the stability are obtained in a single 1-day experiment rather than from a series of experiments that might last for several weeks; (b) no preliminary experiments are required to determine the optimum temperatures for the accelerated storage test; and (c) the linearity of the plot of log f(c) against log(1 + t) confirms that the correct order of reaction has been assumed.

Several improvements on the original non-isothermal stability-testing methods have been suggested. Rather than subjecting the drug formulation to a predetermined fixed time–temperature profile, the temperature may be changed during the course of the experiment at a rate consistent with the analytical results from the experiment.³² The resultant time–temperature data are fitted to a polynomial expression of sufficient degree to describe the changes. This relationship and the experimental data are then combined and used to compute a series of degradation pathways corresponding to a series of values of activation energy. The curves are matched with the experimental analytical data to obtain the correct activation energy for the reaction. Using this activation energy and the analytical data, the reaction rate and stability may be calculated. Computational procedures whereby the activation energy and frequency factor of the Arrhenius equation may be determined from simple non-isothermal experiments with a fixed temperature–time profile have been described.^33,34

An improvement in the design of stability tests has been suggested that avoids the difficulties inherent in the non-linear curve-fitting procedures outlined above.³⁵ The experimental procedure involves changing the temperature of the samples being studied until degradation is rapid enough to proceed at a convenient rate for isothermal studies to be carried out. The analytical information obtained during the non-isothermal and isothermal portions of the experiment is used in calculating the activation energy and determining the order of reaction and the reaction rate and predicting stability at any required temperature.

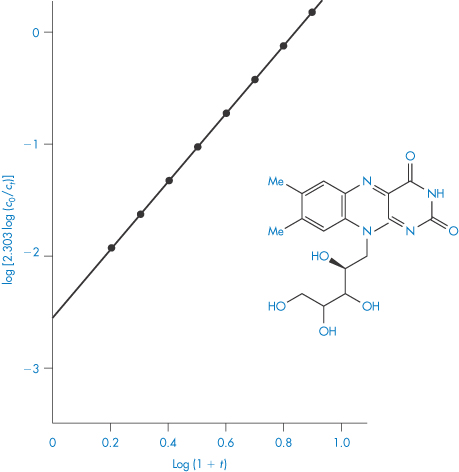
Figure 3.18 Example 3.11: Accelerated storage plot for the decomposition of riboflavin in 0.05 mol dm⁻³ NaOH using data from reference 31.

Although accelerated storage testing has proved invaluable in the development of stable formulations, it is important that we consider some of the limitations of this technique. We must take care that the order of reaction is not different at the higher temperatures from that which occurs at room temperature. There are several cases where this might be so. For example, with complex decomposition processes involving parallel or consecutive reactions, there may be a change in the relative contributions of the component reactions as the temperature is increased.

Suspensions

One complication that arises when we are carrying out stability testing of suspensions is the changes in the solubility of the suspended drug with increase in temperature. With suspensions, the concentration of the drug in solution usually remains constant because, as the decomposition reaction proceeds, more of the drug dissolves to keep the solution saturated. As we have seen, this situation usually leads to zero-order release kinetics. If the actual decomposition of dissolved drug is first-order, then we can express the decrease of concentration, c, with time, t, as

where k₀ = k₁S and S is the solubility of the drug.

The problem that arises with these systems is that an increase of temperature causes not only the usual increase in rate constant, but also an increase in solubility. Application of the Arrhenius equation to the data involves the measurement of the changes in solubility of the drug over the temperature range involved. An alternative method that does not necessitate the determination of solubility uses the relationship between solubility and temperature:

Since k₀ = k₁S,

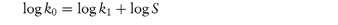
If we substitute for log k₁, using the Arrhenius equation, we obtain

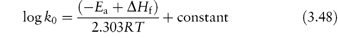
where ΔH_f is the molar heat of fusion. You can now see that we can plot log k₀ against 1/T and extrapolate to give a room temperature value of k₀. It is important we remember that this treatment assumes that drug degradation in solution follows first-order kinetics and that the kinetics are not limited by the dissolution rate.

Solid state

The main problems arising in stability testing of solid-dosage forms are²⁶: (a) that the analytical results tend to have more scatter because tablets and capsules are distinct dosage units rather than the true aliquots encountered with stability studies on drugs in solution, and (b) that these dosage forms are heterogeneous systems often involving a gas phase (air and water vapour), a liquid phase (adsorbed moisture) and the solid phase itself. The compositions of all of these phases can vary during an experiment.

The first of these problems can be overcome by ensuring uniformity of the dosage form before commencing the stability studies. The problems arising from the heterogeneity are more difficult to overcome. The main complicating factor is associated with the presence of moisture. As we have seen in section 3.4.3, moisture can have a significant effect on the kinetics of decomposition and this may produce many experimental problems during stability testing. For example, with gelatin capsules the water in the capsule shell must equilibrate with that in the formulation and surrounding air and this may require an appreciable time. The prediction of stability is difficult in solid-dosage forms in which there is chemical interaction between components, or chemical equilibrium phenomena. In fact, the data for stability studies involving the latter are often plotted using a van’t Hoff plot rather than an Arrhenius plot.

To reduce some of these problems, particularly those associated with moisture, during stability testing, the following have been suggested²⁶: (a) the use of tightly sealed containers, except where the effect of packaging is to be investigated; (b) that the amount of water present in the dosage form should be determined, preferable at each storage temperature, and (c) that a separate, sealed ampoule should be taken for each assay point and water determination, thus avoiding disturbance of water equilibrium on opening the container.

As has been discussed above, we can often use the Arrhenius equation to predict stability in the solid state, even though the kinetics of breakdown are different from those in solution. The exception to this is when equilibrium reactions occur, in which case we can often use the van’t Hoff equation (equation 3.38) to predict room-temperature stability.

3.5.2 Other environmental factors affecting stability

Light

Photostability testing of drug substances usually involves the initial stress testing of the drug to determine its overall photostability and the identification of any degradation products. In this process the sample is irradiated at all absorbing wavelengths using a broad-spectrum light source. Those drugs or formulations that are shown to be photosensitive are then subjected to more formal photostability testing in which they are challenged with light of wavelength comparable to that to which the formulations are exposed in practical situations. During their shelf-life it is most likely that the products will be exposed to fluorescent light, direct daylight and daylight filtered through window glass, and the stability-testing procedures are designed to cover these possibilities. A specific protocol for testing the photostability of new drugs and products is described in the International Conference on Harmonisation (ICH) Guideline.³⁶

Oxygen

The stability of an oxidisable drug in a liquid-dosage form is generally a function of the efficiency of any antioxidant included in the formulation. Exaggeration of the effect of oxygen on stability may be achieved by an increase in the partial pressure of oxygen in the system. It is not often easy, however, to make decisions on what would be the normal access of oxygen during storage and a meaningful extrapolation of the acquired data may be difficult.

Moisture content

The stability of solid-dosage forms is usually very susceptible to the moisture content of the atmosphere in the container in which they are stored (see section 3.4.3) A linear relationship between log k and the water vapour pressure for vitamin A palmitate beadlets in sugar-coated tablets has been found.³⁷ Similarly, a linear relationship has been established between the logarithm of the rate constant for the decomposition of nitrazepam in the solid state and the relative humidity (Fig. 3.19). The need for consideration of the effect of moisture on stability has been stressed by Carstensen,¹⁵ who stated that stability programmes should always include samples that have been artificially stressed by addition of moisture. One purpose of a stability programme should be to define the stability of the dosage form as a function of moisture content.

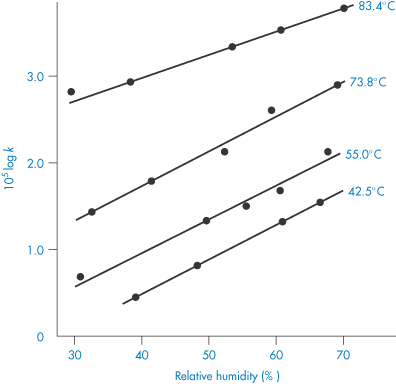
Figure 3.19 Logarithm of the nitrazepam decomposition constant, k, as a function of relative humidity at various temperatures.

Reproduced from Genton D, Kesselring UW. Effect of temperature and relative humidity on nitrazepam stability in solid state. J Pharm Sci 1977;66:676. Copyright Wiley-VCH Verlag GmbH & Co. KGaA. Reproduced with permission.

3.5.3 Protocol for stability testing

A stability-testing requirement for a Registration Application agreed within the three areas of the EC, Japan and the USA exemplifies the core stability data package required for new drug substances and associated drug products.³⁸ Under this agreement, information on stability generated in any one of these three areas that meets the appropriate requirements of this guideline is mutually acceptable in both of the other two areas. The following summarises some of the main points of the guideline as it affects the stability testing of both drug substances and drug products; the original document should of course be consulted if a more detailed account is required.

Drug substances

Stability information from accelerated and long-term testing is required to be provided on at least three batches manufactured to a minimum of pilot plant scale by the same synthetic route and using a method of manufacture and procedure that simulates the final process to be used on a manufacturing scale. In this context, ‘pilot plant scale’ is taken to mean a minimum scale of one-tenth that of the full production process. The containers to be used in the long-term evaluation should be the same as, or simulate, the actual packaging used for storage and distribution. The overall quality of the batches of drug substance subjected to stability testing should be representative of both the quality of the material used in preclinical and clinical studies and the quality of material to be made on a manufacturing scale.

The testing should be designed to cover those features susceptible to change during storage and likely to influence quality, safety and/or efficacy, including, as necessary, the physical, chemical and microbiological characteristics. The length of the studies and the storage conditions should be sufficient to cover storage, shipment and subsequent use. The specifications for the long-term testing are a temperature of 25 ± 2°C and 60% ± 5% relative humidity for a period of 12 months. For accelerated testing the temperature is specified as 40 ± 2°C and 75% ± 5% relative humidity for a period of 6 months. Other storage conditions are allowable if justified; in particular, temperature-sensitive drugs should be stored at a lower temperature, which then becomes the designated long-term testing temperature. The 6-month accelerated testing should then be carried out at a temperature at least 15°C above this designated temperature together with the relative humidity appropriate to that temperature. Where ‘significant change’ occurs during the 6 months’ accelerated storage testing, additional testing at an intermediate temperature (such as 30 ± 2°C/60% ± 5% relative humidity) should be conducted for drug substances to be used in the manufacture of dosage forms tested for long-term stability at 25°C/60% relative humidity. ‘Significant change’ at 40°C/75% relative humidity or 30°C/60% relative humidity is defined as failure to meet the specification.

The long-term testing is required to be continued for a sufficient period of time beyond 12 months to cover all appropriate retest periods. The frequency of testing should be sufficient to establish the stability characteristics of the drug substance; under the long-term conditions this will normally be every 3 months over the first year, every 6 months over the second year, and then annually.

Drug product

The design of the stability programme for the finished product is based on the knowledge of the behaviour and properties of the drug substance and the experience gained from clinical formulation studies and from stability studies on the drug substance. Stability information from long-term and accelerated testing is required to be presented on three batches of the same formulation and dosage form in the containers and closure proposed for marketing. Two of the three batches should be at least pilot-scale; the third batch may be smaller, for example 25 000–50 000 tablets or capsules for solid-dosage forms. Data on laboratory-scale batches are not acceptable as primary stability information. It is stipulated that the manufacturing process to be used should meaningfully simulate that which would be applied to large-scale batches for marketing and should provide product of the same quality intended for marketing, and meeting the same quality specification as to be applied for release of material. Where possible, batches of the finished product should be manufactured using identifiably different batches of drug substance.

As with the stability testing of drug substance, the testing of the product should cover those features susceptible to change during storage and likely to influence quality, safety and/or efficacy. The range of testing should cover not only chemical and biological stability but also loss of preservative, physical properties and characteristics, organoleptic properties and, where required, microbiological attributes.

The conditions and time periods for long-term and accelerated storage testing are the same as those outlined above for drug substances but with special considerations arising from the nature of the drug product. If it is necessary to store the product at a lower temperature because of its heat sensitivity, then consideration should be given to any physical or chemical change in the product that might occur at this temperature; for example, suspensions or emulsions may sediment or cream, while oils and semisolid preparations may show an increased viscosity. Storage under conditions of high relative humidity applies particularly to solid-dosage forms. For products such as solutions and suspensions contained in packs designed to provide a permanent barrier to water loss, specific storage under conditions of high relative humidity is not necessary, but the same range of temperatures should be applied. It is recognised that low relative humidity (10–20%) can adversely affect products packed in semipermeable containers such as solutions in plastic bags and nose drops in small plastic containers, and consideration should be given to appropriate testing under such conditions.

In the case of drug products, ‘significant change’ at the accelerated condition is defined as:

• a 5% potency loss from the initial assay value of a batch
  
• any specified degradant exceeding its specification limit
  
• the product exceeding its pH limits
  
• dissolution exceeding the specification limits for 12 capsules or tablets
  
• failure to meet specifications for appearance and physical properties, e.g. colour, phase separation, resuspendability, delivery per actuation, caking and hardness.

If significant change occurs at 40°C/75% relative humidity then it is necessary to submit a minimum of 6 months’ data from an ongoing 1-year study at 30°C/60% relative humidity using the same criteria for ‘significant change’.

Summary

In this chapter we have examined the various ways in which drugs can chemically break down in both liquid and solid-dosage forms and discussed possible means of preventing or minimising this loss of activity. The most common cause of degradation of drugs in aqueous solution is the hydrolysis of groups such as esters, amides, lactones, lactams, imides or carbamates. The stability of solutions of drugs containing these groups can be improved by formulation at the pH of maximum stability. Care must be taken, however, in the choice of buffer used because hydrolysis is catalysed not only by hydrogen or hydroxyl ions (specific acid–base hydrolysis) but also by the components of buffer solutions (general acid–base catalysis). Drugs possessing carbon–carbon double bonds, such as the steroids, polyunsaturated fatty acids and polyene antibiotics, are susceptible to oxidative degradation; liquid formulations of these drugs may be stabilised by replacing the oxygen in the system with inert gases such as nitrogen; by avoiding contact with metals such as iron, cobalt and nickel; and by adding antioxidants or reducing agents to the solution. Some oxidative reactions are pH-dependent, in which case the product can be stabilised by buffering the system. Other less common types of drug decomposition include photochemical breakdown (necessitating storage in amber containers), epimerisation and polymerisation.

We have seen how reactions may follow zero-, first- and second-order kinetics and examined how to determine the rate constant, and in some cases the half-life, of the decomposition process. With this information we are able to make a prediction of the shelf-life of the product, which is usually the time taken for the drug to be reduced to 95% of its original potency. Although the breakdown of most drugs in solution follows first-order or pseudo first-order kinetics, the decomposition process may be complicated by more complex breakdown schemes involving parallel, reversible or consecutive reactions.

Assessment of the optimum pH for formulation of liquid-dosage forms is greatly speeded up by measuring the hydrolysis rate at a series of elevated temperatures and extrapolating to room temperature using the Arrhenius equation. A protocol for stability testing that has been agreed in the EC, Japan and the USA has been described.

The kinetics of drug decomposition in solid-dosage forms is less well understood. Decomposition of drugs susceptible to hydrolysis can occur if moisture is allowed to adsorb on to the surface of the dosage form and the packaging should be selected to minimise this effect. Excipients of the solid-dosage form can affect drug breakdown by increasing the moisture content of the dosage form. Film coating of tablets can markedly reduce moisture ingress, as discussed in Chapter 1.

Some final points on the stability of drugs

Given that the explicit aim of an understanding of the stability of drug molecules is to ensure the quality of medicines and to avoid the presence of toxic and other degradants, is it worth remembering the wide relevance of stability at various stages of drug development and use.

• It is important at the drug discovery stage to ensure that drugs injected into animals or tissues in culture are indeed stable in the medium used in pharmacology laboratories, where the media used may have suboptimal pH for drug solubility or stability. This is to ensure that the drug being studied is indeed the one intended.
  
• It is, of course, vital that different routes of synthesis of new (and established) molecules are evaluated in terms of which route produces the purest molecules with minimal impurities caused by side-reactions or residual solvents and catalysts.
  
• Many protein-based therapeutics have complex pathways of production, discussed briefly in Chapters 13 and 16; these molecules can be fragile and suffer not only chemical instability but also physical (such as conformational) instabilities.
  
• There are many possibilities for drugs to interact with formulation components, as we have discussed; there are examples of drugs such as doxorubicin interacting with components of microspheres and nanoparticles, or reacting with chemicals such as glutaraldehyde used in the preparation of, for example, albumin microspheres. Sadly, in these days where counterfeiting is becoming a greater problem not only in the developing world but also in Europe, the analysis of drug content and quality can often distinguish those drugs which are genuine and those which are counterfeit. Often it is the impurity profile which provides the fingerprint to aid detection.

Historical examples of instability, interactions and adverse effects are very much worthy of study as they can aid us in predicting the likelihood of these events with novel drug molecules. This requires us, as we point out in the Introduction to this book, to have a feeling for the chemistry of drugs and thus the ability to extrapolate sensibly from known scenarios to new and uncertain cases.

References

1. LePree JM, Connors KA. Hydrolysis of drugs. In: Swarbrick J (ed.) Encyclopedia of Pharmaceutical Technology, 3rd edn. New York: Informa Healthcare; 2006: 2040–2047.

2. Wells PR. Linear free energy relationships. Chem Rev 1963;63:171–219.

3. Cartensen JT et al. Use of Hammett graphs in stability programs. J Pharm Sci 1964;53:1547–1548.

4. Hovorka SW, Schöneich C. Oxidative degradation of pharmaceuticals: theory, mechanisms and inhibition. J Pharm Sci 2001;90:253–269.

5. Johnson DM, Taylor WF. Degradation of fenprostalene in polyethylene glycol 400 solution. J Pharm Sci 1984;73:1414–1417.

6. Halbaut L et al. Oxidative stability of semi-solid excipient mixtures with corn oil and its implication in the degradation of vitamin A. Int J Pharm 1997;147:31–40.

7. Smith GB et al. Autooxidation of simvastatin. Tetrahedron 1993;49:4447–4462.

8. Lamy-Freund MT et al.  Effect of aggregation on the kinetics of autoxidation of the polyene antibiotic amphotericin B. J Pharm Sci 1993;82:162–166.

9. Manjappa AS et al. Is an alternative drug delivery system needed for docetaxel? The role of controlling epimerization in formulations and beyond. Pharm Res 2013;30:2675–2693.

10. Tønnesen HH. Formulation and stability testing of photolabile drugs. Int J Pharm 2001;225:1–14.

11. Greenhill JV, McLelland MA. Photodecomposition of drugs. Prog Med Chem 1990;27:51–121.

12. Huang CL, Sands FL. Effect of ultraviolet irradiation on chlorpromazine. II. Anaerobic condition. J Pharm Sci 1967;56:259–264.

13. Matsuda Y et al. Stabilization of sulfisomidine tablets by use of film coating containing UV absorber: protection of coloration and photolytic degradation from exaggerated light. J Pharm Sci 1978;67:196–201.

14. Bundgaard H. Polymerization of penicillins: kinetics and mechanism of di- and polymerization of ampicillin in aqueous solution. Acta Pharm Suec 1976;13:9–26.

15. Carstensen JT. Stability of solids and solid dosage forms. J Pharm Sci 1974;63:1–14.

16. Carstensen JT. Drug Stability. Principles and Practices, 2nd edn. New York: Marcel Dekker; 1995.

17. Andersin R, Tammilehto S. Photochemical decomposition of midazolam. IV. Study of pH-dependent stability by high-performance liquid chromatography. Int J Pharm 1995;123:229–235.

18. Torniainen K et al. The effect of pH, buffer type and drug concentration on the photodegradation of ciprofloxacin. Int J Pharm 1996;132:53–61.

19. Ong JTH, Kostenbauder HB. Effect of self-association on rate of penicillin G degradation in concentrated aqueous solutions. J Pharm Sci 1975;64:1378–1380.

20. Allen AE, Das Gupta V. Stability of hydrocortisone in polyethylene glycol ointment base. J Pharm Sci 1974;63:107–109.

21. Das Gupta V. Effect of vehicles and other active ingredients on stability of hydrocortisone. J Pharm Sci 1978;67:299–302.

22. Busse MJ. Dangers of dilution of topical steroids. Pharm J 1978;220:25.

23. Ullmann E et al. The stability of sodium penicillin G in the presence of ionic surfactants, organic gel formers, and preservatives. Pharm Acta Helv 1963;38:577–586.

24. Testa B, Etter JC. Hydrolysis of pilocarpine in Carbopol hydrogels. Can J Pharm Sci 1975;10:16–20.

25. Poust RI, Colaizzi JC. Copper-catalyzed oxidation of ascorbic acid in gels and aqueous solutions of polysorbate 80. J Pharm Sci 1968;57:2119–2125.

26. Tingstad J, Dudzinski J. Preformulation studies. II. Stability of drug substances in solid pharmaceutical systems. J Pharm Sci 1973;62:1856–1860.

27. Jun HW et al. Decomposition of aspirin in polyethylene glycols. J Pharm Sci 1972; 61:1160–1162.

28. Whitworth CW et al. Stability of aspirin in liquid and semisolid bases. II. Effect of fatty additives on stability in a polyethylene glycol base. J Pharm Sci 1973; 62:1372–1374.

29. Ekman R et al. Formation of indomethacin esters in polyethylene glycol suppositories. Acta Pharm Suec 1982;19:241–246.

30. Amirjahed AK. Simplified method to study stability of pharmaceutical preparations. J Pharm Sci 1977;66:785–789.

31. Rogers AR. An accelerated storage test with programmed temperature rise. J Pharm Pharmacol 1963;15:101T.

32. Maudling HV, Zoglio MA. Flexible nonisothermal stability studies. J Pharm Sci 1970;59:333–337.

33. Madsen BW et al. Integral approach to nonisothermal estimation of activation energies. J Pharm Sci 1974;63:777–781.

34. Kay AI, Simon TH. Use of an analog computer to simulate and interpret data obtained from linear nonisothermal stability studies. J Pharm Sci 1971;60:205–208.

35. Zoglio MA et al. Nonisothermal kinetic studies III: rapid nonisothermal–isothermal method for stability prediction. J Pharm Sci 1975;64:1381–1383.

36. ICH Harmonised Tripartite Guideline. Q1B: photostability testing of new drug substances and products. Federal Register 1997;62:27115.

37. Lachman L. Physical and chemical stability testing of tablet dosage forms. J Pharm Sci 1965;54:1519–1526.

38. Note for Guidance on Stability Testing: Stability Testing of New Drug Substances and Products (ICH). CPMP/ICH/2736/99. London: Medicines Control Agency; 1999 (adopted 2003).

Stay updated, free articles. Join our Telegram channel

Join