Fig. 4.1
Histological sections of an elastic artery fixed in a physiological condition, stained with hematoxylin-eosin (nucleus, purple) and Azan-Mallory (smooth muscle, red; collagen, blue; unstained, elastin)
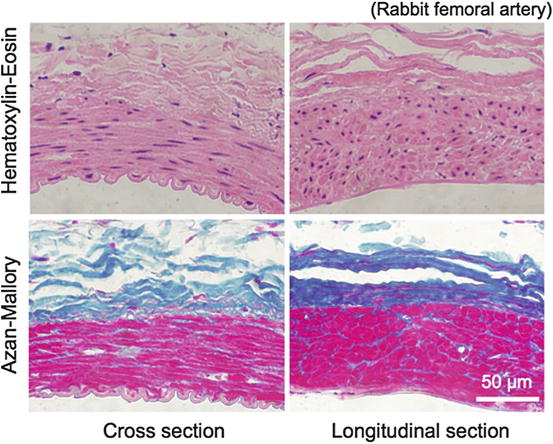
Fig. 4.2
Histological sections of a muscular artery fixed in a physiological condition, stained with hematoxylin-eosin (nucleus, purple) and Azan-Mallory (smooth muscle, red; collagen, blue; unstained, elastin)
From the viewpoint of biomaterials, blood vessel wall can be viewed as a composite material consisting of components with various mechanical properties such as elastin, collagen, and smooth muscle cells. Elastin is highly elastic material with Young’s modulus of ~500 kPa [2–4]. It remains elastic at least until its length is doubled (Fig. 4.3). Compared to elastin, collagen is highly stiff material with Young’s modulus of ~1 GPa (Fig. 4.4) [5, 6]. Although collagen fibers can bear high stress in the body, they are less deformable and become fractured at relatively low strain (less than 10 %). In case of artery wall, they align obliquely to stretch direction and are corrugated in a physiological state. Such oblique alignment and corrugation allow the artery walls large deformation (~100 %) in the physiological condition as well as their strain-hardening properties (see Sect. 4.2.1.1 for details). In contrast to elastin and collagen that behave mostly linearly elastic materials, smooth muscle cells are highly viscoelastic. Their mechanical properties change drastically depending on their contractile state. Their Young’s modulus ranges from 10 kPa under relaxation to 100 kPa under contraction (Fig. 4.5) [7]. Smooth muscle cells also have a unique characteristic, i.e., mechanical adaptation. They change their dimensions and mechanical properties in response to mechanical stimulation they receive to maintain homeostasis of intramural mechanical environment (see Sect. 4.4.2 for details).
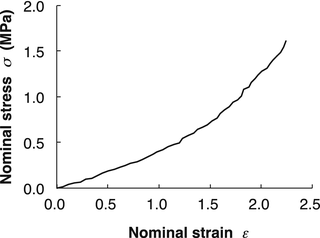
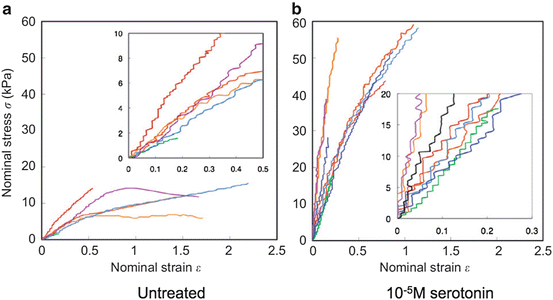

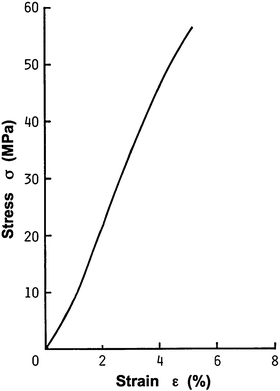
Fig. 4.3
Stress-strain relationship of an elastic lamina (porcine thoracic aorta). Nominal stress-strain curve is almost linear until nominal strain exceeds 1.0, i.e., until the length is doubled

Fig. 4.5
Tension-elongation relationship of vascular smooth muscle cells obtained from rabbit thoracic aorta. Smooth muscle contraction was induced with serotonin (Reprinted from Ref. [7], Copyright 2012, with permission from Elsevier)
The mechanical properties of the vascular wall are determined by relative amount of these components, their alignment, and their slackness, etc. The aorta, an elastic artery, is abundant in elastin and the largest artery. Due to its abundance in elastin and its large size, the aorta is the most compliant vessel in the vascular system. It expands in response to blood pressure increase in systole to store a part of the blood pumped out from the heart and thus helps to decrease the systolic pressure, i.e., the load of the heart. In diastole, it shrinks in response to pressure decrease to maintain distal blood flow just like an air-pressurized reservoir in a water gun (Windkessel effect). As one goes from proximal to distal side, the diameter and wall thickness of the artery decrease monotonously, and the relative amount of smooth muscle cells and the ratio of collagen to elastin increase. Because collagen is much stiffer than elastin, distal arteries are generally stiffer than the proximal arteries. The collagen to elastin ratio continues to increase in the veins. The veins have larger diameter and thinner wall compared to arteries at the same anatomical position. Because they occupy about 3/4 of the total vessel volume and show large deformation in the physiological condition, the veins serve as a reservoir of the blood that controls the circulating blood volume and called a capacitance vessel. Veins in the extremities have valves to prevent regurgitation. Blood vessel network from the arterioles to venules via capillaries is called a microcirculatory system. The microcirculatory system is called a resistance vessel for it is the major part of resistance in the circulatory system. The arterioles with abundant smooth muscle cells are responsible for the maintenance of the blood pressure by changing their diameter by smooth muscle contraction and relaxation.
4.2 Mechanics of Blood Vessel
4.2.1 Basic Characteristics
Blood vessel walls are exposed to various mechanical stresses in vivo. In case of artery wall, its intraluminal surface is subjected to mean pressure of ~13.3 kPa (100 mmHg) and pulse pressure of ~5.3 kPa (40 mmHg). Arterial walls are stretched by 30–50 % in the longitudinal direction, which can be confirmed by arterial contraction in the longitudinal direction after excision. Wall shear stress of a few Pa is applied to the intraluminal surface due to the blood flow, and wall shear stress oscillates during the cardiac cycle. Due to these mechanical stresses, the artery diameter changes by ~10 % and its length changes by a few % during the cardiac cycle. Twisting of the vessel is very small [8].
In case of the veins, quasistatic pressure of ~1.3 kPa is applied to the walls. The intraluminal pressure sometimes has a negative value due to the pressure difference between veins and the heart and/or due to other physical forces from the surrounding tissues. Under these circumstances, outer radius of the veins can change by several tens of percent.
From the mechanical point of view, keywords expressing basic characteristics of the blood vessel walls are as follows: (1) large deformation and nonlinear mechanical properties, (2) incompressibility, (3) viscoelasticity, and (4) anisotropy. Details of each characteristic are described in the following sections.
4.2.1.1 Large Deformation and Nonlinear Mechanical Properties
The vascular walls undergo large deformation, and its physiological strain ranges from several tens of percent to 100 %. Mechanical properties such as elasticity depend on the magnitude of pressure applied to the vessel walls significantly. Arterial wall shows remarkable strain-hardening properties. It is quite deformable in subphysiological pressure range, while in supraphysiological pressure range, it becomes less deformable sharply as pressure increases. This means that we need to pay attention to strain or pressure levels when comparing elastic moduli between blood vessels. For example, in rabbit thoracic aortas, when pressure increases from 2.7 kPa (20 mmHg) to 23.9 kPa (180 mmHg), their circumferential stretch ratio increases from 1.1 to 2.0, and an incremental elastic modulus E inc (see Sect. 4.2.2 for details) increases from 200 kPa to 8,200 kPa by 40 times (Table 4.1).
Table 4.1
Pressure dependence of incremental elastic modulus of the rabbit thoracic aortas
Pressure (mmHg) | Incremental elastic modulus (kPa) |
|---|---|
20 | 200 ± 20 |
50 | 200 ± 10 |
100 | 430 ± 30 |
125 | 1,550 ± 150 |
150 | 4,480 ± 360 |
180 | 8,200 ± 720 |
Nonlinearity of the stress-strain relationship of blood vessels can be explained by the degree of undulation and variation of alignment of collagen fibers in the vessel walls. Both elastic and collagen fibers in the fiber direction have linear mechanical properties. As described in Sect. 4.1, Young’s modulus of elastin is ~0.5 MPa and that of collagen fibers is ~1 GPa. In low-pressure region, collagen fibers remain wavy (Fig. 4.6) and align obliquely to the circumferential direction [9], while elastic fibers are straight, and thus, the incremental elastic modulus is low (Table 4.1). In high-pressure region, stiff collagen fibers become straight and begin to be stretched [10], resulting in the strain hardening of the blood vessel wall. Since collagen fibers are not stretched in low-pressure region, breaking strain of the aorta (~100 %) is in the range between breaking strain of elastin (~200 %) [2] and that of collagen (~10 %) [5]. The strain-hardening property of the blood vessel is very important for the arteries to prevent vessel rupture (see Sect. 4.3.1 for details).
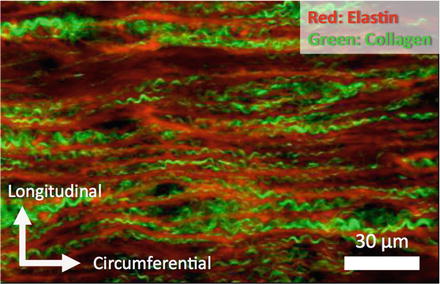

Fig. 4.6
Corrugation of collagen fibers in a rabbit thoracic aorta pressure-fixed at 80 mmHg
4.2.1.2 Incompressibility
Generally speaking, soft biological tissues are mainly composed of water. For example, water content of canine arterial walls is around 70 % of total volume [11]. Because water is incompressible, i.e., does not change its volume during deformation, the artery wall is also considered to be incompressible. Carew et al [12] measured the volumetric change of dog thoracic aortas during inflation-extension test. They found that volume strain was only 0.06 % when 40 and 70 % of strain were imposed in longitudinal and circumferential direction, respectively.
4.2.1.3 Viscoelasticity
Viscoelastic materials exhibit not only elastic characteristics but also viscous when undergoing deformation. Elastic materials deform when stretched and quickly return to their original state once the stress is removed. Viscous materials deform linearly with time when a stress is applied. Viscoelastic materials have elements of both of these properties and, as such, exhibit time-dependent strain. The effect of viscoelasticity on mechanical properties of large blood vessels is relatively small. Change in the stiffness due to change in strain rate could be several 10 % at most. Therefore, large vessels are often treated as elastic tubes. However, it should be noted that effects of viscoelasticity could be much larger and cannot be ignored in small arteries. For further discussion, see Sect. 4.2.3.
4.2.1.4 Anisotropy
Major constituents of blood vessels such as collagen, elastin, and smooth muscle cells predominantly orient in the circumferential-longitudinal plane. Since mechanical properties of arteries depend on the properties of the individual constituents and their orientations, mechanical properties in the radial direction are different from the circumferential and longitudinal directions. Even in the circumferential-longitudinal plane, anisotropy has been observed. Uniaxial tensile test has shown that the tensile strength of the aortas is larger in the circumferential direction than in the longitudinal direction [13]. In a bulge test, in which a platelike specimen is sandwiched with two plates having a hole at their center and pressurized from one side, porcine thoracic aortas initiated cracks in the circumferential direction [14]. Pressure-imposed tests for tubular specimens have indicated that the difference in an elastic modulus is at most twofolds for large arteries [15]. However, because most of the blood vessels are tethered in the longitudinal direction and their compliance is mostly determined by the deformability in the circumferential direction, the mechanical properties in the circumferential direction, i.e., pressure-diameter relationship, which is important from a practical standpoint.
4.2.2 Parameters Expressing Mechanical Properties of Blood Vessel
To obtain detailed mechanical properties of blood vessels, we excised them from bodies and loaded them with a wide range of pressure to obtain pressure-diameter relationship with an apparatus shown in Fig. 4.7, for example. A quasistatic and dynamic pressure-diameter curve of canine common carotid artery is shown in Fig. 4.8 [16]. The pressure-diameter curve shows characteristics of the nonlinear and downward-convex relationship as described in Sect. 4.2.1. These characteristics are seen in both arteries and veins. It also has a hysteresis as shown in the difference between the loading and unloading limbs. The hysteresis is derived mainly from viscoelasticity of smooth muscle cells. The area of the hysteresis loop depends on the relative volume and the activity of smooth muscle cells.
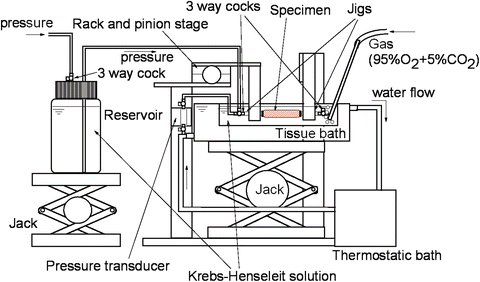
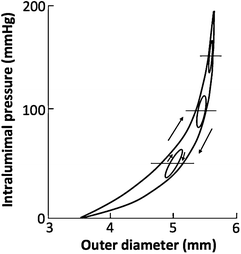

Fig. 4.7
An example of experimental setup for the measurement of pressure-diameter relationship of blood vessels. To mimic physiological condition, specimen was immersed in an aerated Krebs-Henseleit solution at 37 °C and pressurized pneumatically while measuring its outer diameter with a video camera and a video dimension analyzer (not shown)

Fig. 4.8
Pressure-diameter relationship of a canine common carotid artery. The large nonlinear hysteresis loop is obtained in a quasistatic condition, i.e., by changing the intraluminal pressure at the rate of ~1 mmHg/s. Small oval loops are obtained in a dynamic condition, i.e., by changing intraluminal pressure sinusoidally at ~1 Hz (Reprinted from Ref. [16], with permission from JSME)
Stiffness of blood vessels can be measured from the pressure-diameter curve. It is affected by not only Young’s modulus but also the geometry of the vessels such as radius and wall thickness. For example, for two cylindrical tubes made of the same material (i.e., with the same Young’s modulus) with the same outer radius, one with thicker wall is stiffer. Similarly, two tubes made of the same material with the same wall thickness, one with smaller radius is stiffer. Thus, we need to evaluate stiffness and elastic modulus separately.
Although the pressure-diameter curves are highly nonlinear in a wide range of pressure, each of them can be regarded as linear if you divide them into small sections. Then elastic modulus can be defined using a linear equation. When pressure increases from P i by ΔP i and outer diameter from D o by ΔD o, elastic modulus and stiffness can be calculated from P i, D o, and ΔD o /ΔP i. In the following part of this section, some of the representative parameters expressing mechanical properties of the blood vessel are introduced.
4.2.2.1 Incremental Elastic Modulus E inc
The incremental elastic modulus, E inc, which corresponds to Young’s modulus of blood vessel wall can be expressed by the following equation [17]:
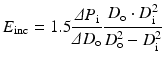
To calculate the incremental elastic modulus, the inner diameter D i or wall thickness, which is difficult to measure in clinical practices, is needed. This parameter is used mainly in experimental studies for excised specimens, but not for clinical medicine. Usually inner diameter D i is calculated from inner and outer diameters d i and d o, respectively, at no-load state under the assumption of incompressibility of vessel wall as follows:
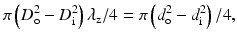
where λ z is a longitudinal stretch ratio, which is defined as the ratio of the in vivo length of a vessel segment L to its length at no-load state l, i.e., λ z = L/l.
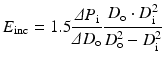
(4.1)
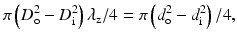
(4.2)
4.2.2.2 Pressure Strain Elastic Modulus E p
The pressure strain elastic modulus, E p, presenting stiffness of blood vessel can be expressed by the following equation [18]:
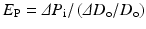
Since it can be easily calculated from obtained data in clinical practice, it has been used widely not only in experimental studies but also in clinical medicine.
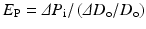
(4.3)
4.2.2.3 Stiffness Parameter β
The stiffness parameter β can be expressed by the following equation:
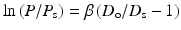
where P s and D s are pressure and outer diameter, respectively, at a reference state in vivo [19]. Normally reference state is taken as P s = 100 mmHg (13.3 kPa). It is well known that pressure-diameter curve of an artery is well fitted by an exponential function. This parameter is obtained based on this knowledge, and the nonlinearity of blood vessels can be eliminated at least partially in the physiological range, i.e., it is relatively insensitive to the variation of blood pressure. And also, this parameter does not require blood vessel wall thickness that is difficult to measure in clinical practices. Thus, the stiffness parameter has been widely used in clinical medicine.
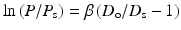
(4.4)
Typical values of these parameters are summarized in Table 4.2 for various species and anatomical sites.
Table 4.2
Normal values for parameters expressing elastic properties of blood vessels of various species and anatomical sites [16]
Blood vessel | E inc a (MPa) | E p b (MPa) | β |
|---|---|---|---|
Thoracic aorta | 0.5 (D), 0.9 (R) | 0.07 (H) | 2.5 (R) |
Abdominal aorta | 1.0 (D), 2.0 (R) | 0.10 (H) | 5.6 (H) |
Common carotid artery | 0.9 (D), 1.5 (R) | 0.08 (H) | 5.3 (H) |
Femoral artery | 1.0 (D), 4.0 (R) | 0.49 (H) | 19.8 (H) |
Pulmonary artery | 0.6 (D) | ||
Coronary artery | 1.7 (D) | 29.8 (R) | |
Arteriole | 0.12 (CM) | ||
Capillary | 0.37 (CM) | ||
Venule | 0.39 (CM) | ||
Saphenous vein | 0.03 (D) | ||
Jugular vein | 1.5 (D) | ||
Inferior vena cava | 0.07 (D) |