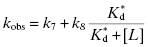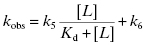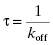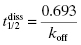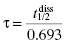The second type of system is termed an open system. This case is more reflective of how drugs and targets encounter one another in vivo. Here one of the components (i.e., the target) is held within a defined container (e.g., a cell) at a fixed concentration. The other component (most commonly, the drug) flows into the container harboring the target, diffuses within the container to encounter the target, and may also flow out of the container by passive and/or active transport mechanisms. For example, when a drug that targets an intracellular enzyme is administered orally, it must enter the gastrointestinal tract, be absorbed from the intestines into systemic circulation, be thus transported to the tissue of interest, diffuse through the tissue to reach the cell, be transported into the cell, and then diffuse to the enzyme before association (binding) can occur. Once bound, the drug can dissociate from the enzyme and may rapidly rebind, due to the high local concentration of drug in the immediate proximity of the enzyme. Alternatively, the dissociated drug molecule may diffuse through the cell interior (i.e., the cytosol or other subcellular compartments), and eventually be transported back out of the cell (Figure 8.1). Within and outside of the cell, various chemical (e.g., digestion) and metabolic processes (see Chapter 10) may degrade or transform the drug to eliminate it from the body. Hence, in contrast to the constant concentration encountered in a closed system, the open system is characterized by continuous changes in the flux of drug available for encounter with the target. Because the free concentration of drug is continuously in flux in an open system, equilibrium measurements are no longer appropriate. Measurement of the rate constant for binary complex association may be possible, but in many cases this is compromised by other processes that limit access of the drug to the target (see below). On the other hand, the dissociation rate for the binary drug–target complex is first-order and thus independent of any changes in free drug concentration.
Let us consider further the fate of a drug molecule in an open, in vivo system. Suppose that a drug is dosed orally to achieve a maximum concentration in systemic circulation of 1 μM (see Chapter 10). The association rate constant for a drug binding to its target is second-order, and varies over a range of ca. 106 to 108 M−1s−1. At a concentration of 1 μM (i.e., 1 × 10−6 M), the half-life for drug association would thus be on the millisecond time scale. Even the slowest of association rates would be very rapid on the time scale of the biological processes (e.g., intestinal absorption, tissue distribution) that limit drug access to the target; these biological processes typically take tens of minutes or longer, thus conferring a significant limitation on the rate of bimolecular encounters between drug and target. Thus, in open system biology, the microscopic rate constant for bimolecular association is no longer the main determinant of complex formation, hence pharmacologic effect.
There are several other reasons to focus attention on the dissociative process as a portent of in vivo drug effectiveness. First, despite the variability seen in association rate constants for biological drug–target pairs (as well as for receptor–ligand pairs in general), the association rate is always ultimately limited by the rate of diffusion of the two binding partners in physiological solution. For a small (ca. 500 Daltons) molecule drug binding to a macromolecular target (ca. 50 kDa), the diffusion limit puts an upper boundary on the association rate constant of ca. 107–109 M−1s−1 (Fersht, 1999). While in principle, medicinal chemistry efforts could be focused on accelerating the rate at which slow-binding drugs reach their targets, there is no mechanism available to the medicinal chemist to overcome the diffusion limit. Second, the physicochemical steps involved in drug–target association, such as diffusion, desolvation, and molecular orbital orientation, are difficult for medicinal chemists to affect in any systematic way. Attempts to impact these steps through structure–activity relationships (SAR) are therefore purely empirical in nature. Third, the rate of drug association with the target depends not only on the bimolecular association rate constant (kon), but also on the concentration of the drug. Thus, a small value of kon can often be compensated for by merely increasing the drug concentration (i.e., the dose).
The dissociation rate constant (koff), on the other hand, is independent of pharmacological factors, such as absorption and distribution rates, and is also independent of the local concentration of free drug. Rather, koff is entirely dependent on specific interactions between the drug and its target binding pocket. The interaction forces that determine drug dissociation rates are the same familiar forces that are commonly associated with thermodynamic affinity: protein conformation, hydrogen bonding, hydrophobic interactions, van der Waals forces, and the like. Optimization of these interaction forces, and consequently of the dissociation rate, is the sine qua non of medicinal chemistry as applied to the iterative process of SAR studies.
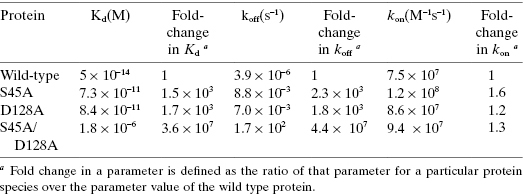
Indeed, it is often the case that SAR studies that are guided by IC50 or Ki measurements in closed, in vitro systems (see Chapter 5) principally lead to optimization of residence time (i.e., dissociation rate), although this is usually unrecognized by the experimenters. An excellent example of this comes from the work of Hyre et al. (2006) on the interactions of biotin with the protein streptavidin. The steptavidin–biotin complex is one of the highest affinity protein–ligand complexes known, with a Kd value of ca. 5 × 10−14 M. In the crystal structure of the binary streptavidin–biotin complex it is clear that the side chains of serine 45 and aspartic acid 128 make key hydrogen bonds with the ligand. Mutation of either of these residues to alanine significantly reduced the binding affinity of the protein for biotin, and mutation of both residues to alanine had an even more dramatic effect. These authors also measured the kinetics of biotin association with and dissociation from the various streptavidin forms. They found, as summarized in Table 8.1, that all of the changes in binding affinity (i.e., Kd) could be associated with changes in dissociation rate (i.e., residence time; vide infra) with essentially no change in association kinetics.
TABLE 8.1 Thermodynamic and Kinetic Factors for Biotin Binding to Streptavidin Mutants
Source: Data from Hyre et al. (2006).
It might thus be argued that the need for optimization of residence time is already fulfilled by standard in vitro assay measurements, and there is no need for more complete assessment of both Ki and koff values. Two points are worth noting in this regard. First, optimization of Ki and koff values are not always convergent within the SAR of a particular pharmacophore series, and especially among different pharmacophore series. Simultaneous modifications of both kon and koff can therefore result in compounds displaying similar Ki values but vastly different koff values (Swinney, 2011). Second, the measurement of Ki values alone, without accompanying evaluation of koff, provides no assessment of the temporal components of efficacy (i.e., duration of action) and target selectivity (vide infra), which could be of critical importance in the open system of in vivo pharmacology.
Thus, the overarching hypothesis that we set forth in this chapter is that durable in vivo pharmacology in driven largely by the residence time of the binary drug-target complex, and that residence time is most dependent on the dissociation rate constant koff, rather than the equilibrium constant Kd per se. We therefore postulate that the residence time of a drug–target complex in vivo is best assessed quantitatively by measurement of the reciprocal of the binary complex dissociation rate constant in vitro (1/koff). In the following sections we shall explore the basis for this hypothesis and the experimental data that support it.
8.2 The Static View of Drug-Target Interactions
As described above and in Chapter 6, a static view of drug–target interactions has predominated biochemistry and pharmacology for nearly 100 years. This view envisages the enzyme active site (or other ligand binding pockets of macromolecular targets) as structurally fixed, such that drug, or other ligand, affinity is dictated by steric and electrostatic complementarity with the rigid architecture of the binding pocket, thus creating a network of favorable interactions between the drug and recognition elements within the binding pocket. In this manner, the binary drug–target complex is stabilized relative to the free reactants (i.e., drug and target; Copeland, 2000, 2011; see Figure 8.2):
Figure 8.2 Cartoon of reversible receptor–ligand binding for the static, one-step binding and dissociation model of interaction. The rate constants k3 and k4 refer to the association and dissociation rate constant for this model, respectively. Note that the numbering convention for individual rate constants throughout this chapter follows that established in Chapter 6.
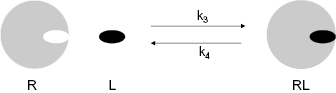
In this diagram, R is the free receptor (i.e., target), L is the free ligand (i.e., drug), and RL is the binary complex. In this mechanism, k3 is equivalent to kon and k4 is equivalent to koff (Note: We are using the same numbering convention for kinetic rate constants here as was established in Chapter 6). As discussed in Chapter 6, this conventional view further considers the recognition elements of the binding pocket to be held static in the most complementary arrangement with respect to ligand interactions. Hence, drug association and dissociation each occur in a single kinetic step, and the efficiency of interaction may be quantified by familiar, mathematically–related parameters such as IC50 values, Kd values, and ΔGbinding (Copeland, 2000). Although Kd and ΔGbinding are thermodynamic constants, they can be readily related to the kinetic rate constants for drug association and dissociation as follows (Copeland, 2000).
(8.1)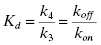 
(8.2)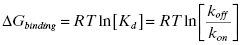 
For weak binding interactions (i.e., Kd values in the μM to mM range), association and dissociation are usually rapid, with half-lives on the μs timescale. This rapidity of binding and dissociation can be important for physiological reactions, such as enzymes binding to substrates and cofactors (Fersht, 1999). As binding affinity increases, however, it is often the case that the rates of association and especially of dissociation slow down to timescales of seconds, minutes, and sometimes longer; hence, these reactions may be conveniently measured in vitro by a number of biochemical and biophysical methods (Schreiber et al., 1985a, b; Morrison and Walsh, 1988; Copeland, 2000; Copeland et al., 2006; Hulme and Trevethick, 2010).
Using convenient experimental methods, one can mix a macromolecular target (let us refer to these universally as receptors and use the symbol R to represent them) with a drug or other ligand (we will use the symbol L to universally represent these molecules) and measure the amount of binary complex (RL) formed as a function of time after mixing. In most experimental approaches to measuring receptor–ligand binding, the receptor concentration is held constant at a very low, limiting concentration relative to that of the ligand. Under these conditions, the binding of the ligand to the receptor follows pseudo-first-order kinetics (see Appendix 1) and the approach to equilibrium can therefore be described by a pseudo-first order rate constant kobs.
As we saw in Chapter 6, the value of kobs depends on the concentration of ligand in characteristic ways that can be mechanistically informative (Jarv et al., 1979; Morrison and Walsh, 1988; Tummino and Copeland, 2008). For the simple, static binding mechanism illustrated in Figure 8.2, the value of kobs is a linear function of ligand concentration for which the slope is equal to the value of kon and the intercept is equal to the value of koff.
There are indeed examples of drug–target complexes for which this type of binding measurements yields a linear plot of kobs as a function of ligand concentration (see, e.g., the data for MMP2 inhibition shown in Figure 6.13 of Chapter 6). Hence, in these cases the experimental data are consistent with single step binding and dissociation, and therefore a static drug binding pocket. These cases are not common, however, and often it turns out that there are conformational adjustments to the binding pocket that attend ligand binding. In such cases the thermodynamic stability of the protein conformers are similar and therefore interconversion among conformers occurs too rapidly to be observed in standard binding experiments. This was the case, for example, in studies of piperidine inhibitors of the aspartyl protease pepsin (Marcinkeviciene et al., 2002).
8.3 Conformational Adaptation in Drug–Target Interactions
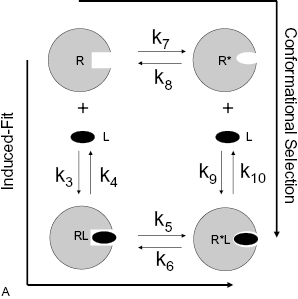
Despite being commonly found in textbooks, the static model of drug–target interactions (vide supra) is seldom adequate to describe fully the association and dissociation of high-affinity drugs with their targets. For the majority of drugs that bind with nanomolar or lower Kd values, it is common to find conformational adjustments of the drug binding pocket that attend complex formation (Jarv et al., 1979; Copeland, 2000, 2010, 2011; Copeland et al., 2006; Tummino and Copeland, 2008; Swinney, 2004, 2011). This type of conformational adaptation can result from two kinetic pathways for drug association that have been referred to as the conformational selection and induced-fit models of binding (Koshland, 1958; Morrison and Walsh, 1988; Boehr et al, 2009; Hammes et al., 2009; Figure 8.3; see also Chapter 6).
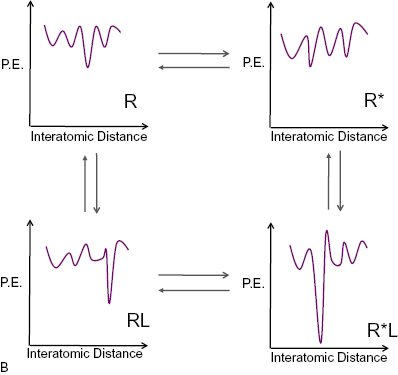
Figure 8.3 (A) Cartoon illustrating the conformational selection (clockwise) and induced-fit (counter-clockwise) models of bimolecular interactions between receptors and ligands. (B) Idealized potential energy diagrams for the four states associated with the conformational selection and induced fit models. P.E., potential energy.
8.3.1 Conformational Selection Model
In the conformational selection model the target exists in an ensemble of conformers in the absence of a drug (i.e., ligand); only some of these conformers are capable of binding ligand. For simplicity, let us say that the ensemble of conformers is composed of only two states that are in equilibrium with one another: a state that is unable to bind ligand (R) and an alternative conformer that does bind ligand (R*). In the absence of ligand, the equilibrium strongly favors the R state over the R* state, and interconversion between these states is relatively slow. On addition of ligand, those receptor molecules in the R* conformer will bind ligand (R*L) and therefore be removed from the equilibrium between the free forms R and R*. This leads to a shift in the equilibrium position to favor formation of more R*, which can then bind more ligand until, at infinite ligand concentration, the entire system has shifted to the R*L state (Figure 8.3). In this model the rate limiting step in binding is assumed to be interconversion between the two free forms R and R*; once formed, R* binds ligand rapidly.
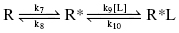
In this model, k7 represents the rate constant for receptor isomerization from R to R* prior to ligand binding, and k8 represents the rate constant for the reverse isomerization step. As only conformational state R* has significant affinity for ligand in this model, the equilibrium dissocation constant,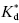 
, is defined here by the ratio k10/k9.
8.3.2 Induced-Fit Model
The induced-fit model (Figure 8.3) results in the same final form of the drug-target complex, R*L, but arrives at this state through a different kinetic pathway. Here the unbound receptor exists in a single conformational state, R, that is capable of binding ligand to form an encounter complex, RL. The recognition elements within the binding pocket are not optimally complementary to ligand in the RL state. The act of ligand binding causes a conformational readjustment of the target to form a new conformation (R*L) in which optimal complementarity between ligand and binding pocket is achieved. In this model, ligand binding to the initial encounter state, R, is considered rapid and the rate-limiting step is a slow conformational transition (i.e., isomerization) from the RL state to the final R*L state.
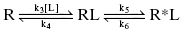
Here the initial binding event is controlled by forward and reverse rate constants k3 and k4 (such that, as in the static, one-step binding and dissociation model, the Kd for the encounter complex (RL) is defined by the ratio k4/k3). Subsequent to binding, the receptor isomerizes to the new species R*L with rate constant k5, and this conformational transition is reversed with rate constant k6. As described in Chapter 6, the overall equilibrium binding constant,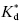 
, in this model reflects the affinity of the final R*L state and is equivalent to Kd/(1 + k5/k6).
An important point to bear in mind is that for both models, each target conformer (R, R*, RL, and R*L) represents an ensemble of conformational microstates that may interconvert through vibrational, rotational, and translational excursions, depending on the energy barrier to interconversion (i.e., there is microscopic reversibility among states). Hence, stabilization of a particular state, such as a ligand-bound state, depends on populating a deep, narrow potential energy well that creates a substantial energy barrier to escape and thus to interconversion. It is also important to realize that the conformational selection and induced-fit models merely represent opposite poles of a continuum of conformational adaptation mechanisms that nature may use to promote molecular recognition between binding partners (Hammes et al., 2009; Bhabha et al., 2011). A final point that is worth mention is that the conformational selection and induced-fit models are thermodynamically indistinguishable. That is, the overall binding affinity in both models will depend on the free energy difference between the starting and ending states of the system. By what kinetic path the system arrives at the final state is irrelevant from a thermodynamic perspective (i.e., the free energy of binding is a path-independent parameter).
8.3.3 Kinetic Distinction Between Conformational Selection and Induced-Fit Mechanisms
The conformational selection and induced-fit models may be experimentally distinguished by measurements of the pseudo-first order rate constant for approach to equilibrium as a function of ligand concentration, as first encountered in Chapter 6. Equations describing the dependence of kobs on ligand concentration for the two mechanisms have been independently derived by multiple investigators and are well established in the biochemical literature. One finds that the quantitative value of kobs varies with ligand concentration in opposing fashions for the two mechanisms (Chapter 6). For the conformational selection mechanism kobs depends on ligand concentration as described by the following equation (Duggleby et al., 1982; Auzat et al., 1995; Tummino and Copeland, 2008; Weikl and von Deuster, 2009):
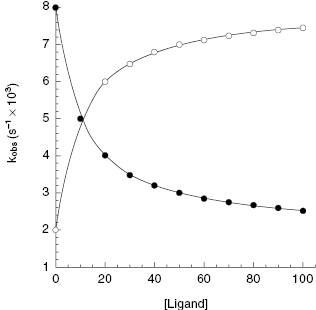
where k7 is the rate constant for forward isomerization from state R to R*, k8 is the rate constant for the reverse isomerization from R* to R, and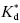 
is the equilibrium dissociation constant for the R*L binary complex (Figure 8.3A). As we saw in Chapter 6, the limits of kobs at zero and infinite ligand concentrations can be determined by inspection of Equation (8.3). When [L] is zero, kobs reduces to (k7 + k8), and when [L] is infinite kobs reduces to k7. Thus the value of kobs decreases curvilinearly with increasing ligand concentration from an intercept value of (k7 + k8) to a final value of k7 at infinite ligand concentration (Figure 8.4).
Figure 8.4 The dependence of kobs on ligand (i.e., inhibitor) concentration expected for the conformational selection (closed circles) and induced-fit (open circles) models of bimolecular interaction.
For the induced fit model, kobs depends on ligand concentration as follows.
The limits at zero and infinite concentration from Equation (8.4) are k6 and (k5 + k6), respectively. Thus, for the induced-fit model kobs is a saturable, hyperbolic function of ligand concentration, increasing from an intercept value of k6 to a final value of (k5 + k6) at infinite ligand concentration (Figure 8.4).
This type of experiment provides a clear and unambiguous basis for defining the mechanism of interaction that is germane to a specific drug–target pair. In this manner, the two mechanisms of conformational adaptation in drug binding are readily distinguished from one another.
As discussed in Chapter 6, most high-affinity drugs bind to their targets through a conformational adaptation mechanism. Hence, one may ask which of the two conformational adaptation models presented above is most germane for drugs binding to their macromolecular targets. In fact, examples of both mechanisms can be found in the literature, based on the type of kinetic analysis just described. Table 8.2 provides examples of drugs or drug-related compounds for which either a conformational selection or induced-fit model may be invoked on the basis of kinetic data. Note that the entries in Table 8.2 for conformational selection represent all examples of this mechanism that are known to the author from survey of the literature. In contrast, the entries for induced-fit represent a sampling of a much larger pool of known examples of this mechanism.
TABLE 8.2 Some Examples of Receptor–Ligand Binding Interactions for Which a Conformational Selection or Induced-Fit Mechanism Has Been Demonstrated
Source: Data Taken from Copeland (2011).
| Mechanism | Target | Ligand(s) |
|---|---|---|
| Conformational selection | Human glucokinase | Glucose |
| Rat liver glucokinase | Glucose | |
| α-chymotrypsin | Proflavin | |
| E. coli alkaline phosphatase | 2,4-dinitrophenyl phosphate | |
| Ribtonuclease T1 | Guanosine 3′-GMP | |
| Protein Kinase A | PLN1-20 | |
| Induced-fit | Cyclooxygenase-2 | DuP697 NS-398 |
| Cyclooxygenase-1 | Idomethacin | |
| Purine nucleoside phosphorylase | DADMe-ImmH DADMe-IMMG | |
| Xanthine oxidase | Allopurinol | |
| Mycobacterium tuberculosis enoyl reductase | Isoniazid | |
| Dihydrofolate reductase | Methotrexate | |
| Hepatitis C virus NS3 protease | ITMN-191 VX-950 | |
| HIV-1 protease | Darunivir | |
| Prostate-specific antigen | Phosphoramidate peptidomimetics | |
| HSP90 | Geldenamycin | |
| Bacterial β-ketoacyl-acyl carrier protein synthases | Thiolactomycin | |
| HIV-1 Integrase | Elitegravir Raltegravir GSK364735 | |
| Aurora B | GSK1070916 | |
| AKT | GSK690693 | |
| Steroid 5α-reductase | Finasteride Dutasteride | |
| Bacterial ribosome | Erythromycin Retapamulin | |
| HIV reverse transcriptase | Efavirenz | |
| Glu-tRNAGln amidotransferase | Boronate-peptidomimetics | |
| Polypeptide deformylase | Actinonin | |
| Kinesin motor protein | Ispinesib | |
| Bacterial deacetylase LpxC | Ciprofloxacin | |
| HMG CoA reductase | Rosuvastin | |
| Lipoxygenase-1 | Amidrazine | |
| Calcineurin | L-732531 | |
| Xylanose | ABTI | |
| Nitric oxide synthase | 1400W | |
| BACE | Statine peptidomimetic | |
| p38 MAP kinase | BIRB796 | |
| Dialkylglycine decarboxylase | Aminophosphonates |
Reviewing the information summarized in Table 8.2, all of the examples of conformational selection are for enzymes, mainly binding to natural substrates or cofactors. In the overwhelming majority of cases of a drug molecule binding to a macromolecular target, the binding appears to conform to an induced-fit mechanism. Thus, while both mechanisms appear to be applicable to receptor–ligand binding in general, pharmacologic modulation of targets appears to most often involve an induced-fit mechanism of conformational adaptation.
8.4 Impact of Residence Time on Natural Receptor–Ligand Function
Open biological systems, as defined above, create high hurdles for the specificity and stability required of receptor–ligand mediated biological functions. Ligand concentrations at the receptor site change over time, and in some cases, the ligand is not colocalized with the receptor at the cellular or tissue level. Additionally, some multistep biosynthetic functions have a strict requirement for fidelity, and open systems increase the already high entropic barrier that exists in these cases (see below). In many cases, biological systems employ prolonged receptor–ligand residence time, varying across a wide range, as one method of overcoming these hurdles. Below, we exemplify these concepts with descriptions of selected classes of receptor–ligand complexes for which residence time is a clear and important component of biological function (Tummino and Copeland, 2008).
8.4.1 Immune Response
Adaptive immune response involves the formation of binary complexes between ligands and receptors on B and T lymphocytes. Antigen receptors, composed of immunoglobulin domains, on the surface of B-cells recognize and bind specific antigens such as proteins from pathogenic bacteria and viruses. The receptor–antigen complex on the B-cell surface undergoes endocytosis and intracellular proteolytic processing to produce antigen-derived peptides. These peptides are then presented on the surface of the B-cell in complex with a protein of the major histocompatibility complex (MHC) class II. The peptide–MHC complex (pMHC) then acts as a ligand for the T-cell receptor (TCR), in concert with the CD4 coreceptor, on the surface of T-helper cells. Engagement of TCR/CD4 by the pMHC leads to T-helper cell activation, resulting in cytokine secretion that stimulates a number of cellular responses, including B-cell proliferation and thus specific antibody production. In a like manner, the TCR on killer T-cells, together with its coreceptor CD8, engages antigen–MHC class I complexes on cell surfaces, stimulating secretion of cytotoxins by the killer T-cell. The cytotoxins target the plasma membrane of the antigen-presenting cell, resulting in apoptotic cell death.
Several studies have explored the kinetics of interactions between various components of the adaptive immune system. Among a large number of studies of soluble antibody–antigen interactions, some common features emerge (Janin and Chothia, 1990). Often, association of the antibody with the antigen is slower than expected for a diffusion-controlled process, and this has been suggested to result from a two-step, induced-fit mechanism of binding (vide supra). Dissociation of antibody–antigen complexes is generally found to be slow, with residence times ranging from minutes to days or longer. For example, Katsamba et al. (2006) studied the binding of prostate specific antigen (PSA) with several antibodies in a number of independent laboratories. The average value of kon was 4.1 × 104 M−1 s−1, and the values of koff translated into an average residence time of 6.2 hours for these complexes. Several studies comparing on-rate, off-rate, and biological function among various antibodies for a common antigen have shown that optimal function is often correlated with off-rate or residence time. VanCott et al. (1994), for example, looked at a panel of human and mouse antibodies specific for the V3 loop of the HIV-1 envelope glycoprotein gp120. These workers found that the variation in kon across the antibody panel was only 4-fold, while the values for koff varied more than 100-fold. The concentration-dependent ability of the antibodies to neutralize viral replication was also assessed by measuring the concentration of antibody required to inhibit cellular p24 production by 50% (N50 value). A plot of koff and N50 showed a significant correlation between these values (R2 = 0.75; p < 0.001), while a similar plot of kon and N50 demonstrated no correlation (R2 = 0.002; p < 0.92). This is typical of the results seen for other antibody-antigen complexes, with kon values ranging from 104 to 107 M−1s−1 and residence times ranging from a few seconds to several months.
Likewise, the kinetics of interaction between antigens and B-cell surface receptors have been studied by several groups. With respect to recognition specificity, Foote and Eisen (1995) point out that the most rapid association between antigens and B-cell receptors is limited by the diffusion coefficients of the reactants, which puts an upper limit on kon of ca. 106 M−1s−1 for monomeric protein antigens. Since structural complementarity has no impact on diffusion-controlled processes, the encounter rate cannot be a factor in discrimination among antigens. As with soluble antibodies, however, there are experimental data to suggest that antigen binding to B-cell receptors occurs through a two-step, induced-fit process (see Cho et al., 2005, for a summary of these data). Once an antigen is bound at the B-cell receptor, the complex must be internalized through endocytosis to elicit a downstream immune response. If the antigen dissociates from the receptor prior to endocytosis, complex formation cannot elicit a functional response. Hence, immune response requires some minimum residence time for the antigen–receptor complex (Guermonprez et al., 1998). On the other hand, a residence time for the antigen–receptor complex that is much longer than the time required for endocytosis does not provide a further functional advantage. Foote and Eisen (1995) estimated the half-life for endocytosis to be 8.5 minutes. They assumed that two to three half-lives define an upper limit beyond which increased complex stability offers no additional advantage. Hence, the effective limit of B-cell receptor–antigen residence time can be estimated to be between 0.5 and 3 hours. Within this residence time window, Guermonprez et al. (1998) presented data to suggest that the efficiency of B-cell–mediated presentation of antigenic peptides to T-cells is controlled by the off-rate of the antigen–receptor complex, with slower off-rates correlated with an increased level of signaling. Thus, complex stability, dictated by residence time, is a critical factor for ensuring that the binding of antigens to the B-cell receptor translates into functional processing of the antigen.
Once antigen is proteolytically processed within the B-cell, the resulting peptides must form stable, noncovalent complexes with MHC proteins on the surface of the B-cell, to facilitate recognition by the TCR for subsequent T-cell activation. Again, the residence time of the pMHC binary complex is critical to further immune response. The pMHC binary complex exists in an open system in serum with the TCR on T-cells. A long residence time for the pMHC binary complex is important in overcoming the entropic barrier to formation of the pMHC complex–TCR ternary complex. Margulies et al. (1993) studied the kinetics of interactions of MHC class I and II with antigen-derived peptides. The residence times of the pMHC binary complexes ranged from 3 hours to 12 days. These long residence times ensure that the peptide–MHC binary complex endures for sufficient time to affect TCR engagement. Binding of the pMHC to the TCR also appears to proceed through a two-step, induced-fit mechanism, characterized by slow association kinetics, large heat capacity changes, and a large entropic barrier to binding (Cho et al., 2005). These results are bolstered by comparisons of the crystallographic structures of unliganded and pMHC-bound TCRs, which also suggest significant conformational adjustments attending pMHC binding. For example, Boniface et al. (1999) found that the large heat capacity changes that attend pMHC binding to TCR, and a large contribution of conformational entropy to the overall entropic barrier to binding, could not be ascribed to rigid-body association between the binding partners. Rather, the data are indicative of an induced-fit mechanism of binding. These authors go on to suggest that for pMHC–TCR interactions, recognition specificity is not due to rigid alignment of preexisting, complementary surfaces but instead requires unstructured regions of the protein(s) in the free state to fold upon binding to create key parts of the recognition contact interface.
In general, the residence time of the pMHC-TCR complex directly correlates with the degree of T-cell activation. Krogsgaard et al. (2003), however, noted that there are exceptions to this generality. In a detailed study of binding kinetics and thermodynamics, these workers demonstrated for a single TCR interacting with a series of pMHCs that the degree of T-cell activation could be accurately predicted by taking into account both the half-life of the pMHC–TCR complex and the change in heat capacity upon binding. These data suggest that the combination of induced fit and the consequent longer residence time of the complex is a critical factor for the specificity and effectiveness of interactions of pMHC with the TCR.
8.4.2 Control of Protease Activity by Natural Inhibitors
Protease-catalyzed hydrolysis of specific peptide bonds in proteins and peptides is essential for a broad range of physiological functions, including digestion, immune response, xenobiotic metabolism, blood clotting, wound healing, and tissue remodeling. Intracellular proteolysis, due to the action of proteases, plays important roles in processes such as signal transduction, exocytosis, endocytosis, and apoptosis. As essential as these activities are to life, the uncontrolled activity of proteolytic enzymes would be devastating to the organism. Hence, nature has developed several strategies to ensure that these enzymes remain inactive until needed for specific cellular or extracellular functions. A common strategy for inactivating proteases in nature is to form high-affinity, long-lasting binary complexes between the protease and a protein-based inhibitor. Indeed, the residence times for binary complexes between proteases and protein-based inhibitors are among some of the longest found in nature, reflecting the need for tight control of protease activity in vivo. Janin and Chothia (1990) surveyed the structures and binding kinetics for a representative set of 15 pairs of protease–inhibitor complexes. Generally, the contact interface for the complex consisted of a long groove formed by the active site and specificity pockets of the protease and an extended loop of the inhibitor that fits into the protease groove. The contact areas for the complexes range from 600 to 1000 Å2 and are dominated by nonpolar residues. Among these 15 protease–inhibitor complexes, there was little variation in the association rate constants; affinity changes and inhibitor specificity were instead dictated by the dissociation rate constants (koff). The residence times among these complexes range from 1 second for low-affinity complexes to 4 months for the most stable complexes. Further analysis of kinetic data from the literature suggests that association is likely to result from a loose encounter complex that isomerizes to a stable structure with proper packing interactions at the protein interface. The authors noted that experimental evidence for two-step binding mechanisms had been reported from kinetic studies of a number of protease–inhibitor pairs. One of the best-studied examples of a natural protein-based protease inhibitor is pancreatic trypsin inhibitor (PTI), an inhibitor of trypsin and related serine proteases. In a detailed study of binding kinetics, Vincent and Lazdunski (1972) measured the association and dissociation rate constants for trypsin with PTI and for derivatives of each protein. PTI was studied in its natural form and also after selective reduction of the intramolecular disulfide bond between S14 and S38, after reduction and carboxymethylation, and after reduction and carboxamidomethylation. These forms were complexed with natural trypsin, with trypsin that had been selectively reduced and carboxymethylated at S179–S203, and with a catalytically inactivated form of trypsin termed pseudotrypsin. Among these pairs of protease–inhibitor combinations, the association rate constants varied only 55-fold, from 2 × 104 to 1.1 × 106 M−1s−1. In contrast, the values of koff spanned a range of 105-fold, corresponding to residence times from 22 minutes to 6 months. Thus, overall complex lifetime is determined almost exclusively by dissociation rate for protease–inhibitor complexes, such as the trypsin–PTI complex. Likewise, residence time appears to be an important factor in enzyme–inhibitor specificity for these systems as well.
A final example of the impact of residence time on protease–inhibitor stability and specificity comes from studies of tissue inhibitors of metalloproteases (TIMPs) interacting with various soluble and membrane-bound metalloproteases. There are four TIMPs (TIMP-1 to TIMP-4) that are responsible for controlling the activity of a range of metalloproteases. TIMPs were first isolated as complexes with soluble metalloprotease such as matrix metalloproteases 2 and 9 (MMP-2 and MMP-9, respectively). Subsequently, an accumulation of data has suggested that the TIMPs may be unique regulators of type I transmembrane metalloproteases (MTMMPs) and that this is their key physiological role. Several studies of the kinetics of interaction between TIMPS and MMPs and MT-MMPs quantitatively support this suggestion. For example, TIMP-2 binds to MMP-2 and MMP-9 with Ki values of 7.2 and 43.4 nM, respectively (Olson et al., 1997). In contrast, TIMP-2 binds with much greater affinity to MT-1 MMP and MT-3 MMP, displaying Ki values of 0.07 and 0.17 nM, respectively (Zhao et al., 2004). Among these four enzymes, the residence times varied from 7 minutes (for MMP-9- TIMP-2) to 1.4 hours (for MT-1 MMP- TIMP-2). Different TIMPs also appear to regulate different MT-MMPs based on variations in residence time among the complexes. Zhao et al. (2004) compared the binding of TIMP-2, TIMP-3, and TIMP-4 to MT-1 MMP and MT-3 MMP. TIMP-2 was found to be the highest-affinity inhibitor of MT-1 MMP, with a Ki value of 0.07 nM, while TIMP-3 was the best inhibitor of MT-3 MMP (Ki = 0.008 nM). Among the six combinations of enzyme and inhibitor pairs, the values of kon were virtually indistinguishable, ranging only from 1.27 to 3.41 × 106 M−1 s−1 (i.e., a range of<3-fold). What distinguished these complexes from one another were the residence time values, which ranged from 0.46 to 9.7 hours. The residence time differences noted in this paper led the authors to suggest that TIMP-3 is the most likely candidate to act as an MT-3 MMP inhibitor under physiological conditions.
8.5 Impact of Drug–Target Residence Time on Drug Action
8.5.1 Mathematical Definition of Residence Time for Different Mechanisms of Drug–Target Interaction
As described in Chapter 6 for enzyme–inhibitor complexes, and expanded in this chapter for general drug–target pairs, there are a number of mechanisms of drug association that ultimately lead to optimized complementarity, hence optimized binding affinity between the drug and its target binding pocket. Regardless of the association pathway, the definition of drug–target residence time remains the same: the lifetime of the binary drug–target complex.
An experimental measure of residence time is provided by the reciprocal of the macroscopic rate constant for drug–target complex dissociation (koff) and given the symbol tau (τ). The residence time can also be directly related to the dissociative half-life (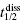
) as follows:
Although the definitions provided by Equations (8.5)–(8.7) are always correct, the relationships between the terms koff, residence time, and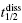 
and the microscopic rate constants for drug binding, target isomerization, and the like depend on the specific mechanism of drug–target engagement. Table 8.3 expands on the presentation from Chapter 6 to provide mathematical definitions for the equilibrium and kinetic constants associated with the one-step binding and dissociation, induced-fit, and conformation selection mechanisms of drug–target interaction.
TABLE 8.3 Mathematical Definitions of Equilibrium and Kinetic Constants for Different Mechanisms of Drug–Target Interactions
source: Adapted from Tummino and Copeland (2008).
Thus, while the residence time (τ) is always equated with the reciprocal of the dissociation rate constant (koff), we see from Table 8.3 that the contributions of various microscopic rate constants to koff, hence to τ, are quite distinct among the mechanisms of drug–target interaction. The additional constituents to koff from the rate constants associated with forward and reverse target isomerization in the induced-fit mechanism contribute to the overall pathway of both drug binding and drug escape; this results in double transition state barriers associated with induced-fit dissociation, as will be described below. The need to surmount two sizable transition state barriers for drug exodus can lead to greatly prolonged drug occupancy, hence durable pharmacology (vide infra), depending on the free energy differences among the states along the escape trajectory.
8.5.2 Impact of Residence Time on Cellular Activity
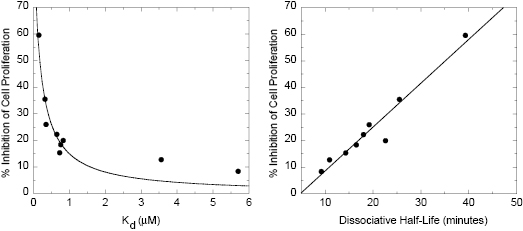
Once a drug enters a cell, one might expect that target occupancy and its resultant impact of phenotypic effects would be directly related to drug–target binding affinity. Yet experimentally one finds a number of cases in which cellular activity is better correlated with residence time than with the equilibrium dissociation constant (Kd). A good example of this comes from the work of Berezov et al. (2001). These workers studied a series of peptides that bind to an extracellular domain of the human epidermal growth factor receptor HER2/neu and disable the tyrosine kinase activity of this receptor. The kinetics of receptor binding and dissociation were measured for nine peptides using surface plasmon resonance technology. The same nine peptides were also tested for their capacity to inhibit cellular proliferation in T6–17 cells at a fixed concentration of 1 μg/mL. Berezov et al. (2001) found that the capacity of the peptides to inhibit cellular proliferation demonstrated a reasonable correlation with Kd values, but a much better correlation with residence time. The data obtained by Berezov et al. (2001) are replotted in Figure 8.5. It is clear from this figure that the percent inhibition of cell proliferation is most highly correlated with residence time. The authors of this work offered no explanation for these observations. Nevertheless, the data demonstrate clearly the significant influence of residence time on the cellular impact of bioactive compounds.
Figure 8.5 Percent inhibition of T6-17 cell proliferation by peptide inhibitors of the HER2 receptor as a function of inhibitor Kd (left) and dissociative half-life (right).
Figure redrawn from Copeland et al. (2006) and based on data from Berezov et al. (2001).
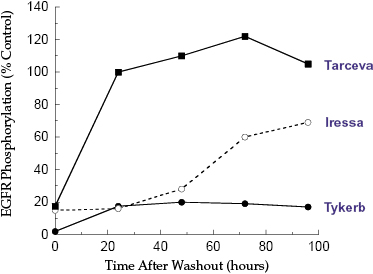
A long residence time on an intracellular target would be expected to translate into sustained effect in cell culture after the removal of the drug supply from the extracellular medium. Assays in which drug is removed from cell culture and the kinetics of recovery of a phenotypic effect (e.g., recovery from inhibition of proliferation) are measured are commonly referred to as “washout experiments.” A salient example of the effects of residence time on such washout recovery comes from the work of Wood et al. (2004) on inhibitors of the epidermal growth factor receptor (EGFR) tyrosine kinase activity. These workers measured the Kd values, the koff values and the recovery of cellular EGFR autophosphorylation after washout for three inhibitors of EGFR that display similar potency in closed-system cellular assays: Lapatinib (Tykerb, GlaxoSmithKline: GW572916), Gefitinib (Iressa, AstraZeneca: ZD-1839), and Erlotinib (Tarceva, OSI: OSI-774). All three drugs are ATP-competitive inhibitors of EGFR, but display maximal affinity for different conformational states of the enzyme. The koff and residence time for all three drugs were determined by recovery of enzymatic activity after jump-dilution (Chapter 5 and below). As seen in Figure 8.6, enzymatic activity was rapidly recovered after dilution with Gefitinib and Erlotinib, suggesting that the residence time of these compounds was relatively short (<10 minutes). In stark contrast, Lapatinib showed very slow recovery of enzymatic activity after dilution, with an estimated residence time of ca. 7 hours (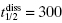
minutes). The authors next measured the recovery of EGFR autophosphorylation activity in a squamous cell head and neck carcinoma line, HN5, after treating the cells for 4 hours with one of the three drugs and subsequent drug washout. The Tarceva treated cells regained full activity (i.e., equal to untreated control cells) witin 24 hours of drug washout. Likewise, significant autophosphorylation activity was recovered after washout of Gefitinib: within 72 hours of washout, the cells treated with Gefitinib recovered 60% of control cell EGFR autophosphorylation activity. Lapatinib, however, was again distinct from the other two EGFR inhibitors in that only 15% of control activity was recovered at 96 hours after drug washout.
Figure 8.6 Recovery of cellular EGFR autophosphorylation after washout of different EGFR inhibitors, as indicated.
Figure constructed from data reported by Wood et al. (2004).
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
