where
dm/dt = solute dissolution rate (kg · s−1)
m = mass of dissolved material (kg)
t = time (s)
A = surface area of the solute particle (m2)
D = diffusion coefficient (m · s−1), which is related, in part, to the viscosity of the solvent, and will be discussed further below.
d = thickness of the concentration gradient (m)
Cs = particle surface (saturation) concentration (kg or moles/L)
Cb = concentration in the bulk solvent/solution (kg or moles/L).
Key Point
Solubility is an endpoint representing dissolution capacity. Dissolution rate can be expressed using the Noyes–Whitney equation.
In this model, Cs is the saturation concentration of the solute in question in the given solvent. The intrinsic dissolution rate (kg · m−2 · s) is the dissolution rate of a pure solute, normalized to the solute surface area, and actually decreases with time. The Noyes–Whitney equation is illustrated in Figure 3.1.
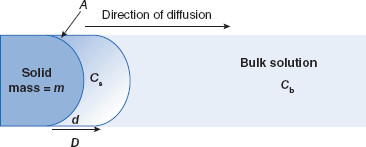
Figure 3.1 Noyes–Whitney parameters for dissolution rate
Dissolution (with rate dm/dt) occurs from a solid with mass = m and surface area = A, from the saturation concentration at the particle surface (Cs) to the concentration in the bulk solution (Cb). Concentration follows a gradient d with a coefficient D.
The Noyes–Whitney equation provides much practical information relevant to the dissolution process. When we look at the equation parameters, we see the equation predicts the following:
• The diffusion coefficient, D, which is in part related to solvent viscosity, will decrease with increasing solvent viscosity, and decreasing dissolution rate, dm/dt. That is, D is inversely proportional to viscosity; D will be discussed shortly.
• Dissolution rate (dm/dt) will be faster with smaller particles because surface area (A) increases as particle size decreases. So, trituration or micronization of particles will usually speed up dissolution.
• Some type of stirring or agitation during dissolution will decrease the diffusion gradient (d) by removing solute molecules more quickly from the particle surface, increasing dissolution rate, dm/dt.
• If the solute is ionizable and/or a weak electrolyte, altering the solvent pH can affect the surface/saturation concentration, Cs. Depending on the characteristics of the solute and solvent, this change could either increase or decrease Cs, either decreasing or increasing the concentration gradient, respectively, and increase or decrease dissolution rate, respectively.
Solubility is a key point, representing capacity. Dissolution rate can be expressed using the Noyes–Whitney equation.
Parameters that affect total solubility
I. The nature and strength of solute–solvent attractions (intermolecular interactions)
II. Polarities of the solute and solvent
III. The thermodynamics of the dissolution
IV. Temperature
V. Ionization of solute and solvent, and pH of the solvent
I. The nature and strength of solute–solvent attractions (intermolecular interactions)
First, the perspective will be changed to that of the solvent. For the sake of discussion, it will be assumed the drug is present as a crystalline structure. Therefore, for this section, the opposite of dissolution is crystallization. The attraction of the solvent for solute molecules (adhesive forces) is in opposition to the attraction of solute molecules to themselves (cohesive forces), and these opposing actions can be represented using an equilibrium equation (Figure 3.2).

Figure 3.2 Dissolution equilibrium
If the solvent sufficiently interacts with solvent particles, the solute intermingles with the solvent. The crystalline structure of the solute is reduced and separated by the solvent into individual ions, atoms or molecules. This process can be visualized in Figure 3.3.
Key Point
Dissolution is a thermodynamically favorable process. In order for a solute to dissolve in a solvent, the process must be thermodynamically favorable.
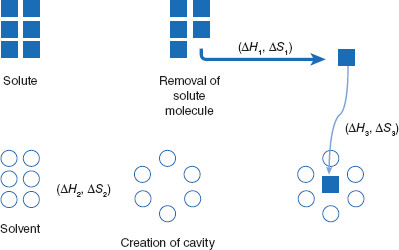
Figure 3.3 Conceptual visualization of dissolution
The dissolution process can be viewed as three thermodynamic steps: 1) creation of an opening (cavity) within solvent molecules with the Gibbs free energy change of ∆H1 and entropy change of ∆S1; 2) removal of a solute molecule from a particle (∆H2, ∆S2); and 3) insertion of the particle into the solvent cavity (∆H3, ∆S3).
In the initial step, the solute is removed (attracted away from) its crystal. Following this, a space is created in a group of solvent molecules and the isolated solute molecule is inserted into this space. Since the solute molecules open to create a space for the solute molecule, the size or surface area of the solute molecule is important. Solute molecules must contact the solute, so large solute molecules will have a smaller surface area for solvent contact than will smaller molecules when considered as a whole. Therefore, solubility tends to decrease with increasing molecular surface area.
II. Polarities of the solute and solvent
The influences of polarity of the solute and solvent were discussed in Chapter 1 in terms of molecular dipoles – innate or induced. If the solvent contains polar molecules (e.g., water), polar solutes will be more attracted to the solvent than will nonpolar solutes. Nonpolar solutes will have some attraction to polar molecules, via dipole–induced dipole actions, but the magnitudes of these attractions will be much smaller. Therefore, polar solutes will generally be more soluble in polar solvents.
III. The thermodynamics of the dissolution
Recall the Gibbs free energy equation, ∆G = ∆H − T∆S, where ∆G is the change in Gibbs free energy (energy to do work), ∆H is the change in enthalpy, and ∆S is the change in entropy. Increases in enthalpy are thermodynamically unfavorable when taken alone, whereas increases in entropy are favorable when taken alone. Overall, to be thermodynamically favorable, a negative ∆G is required. This equation can be used to represent the three steps of dissolution described above, keeping the system isothermal.
Using Figure 3.3, step one of the dissolution scheme, breaking of the solute lattice to free a solute particle, can be represented with ∆H1 and ∆S1. This action increases enthalpy but decreases entropy (∆H ↑, ∆S ↓).
Step two, the opening of the solvent, can be represented with ∆H2 and ∆S2. This action increases enthalpy (∆H), while the change in entropy depends on whether or not the solvent molecules need to be ordered to allow the solute molecule in (∆H ↑, ∆S ↑↓).
Step three, the insertion of solute into the solvent, can be represented with ∆H3 and ∆S3. This action increases enthalpy but decreases entropy (∆H ↑, ∆S ↓).
Overall, the process involves enthalpy (H) changes of ∆H1, ∆H2 and ∆H3. It also involves entropy (S) changes of ∆S1, ∆S2 and ∆S3. Thermodynamically, we are interested in the total, final change only. For the three-step process, the free energy of solution is: ∆Gsoln = (∆H1 + ∆H2 + ∆H3) – T(∆S1 + ∆S2 + ∆S3). As stated above, in order for a solute to dissolve, the overall ∆G must be negative. This obviously is the case when Σ∆H is less than Σ∆S (Σ∆H < Σ∆S), regardless of the individual values.
Another way of looking at this three-step process is simply considering the sum of work done to accomplish each of the steps. If solvent molecules are labeled as ‘1’, and solute molecules as ‘2’, the simple ‘work equations’ are: 1) step one gains PE and the work done = w22 (work of two solute molecules); the work in step two = w11; the increase in PE, or work, is –w12 for closing the hole, and an additional –w12 for net work in the final step. Therefore, the overall work = w22 + w11 – 2w12. Using either approach, the three-step dissolution process must be thermodynamically favorable in order for it to occur. That said, even a thermodynamically favorable change only can occur – there is no certainty it will occur.
IV. Temperature
Temperature affects solubility and is also thermodynamically related. The effect of temperature on solubility depends whether the particular dissolution process is endothermic or exothermic in nature and the ambient environmental conditions. Endothermic processes are reactions in which heat is absorbed (ΔH > 0). Exothermic processes are those in which heat is released (ΔH < 0). If the ambient temperature is relatively high, exothermic dissolution processes will be inhibited, while endothermic dissolution processes will be improved. So, high ambient temperatures will increase the solubility of solutes with endothermic dissolution processes, but decrease the solubility of those with exothermic processes.
V. Ionization of solute and solvent, and pH of the solvent
It is assumed the reader is familiar with the Henderson–Hasselbalch equation, pH = pKa + log ([A−]/[HA]), where [A−] = molar concentration of a conjugate base (ionized form), and [HA] = molar concentration of an undissociated (unionized) weak acid. The pH of the solvent can greatly impact the solubility of ionizable solutes. Acidic drugs are less soluble in acid solutions because more of the drug tends to be in the unionized form, which is less able to interact with the solvent (water) than the ionized form. The dependence of the solubility of an acidic drug on ionization of the drug, in acidic conditions, is represented by equation A:
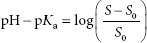
where S is the solubility of the of the ionized drug and S0 is the solubility of the unionized drug.
The solubility of basic drugs in relation to pH is represented by equation B:
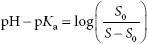
where S is the solubility of the of the unionized drug and S0 is the solubility of the ionized drug.
The zwitterion form has the lowest solubility, S0. At pH values below the isoelectric point (pKa), equation B is used. For pH values above the isoelectric point, equation A is used.
The previous discussion tells us why there are specific solubility limits, but not why there are different dissolution rates.
What is dissolution, exactly? In simple terms it is the process of a solute dispersing/dissociating in a solvent, forming a molecular-level, chemically and physically homogenous dispersion, called a solution. In contrast to solubility, when we speak of dissolution, it is understood that rate is a major consideration. Solubility is an endpoint. Dissolution is a process. There are different types of solutions of course. Examples of solutions, with all phase combinations, are shown in Table 3.1.
For this text, discussion is focused on liquid-in-liquid and solid-in-liquid solutions – and so the solubility and dissolution for such solutions. Within ‘solid-in-liquid solutions,’ there are two major types of dissolution. In the first type, the solution’s phase contains the same solute chemical entity as is found in the original solid phase. Upon removal of solvent, the solute can be recovered unaltered by the dissolution process. An example is the dissolution of sucrose in water (Figure 3.4).



