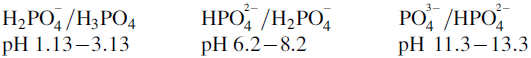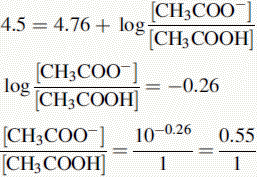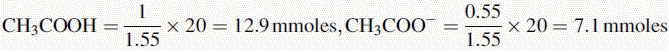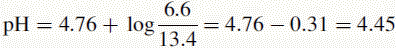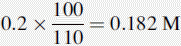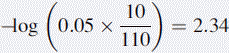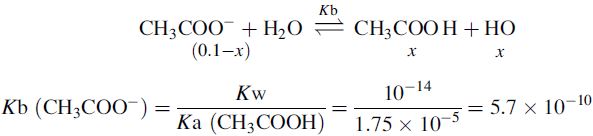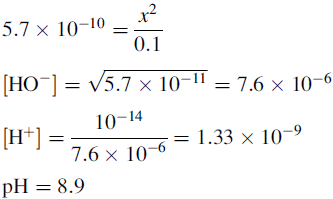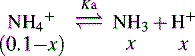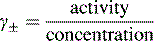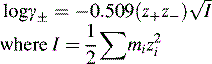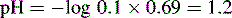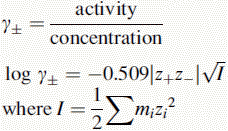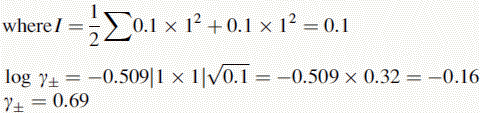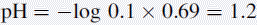2 Physical and chemical properties of drug molecules
Introduction
The physical properties of organic molecules, such as pKa and partition coefficient, are dealt with extensively in pharmacy courses1,2 but do not feature greatly in analytical chemistry courses. It is often surprising that analytical chemists cannot distinguish between, for instance, basic, weakly basic, acidic, weakly acidic and neutral nitrogen functions. The physical properties of drug molecules, along with simple chemical derivatisation and degradation reactions, play an important part in the design of analytical methods. Drug molecules can be complex, containing multiple functional groups that in combination produce the overall properties of the molecule. This chapter will serve as a starting point for understanding the chemical and physico-chemical behaviour of drug molecules, which influence the development of analytical methods. The latter part of the chapter focuses on some typical drugs that are representative of a class of drug molecules and lists their physical properties and the properties of their functional groups in so far as they are known.
Calculation of pH value of aqueous solutions of strong and weak acids and bases
Dissociation of water
In pure water the concentration of hydrogen ions is governed by the equilibrium:
Acidic and basic strength and pKa
The pKa value of a compound is defined as: pKa = − log Ka.
A pKa value can be assigned to both acids and bases.
For an acid, the higher the [H+] the stronger the acid, e.g.:
In the case of a base, it is the protonated form of the base that acts as a proton donor, e.g.:
In this case, the lower the [H+] the stronger the base.
Henderson–Hasselbalch equation
Can be rearranged substituting pH for −log [H+] and pKa for −log Ka to give:
Thus, when the pH = 4.76, then:
For a base, the Henderson–Hasselbalch equation is written as follows:
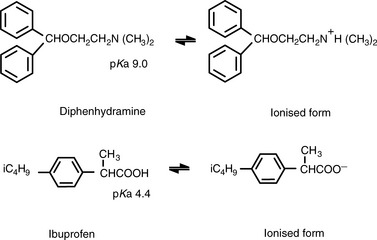
Ionisation of drug molecules
Buffers
Using the Henderson–Hasselbalch equation:
The buffer is composed of 1 part acetic acid and 0.17 part acetate.
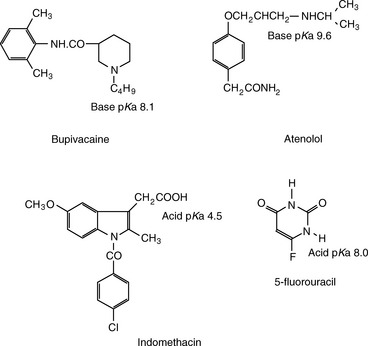
Determine the buffer range(s) for the following compounds:
Number of mmoles of acetate + acetic acid in 100 ml of buffer = 0.2 × 100 = 20 mmoles.
Using the Henderson–Hasselbalch equation:
The buffer contains 1 part CH3COOH and 0.55 parts CH3COO−.
When HCl is added the following reaction occurs:
The amount of HCl added is 10 × 0.05 = 0.5 mmoles
Therefore, after addition of HCl, the amount of acetate remaining is:
The amount of acetic acid now present is:
The new pH of the buffer is 4.45.
If 10 ml of 0.05 M HCl were added to 100 ml of water, the pH would be determined as follows:
Activity, ionic strength and dielectric constant
z is the charge on a particular ion.
I is the ionic strength of the solution.
m is the molality (moles per kg of solvent) of a particular ion in solution.
For dilute solutions the molality can be approximated to the molarity
Using this equation, the activity of H+ in 0.1 M HCl can be calculated:
Thus, the true pH of 0.1 M HCl is calculated as follows:
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


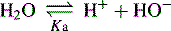
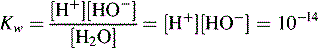
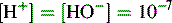
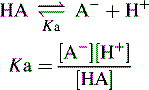
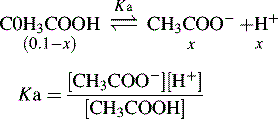
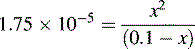
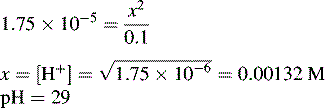
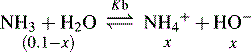
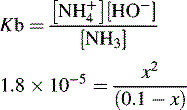
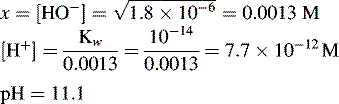
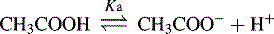
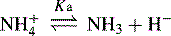
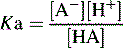
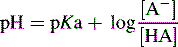
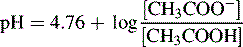
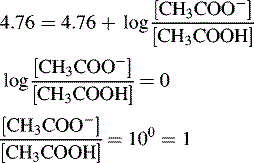
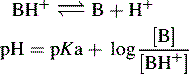
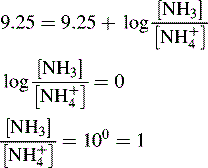
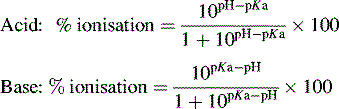
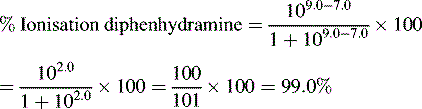
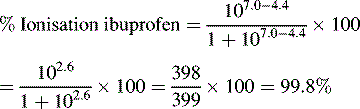
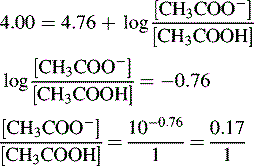
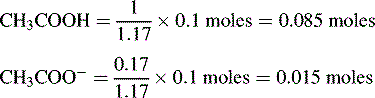
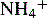 and NH3 in the buffer at pH 9.0 and indicate an alternative method for preparing the buffer.
and NH3 in the buffer at pH 9.0 and indicate an alternative method for preparing the buffer.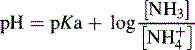
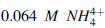 The buffer could be prepared by mixing 360 ml of a 0.1 M ammonia solution with 640 ml of 0.1 M NH4Cl
The buffer could be prepared by mixing 360 ml of a 0.1 M ammonia solution with 640 ml of 0.1 M NH4Cl