Chapter 2

Pharmacodynamics

2.1 General principles of drug action

Drugs act on many different targets and in diverse ways. Nevertheless, there are some general principles of drug action that are applicable to many drugs; these are the subject of pharmacodynamics. In this chapter, we are going to cover the following concepts:

• Theory of drug-receptor interaction
  
• The two-state model of receptor activation
  
• Dose-effect relationships and their modulation by signaling cascades
  
• Potency, efficacy and therapeutic index

2.1.1 The invention of the receptor concept

Notes: In this excerpt from his Nobel lecture [4], Paul Ehrlich develops the idea of receptor blockade. Although this concept is viable and important, it does not account for the effect of tetanus toxin. Instead, tetanus toxin is a protease that cleaves synaptobrevin, an intracellular protein that is important for neurotransmitter exocytosis (see slide 6.10.8).

The receptor concept is fundamental to pharmacology. As stated above, most receptors are protein molecules; in this chapter, we will confine the discussion to this case.

2.1.2 How do drugs affect their receptors?

• Mode of binding: Reversible vs irreversible
  
• Binding site: Orthosteric vs allosteric
  
• Functional effect: Activation vs inhibition

Notes: Most drugs bind their targets reversibly and non-covalently, but some important exceptions exist. Furthermore, binding is orthosteric in most cases, which means that the drug binds to the receptor within the same site as the receptor’s physiological ligand. For example, all of the antagonists of histamine and angiotensin that were discussed in slides 1.2.3–1.2.8 bind orthosterically.

Orthosteric binding implies that the receptor can not bind its physiological ligand and the drug at the same time; if both are present, they will compete for binding to the receptor.

A drugs that activates its receptor is referred to as an agonist, whereas an inhibitory drug is also called an antagonist. Drugs that target enzymes are virtually always antagonists, while with hormone and neurotransmitter receptors there usually are both agonistic and antagonistic drugs. Where this is the case, only one or the other may have therapeutic value; for example, with histamine receptors, only antagonists are clinically useful.

2.1.3 Labetalol as an example of stereoselective drug action

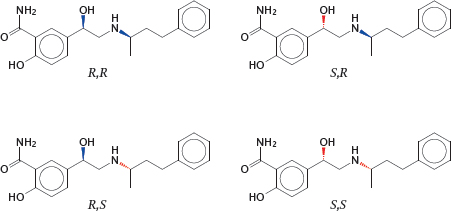
Notes: As with enzymes and substrates, the mutual selectivity of receptors and drugs is based to a great extent on the “lock and key” principle, that is, on steric complementarity. Like enzyme substrates, many drug molecules are chiral, which means that they occur as R and S (or L and D) enantiomers. Since proteins consist of L-amino acids only, they are also chiral molecules. Therefore, we should expect protein receptors to interact with drugs in an enantioselective manner. This is indeed the case; a good example of this is the drug labetalol.

Labetalol, an α- and β–adrenergic receptor antagonist, is a racemic mixture of four stereoisomers. The R,R isomer carries most of the β-adrenergic blocking activity, whereas the S,R isomer carries most of the α-blocking activity. The R,S and S,S isomers are dead freight.

Many drugs occur as racemic mixtures, and as with labetalol the isomers will often differ in specificity and activity. Ideally, one would purify the isomer that has useful pharmacological activity, and remove others that are inactive and might only contribute to toxicity. However, in practice, this purification can be difficult and costly, and it is usually done only where necessary to avoid significant drug toxicity.

2.1.4 Two natural stereoisomers with separate therapeutic uses

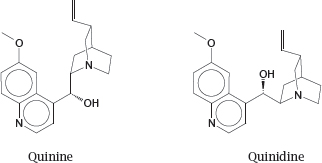
Notes: Both quinine and quinidine are obtained from the bark of the Cinchona tree. Quinine is used against malaria; its mechanism of action is believed to resemble that of chloroquine (slide 11.9.1).

Quinidine also has some antimalarial activity, but is used in clinical medicine for its inhibitory effect on sodium channels in the heart, which is useful in certain types of cardiac arrhythmias.

2.2 Theory of drug-receptor interaction

Both in its assumptions and its conclusions, the theory of drug-receptor interaction is quite similar to enzyme kinetics, and it might be a good idea to dust off your biochemistry textbook to refresh your memory on that subject.

2.2.1 Mass-action kinetics of drug-receptor binding

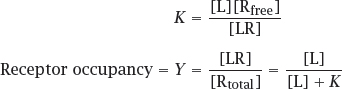
Notes: The law of mass action represents the simplest possible case, but nevertheless an experimentally important one. The key parameter here is the receptor occupancy, that is, the fraction of receptor that is bound to the ligand and therefore subject to the ligand’s functional effect. The second equation assumes that the ligand is present in excess over the receptor, which is almost always the case.

2.2.2 Linear and semilogarithmic plots of receptor occupancy

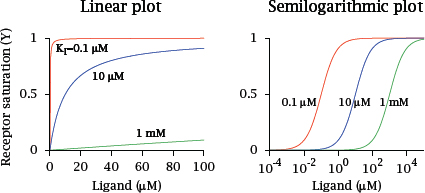
Notes: Receptor saturation, as a function of ligand concentration, can be plotted in various formats. The linear plot shows that, at ligand concentrations well below the dissociation constant, receptor saturation increases in an approximately linear fashion. At concentrations significantly greater than the dissociation constant, it approaches saturation and changes very little.

An advantage of the linear plot is freedom from distortion. However, it is not good at covering a wide range of ligand concentrations or affinities. For this purpose, a semilogarithmic plot—with a logarithmic scale for the ligand concentration—is more convenient. We will mostly use this plot format in the following.

2.2.3 The Scatchard plot

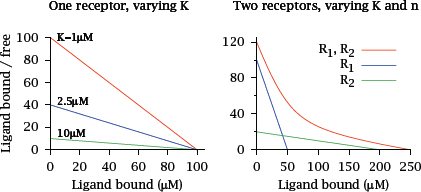
Notes: The Scatchard plot is another way to depict the binding of ligands to receptors. In order to construct this plot, the concentrations of both receptor-bound ligand and free ligand are measured, and the ratio of bound to free ligand is plotted against the concentration of free ligand.

It is easy to show that, if all drug molecules bind to a single class of receptors with uniform affinity, all data points will fall on a straight line. Therefore, if the plotted line is not straight, this suggests that the binding sites are inhomogeneous and vary in affinity. Note, however, that this requires ligand binding to follow simple mass action kinetics, which is not always the case (see slide 2.5.1).

Also note that the Scatchard analysis does not assume that the concentration of the ligand always exceeds that of the receptor—in fact, some of the data points in the curve must be obtained at limiting ligand concentrations; otherwise, the γ coordinate would be very low for all data points. This is usually accomplished by the use of radioactively labeled drug molecules, which can be measured accurately at such low concentrations.

2.3 Reversible and covalent receptor inhibition

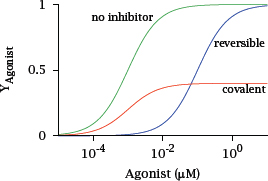
Notes: As pointed out above, most drugs bind their targets orthosterically, that is, they dislodge some physiological agonist—such as histamine or angiotensin—from its receptor. If the drugs do not themselves activate the receptor, this will cause inhibition.

The drugs may bind either noncovalently and reversibly, or covalently and irreversibly.¹ It turns out that the two cases affect the receptor quite differently: With a reversible inhibitor, the dose-response curve for the physiological agonist is shifted to the right, while with a covalent inhibitor it is vertically compressed.

2.3.1 Theory of competitive inhibition

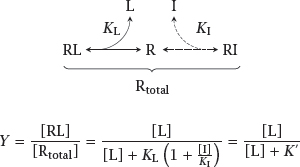
Notes: Competitive inhibition occurs when a physiological agonist and an inhibitory drug bind reversibly to the same binding site on their receptor. The two binding equilibria are linked by the free receptor, which can only engage in one reaction at any time.

Let K_L and K_I be the dissociation constants that govern binding of the physiological agonist and the inhibitor, respectively. Then, if the concentration of the inhibitor [I] is fixed, we can comprise the entire term K_L(1 + ^[I]/K_I) into a single number, K′. Since K′ is necessarily greater than K_L, the resulting curve in the semilogarithmic plot is shifted to the right relative to the situation without inhibitor, as illustrated in slide 2.3.

Try to derive this equation on a rainy day—it’s all basic high school math. You’ll be glad you did!²

2.3.2 Theory of irreversible or covalent inhibition