Pharmaceutical calculations

19


Pharmaceutical calculations




Study Points



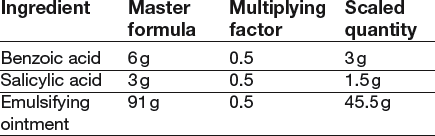
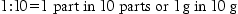image Expressions of concentration


image Calculating quantities from master formulae


image Changing concentrations


image Small quantities (trituration)


image Solubility


image Calculations related to doses


image Reconstitution and rates of infusion



Introduction


Most pharmaceutical calculations are simple arithmetic. Calculating quantities in the dispensing process requires careful, methodical working which will minimize the risk of errors. Always try to relate the calculation to practice, visualize what you are doing and double-check everything.



How to minimize errors


As in all dispensing procedures, an organized, methodical approach is essential:



image Write out the calculation clearly – it is all too easy to end up reading from the wrong line


image If you are transferring data from a reference source, double-check what you have written down is correct


image Write down every step


image Do not take short cuts – you are more likely to make a mistake


image Try not to be totally dependent on your calculator – have an approximate idea of what the answer should be and then if you happen to hit the wrong button on the calculator you are more likely to be aware that an error has been made


image Finally, always double-check your calculation. There is frequently more than one way of doing a calculation, so if you get the same answer by two different methods the chances are that your answer will be correct. Alternatively, try working it in reverse and see if you get the starting numbers



Expressions of concentration


The metric system is the International System of Units (SI Units) for weight, volume and length. The basic unit for weight is the kilogram (kg), the basic unit for volume is the litre (L) and the basic unit of length is the metre (m). The prefix ‘milli’ indicates one-thousandth (10−3) and ‘micro’ one-millionth (10−6).


In some countries, the avoirdupois (or imperial) system (pounds and ounces) is still used in commerce and daily life. The imperial system of volume (pints and gallons) is still a common system for commerce and household measurement. Pharmacists need to know about these systems in order to avoid serious errors in interpretation of prescriptions. It is important to be able to change between the systems. Some conversion factors for the metric and avoirdupois systems are shown in Box 19.1 (see Examples 19.1–19.3).



Box 19.1   Weights and measures





Example 19.1


A prescription is received for a dose of 125 mg of a drug. How many grams is the dose?


1 g = 1000 mg. Therefore:




Example 19.2


A 1-year-old child weighs 9 kg. What would this be in pounds (lb)?


1 kg = 2.2 lb. Therefore:




Example 19.3


Gentamicin eye drops contain 200 drops in a 10 mL bottle. Calculate the volume of 1 drop.


200 drops = 10 mL. Therefore:




Expressions of strength


Ratio is the relative magnitude of two like quantities. Thus:


image


If 1 g of sucrose is in 10 g of solution, the ratio is 1:10. Therefore, 10 g of sucrose is in 100 g of solution. This can be expressed as a percentage, so it is equivalent to a 10% w/w (weight in weight) solution.


Ratio strength is the expression of a concentration by means of a ratio, e.g. 1:10. Percentage strength is a ratio of parts per hundred, e.g. 10% (see Examples 19.4–19.6).



Example 19.4


Express 0.1% w/w as a ratio strength:



Therefore, the ratio strength = 1:1000



Example 19.5


Express 1:2500 as a percentage strength:



Thus, y = 1 × 100/2500 = 0.04%



Example 19.6


Express 1 p.p.m. as a percentage strength:



Let y be the percentage strength:


Thus, 1 part/1 000 000 = y parts/100 parts







Miscellaneous examples


See Examples 19.10–19.13.



Example 19.10


Express 30 g of dextrose in 600 mL of solution as a percentage, indicating w/w, w/v or v/v.


Let y grams be the weight of dextrose in 100 mL:




Example 19.11


What is the percentage of magnesium carbonate in the following syrup? Percentage is the number of grams of magnesium carbonate in 100 mL of syrup.













Magnesium carbonate 15 g
Sucrose 820 g
Water, q.s. to 1000 mL



Example 19.12


Calculate the amount of drug in 5 mL of cough syrup if 100 mL contains 300 mg of drug.


By proportion,




Example 19.13


Compute the percentage of the ingredients in the following ointment (to 2 decimal places):













Liquid paraffin 14 g
Soft paraffin 38 g
Hard paraffin 12 g

Total amount of ingredients



To find the amounts of the ingredients in 100 g of ointment, each figure will be multiplied by 100/64:



It is useful to double-check that these numbers add up to 100% (allowing for the rounding off to 2 decimal places).



Moles and molarity


Concentrations can also be expressed in moles or millimoles (see Ch. 41). When a mixture contains the molecular weight of a drug in grams in 1 litre of solution, the concentration is defined as a 1 molar solution (1 mol). It has a molarity of 1. Thus, for example, the molecular weight of potassium hydroxide (KOH) is the sum of the atomic weights of its elements, i.e. KOH = 39 + 16 + 1 = 56. Therefore a 1 molar solution (1 mol) of KOH contains 56 g of KOH in 1 litre of solution.


A 1 millimole (mmol) solution of KOH contains one-thousandth of a mole in 1 litre = 56 mg (see Examples 19.14–19.16).



Example 19.14


Calculate the number of moles (molarity) of a solution if it contains 117 g of sodium chloride (NaCl) in 1 L of solution (atomic weights: Na = 23, Cl = 35.5):



Therefore, 58.5 g of NaCl in 1 litre is equivalent to 1 mole (1 mol) in solution.


Number of moles of NaCl = 117 g/58.5 g = 2 mol



Example 19.15


Calculate the number of milligrams of sodium hydroxide (NaOH) to be dissolved in 1 L of water to give a concentration of 10 mmol (atomic weights: H = 1, O = 16, Na = 23):



1 mmol = 40 mg in 1 L


Therefore, 10 mmol = 400 mg in 1 L



Example 19.16


Express 111 mg of calcium chloride (CaCl2) in 1 L of solution as millimoles (atomic weights: Ca = 40, Cl = 35.5):



Therefore, 111 mg of CaCl2 = 1 mmol in 1 L



Calculating quantities from a master formula


In extemporaneous dispensing, a list of the ingredients is provided on the prescription or is obtained from a reference source. It may be that this ‘formula’ is for the quantity requested, but more often, the quantities provided by the master formula have to be scaled up or down, depending on the quantity of the product required. This can be achieved using proportion or by deriving a ‘multiplying factor’. The latter is the ratio of the required quantity divided by the formula quantity. The following examples illustrate this process (Examples 19.17 and 19.18).



Example 19.17


Calculate the quantities to prepare the following prescription:


50 g Compound Benzoic Acid Ointment BPC.


The master formula is for 100 g, the prescription is for 50 g, therefore the multiplying factor is 50/100, i.e. each quantity in the master formula is multiplied by 50/100 = 0.5 to give the scaled quantity.



image


Double-check: the quantities for the master formula add up to 100 g and the scaled quantities add up to 50 g.



Example 19.18


You are requested to dispense 200 mL of Ammonium Chloride Mixture BPC. The formula can be found in a variety of reference books such as Martindale. In this example, the master formula gives quantities sufficient for 10 mL. As the prescription is for 200 mL, the multiplying factor is 200/10. Thus the quantity of each ingredient in the master formula has to be multiplied by 20 to provide the required amount.
























Ingredient Master formula Scaled quantity
Ammonium chloride 1 g 20 g
Aromatic solution of ammonia 0.5 mL 10 mL
Liquorice liquid extract 1 mL 20 mL
Water to 10 mL to 200 mL

Because this formula contains a mixture of volumes and weights it is not possible to calculate the exact quantity of water which is required. However, it is always good practice to have an idea of what the approximate quantity will be. The liquid ingredients of the preparation, other than the water, add up to 30 mL and there is 20 g of ammonium chloride. The volume of water required will therefore be between 150 mL and 170 mL.


In most formulae where a combination of weights and volumes is required, the formula will indicate that the preparation is to be made up to the required weight or volume with the designated vehicle. However, occasionally, as can be seen in the next example, a combination of stated weights and volumes is used and it is not possible to indicate what the exact final weight or volume of the preparation will be. In these instances an excess quantity is normally calculated for and the required amount measured (Example 19.19)



Example 19.19


Calculate the quantities required to produce 300 mL Turpentine Liniment BP 1988.



















Ingredient Master formula
Soft soap 75 g
Camphor 50 g
Turpentine oil 650 mL
Water 225 mL
< div class='tao-gold-member'>

Related posts:

  1. Oral unit dosage forms
  2. Solutions
  3. Public health
  4. Emulsions

Stay updated, free articles. Join our Telegram channel
Tags:
Jun 24, 2016 | Posted by in PHARMACY | Comments Off on Pharmaceutical calculations

Full access? Get Clinical Tree
Get Clinical Tree app for offline access