Chapter 2 This chapter describes the three fundamental types of measurements used in observational studies and how data based on each type are summarised and introduces the concepts of risk and risk factors and how evidence for a causal link between an exposure and outcome measure could be determined. All observational studies involve collecting data from or about participants. The data may include many factors (or variables), such as demographic information, data about current or past lifestyle and habits, physical or psychological symptoms, or biochemical or imaging markers. To make sense of a dataset and to communicate the findings, it is essential to summarise the data in a quantitative and objective way [1–3]. For example, a study conclusion that ‘smoking is very bad for you’ is easy to read, but provides no useful information. The word ‘very’ is highly subjective. What does ‘bad for you’ mean? Is it an increased risk of the following: To describe a set of characteristics among a group of people, or examine relationships between exposures and outcomes, requires four key stages: Summarising data is achieved by classifying the type of measurement into one of three possible categories, after first determining the unit of interest. In observational studies this is almost always a single individual (person).1 Consideration is then given to the way in which the unit of interest (i.e. person) will be evaluated when measuring the endpoint or factor. The three categories are: Box 2.1 defines these groups, and shows examples. Knowing into which of the three categories the outcome measure of interest falls is essential for: In a study of the effect of an exposure on an outcome, the exposure is usually categorised as ‘counting people’ or ‘taking measurements on people’; it is unusual (statistically difficult) to have an exposure that involves time-to-event data, unless they have all had the event, in which case the measure can be treated as a continuous factor. There are established statistical methods for analysing each type of outcome measure. The more simple methods can examine the effect of only one exposure on one outcome measure, each measured only once, but more powerful methods (regression analyses) can allow examination of several exposures, or one exposure and several confounding factors (see Chapter 4). Sections 2.2 to 2.4 introduce the three categories of outcome measures when considering a single group of people, and researchers should always consider how to display data in a diagram. Further details of how some of the statistics are calculated are found elsewhere [1-3]; the focus here is on interpretation. To investigate associations, comparisons are made between two or more groups, covered in Chapter 3. This type of outcome measure is easily summarised by calculating the percentage or proportion. For example, the prevalence of smokers among a group of individuals is found by counting how many people smoke, and dividing this number by the total number of individuals. When examining disorders, the proportion can be called risk, and the simplest calculation is the number of individuals with the disorder divided by the total number in the group. Risk and risk factors are described in more detail in Section 2.6. ‘Counting people’ endpoints can be shown diagrammatically using a bar chart (e.g. Figures 5.1 and 5.2). Whereas data based on ‘counting people’ endpoints can be summarised by a single parameter (proportion), taking measurements on people requires two parameters: typical value and spread (some measure of how much the outcome varies between people). The following cholesterol levels (mmol/L) for 40 healthy men are ranked in order of size: A typical value, the ‘average’ or measure of central tendency, is where the middle of the distribution lies. Two measures are: Some men will have a cholesterol value below 6.4, some above, and some exactly 6.4, but the average is 6.4 mmol/L. The mean or median cannot describe the whole range of values. Therefore using a single summary number to help interpret the data will be imperfect, but makes it easier to interpret the data. Two measures of spread are: ‘Taking measurements on people’ endpoints can be shown diagrammatically using scatter plots (see Figure 4.1, and also Figure 5.3). Deciding which measures of average and spread to use depends on whether or not the distribution is symmetric. To determine this, the data can be grouped into categories of cholesterol levels, to produce a frequency distribution, and the percentage (proportion) in each group are used to create a histogram (the shaded boxes in Figure 2.1). The shape is reasonably symmetric, indicating that the distribution is Gaussian or Normal2, which is more easily visualised by drawing a bell-shaped curve (Figure 2.1). Figure 2.1 Histogram of the cholesterol values in 40 men, with a superimposed Normal (Gaussian) distribution curve. When data are Normally distributed, the mean and median are similar, and the preferred measures of average and spread are the mean and standard deviation, because they have useful mathematical properties which underlie many statistical methods used to analyse this type of data. When the data are not Normally distributed, the median and interquartile range are better measures. Distributions can be positively skewed or skewed to the right, where the tail of the data is (i.e. the values are ‘bunched’ up towards the lower end of the range); or negatively skewed, when the tail of the data is towards the left. The mean and median will be very different, but the median is usually a better measure of a typical value. When data are skewed, transformations may make the distribution approximately Normal (symmetric): logarithms, square root or reciprocal (positive skew), or square or cubic (negatively skew). Many biological measurements only have a Normal distribution after the logarithm is taken. The mean is calculated on the log of the values, and the result is back-transformed to the original scale, though this cannot be done with standard deviation. Negative skewed data could also be ‘reflected’: subtract them all from the largest value then add one (making the distribution positively skewed), and then apply logarithms. Sometimes there is no transformation that will turn a skewed distribution into a reasonably Normal one. A reliable approach for assessing Normality is examining a probability (or centile) plot3, which statistical software packages can easily provide. There are various versions, but the only aspect that matters is that the observations lie reasonably along a straight line, if the data are approximately Normally distributed (some curvature, or a few outliers at either end are often acceptable). As with ‘counting people’ endpoints, an ‘event’ needs to be defined for time-to-event data. The simplest and most commonly used is ‘death’, hence the term survival analysis. In the following seven participants, the endpoint is “time from baseline until death, in years”, and all seven participants have died: The mean (7.7 years) and median (8.3 years) are easily calculated (as with ‘taking measurements on people’). However, in another group of nine participants, not all have died at the time of statistical analysis: Here, the mean or median cannot be calculated in the usual way, until all the participants have died, which could take many years. Calculating the average time until death by ignoring those who are still alive is incorrect; the summary measure would be biased downwards because insufficient time has elapsed for the others to die, after which the average time to death would be longer. Alternatively, we could obtain the survival rate at a designated point. Among the 9 people, two died before 3 years and 7 lived beyond, so the 3-year survival rate is 7/9 = 78%. This is then simply an example of ‘counting people’. Every participant would need to be followed up for at least 3 years, unless they died, and the outcome (dead or alive) must be known at that point for all participants. There are two main problems: (i) losing contact with some participants, particularly after long follow up, and (ii) this approach does not distinguish between someone who died at 2 months from another person who died at 2.5 years. A better approach is to use a life-table, which produces a Kaplan-Meier curve. In the example above, the ‘time from baseline until death or last known to be alive’ is one variable, and another variable has values 0 or 1 to indicate ‘still alive’ or ‘dead’. Someone who is still alive (i.e. not had the event of interest), or last known to be alive at a certain date, is said to be censored. This approach uses the last available information on every participant, and allows for how long he/she has lived, or has been in the study. Table 2.1 is the life table for the group of nine participants above, and the first and last columns are plotted to produce the Kaplan-Meier curve in Figure 2.2. When each participant dies, the step drops down. The four censored participants contribute no further information to the analysis after the date when they were last known to be alive. It is possible to estimate two summary measures from Figure 2.2 or Table 2.1: median survival, and a survival rate at a specific time point. Median survival is reliable when many events have occurred, fairly continuously, throughout the study; otherwise it can be skewed by only one or two events. Sometimes, an event (survival) rate at a specific time point is preferred. Figure 2.2 Kaplan–Meier plot of the survival data for the nine participants on page 30, which can also be used to estimate survival rates and median survival: 4-year survival rate: A vertical line is drawn on the x-axis at 4, and the rate is the corresponding y-axis value where the line hits the curve, that is, 78%.Median survival: The time at which half the participants have died. A horizontal line is drawn on the y-axis at 50%, and the corresponding x-axis value (median) is where the line hits the curve, that is, 7.2 years. When all participants have had the event of interest (such as death), the Kaplan-Meier median survival will be the same as the simple median from a ranked list of numbers. The two medians are only different when some participants are censored (i.e. not had the event). The median is used instead of the mean, because time-to-event data often has a skewed distribution. The usual Kaplan-Meier plot has a vertical (y) axis which represents the event-free rate (e.g. survival), so the curve starts at 100% at time zero. This is useful when events (here deaths) tend to occur early in the study. However, the plot could instead have a vertical axis that represents the event rate, so the curve starts at 0% at time zero (i.e. it uses 100 minus the fourth column in Table 2.2). This type of plot may be more informative when events tend to occur later on. A curve based on the event-free rate must start at 100% at time zero, but because the y-axis for a plot showing the event rate starts at zero, the upper limit can be less than 100%. In the section above, the ‘event’ in the time-to-event endpoint is ‘death’, sometimes called overall survival (OS), because it relates to death from any cause. It is simple because it only requires the date of death. The methods can apply to any endpoint that involves measuring the time until a specified event has occurred, for example, time from entry to a study until the occurrence or recurrence of a disorder or any change in health status, such as time until hospital discharge. Two other common measures associated with the risk of a disorder are: When considering OS, DFS or EFS, the terminology implies that interest is in those who survive (i.e. do not have the event of interest). However, the analysis and interpretation focus on the event itself (mortality or the event/disorder). The traditional approach in medical research studies is to consider the concept of a true effect. For a single group of individuals, this could be a true proportion, mean value, median survival time, or event rate at a specific time point. As an example, in a cross-sectional study of UK vocational dental practitioners (VDP) (see Box 5.2 and Table 5.1), there was a finite number (n = 767) of individuals in the population in 2005, and one aim was to examine their alcohol habits. If every single VDP responded to the survey, and did so truthfully, this would give the true prevalence of alcohol use without uncertainty. However, of the 767 registered VDPs, 502 responded, so there will be uncertainty over the habits among the 265 who did not. Table 2.1 Life table for the survival data of nine participants on page 30. * The chance of being alive at a certain time point, given that the person has survived up to that point; calculated using a formula [1]. To obtain the 4-year survival rate from the table, it is necessary to ascertain whether there is a value at exactly 4 years. Because there is none, the closest value from below is taken, that is, at 3.3 years: 4-year survival rate is 78%. To obtain the median survival, the point at which 50% of study participants are alive is determined. The closest value from below is 43%, so the median is 7.2 years. The original study research question is fundamental. In the VDP study, this was ‘What is the prevalence of smoking, alcohol, and recreational drug use among all UK VDPs in 2005?’. The word all is key. Because the study aimed to observe all UK VDPs, inferences about the 767 have to be made, based on data from the 502 study participants. In most situations, it is not possible to know the size of the target population, nor is it feasible to evaluate them all. For example, finding the prevalence of adult smokers in the UK would require many millions of adults to complete a survey; and knowing the risk of developing heart disease among females in the US would require a study of every female who ever lived there and knowing her heart disease status. The study population therefore usually represents only a very small proportion of the target population, even though the latter is of ultimate interest. In the VDP study, 207 out of 502 (41%) participants were classified as a binge drinker, as shown below: The best estimate of the true prevalence is 41%, but it would be inappropriate to say that the true value is exactly 41%. If there had been other studies, the observed prevalence could be 45%, 38%, and so on; all different due to natural variation (or chance) and the fact that there just happened to be a few more or a few less reported binge drinkers in each study. The observed prevalence (41%) and the sample size (N = 502) are used to produce a 95% confidence interval (CI), which essentially produces a range of values for the true prevalence:
Outcome measures, risk factors, and causality
2.1 Types of measurements (endpoints)
2.2 ‘Counting people’ (risk)
2.3 ‘Taking measurements on people’
3.6
3.8
3.9
4.1
4.2
4.5
4.5
4.8
5.1
5.3
5.4
5.4
5.6
5.8
5.9
6.0
6.1
6.1
6.2

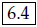
6.5
6.6
6.8
6.9
7.1
7.2
7.2
7.3
7.4
7.5
7.7
8.0
8.1
8.1
8.2
8.3
9.0
9.1
10.0
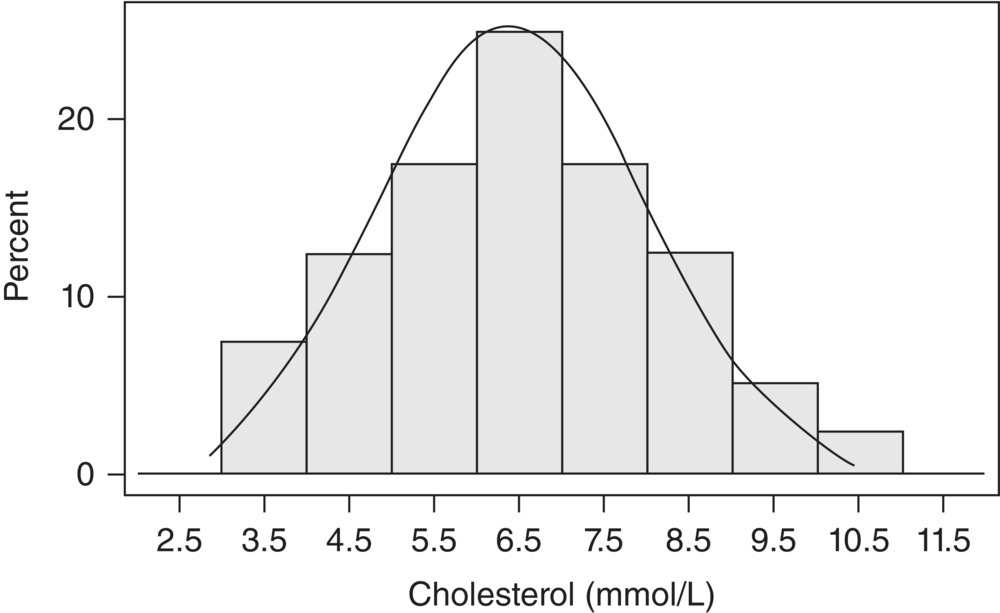
2.4 Time-to-event data
4.5
6.1
6.7
8.3
9.1
9.4
10.0
2.7
2.9
3.3
4.7
5.1
6.8
7.2
7.8
9.1
dead
dead
alive
dead
alive
alive
dead
dead
alive
Different types of time-to-event outcome measures
2.5 What could the true effect be, given that the study was conducted on a sample of people?
Time since diagnosis (years)
Censored (0 = yes, 1 = dead)
Number of participants at risk
Percentage alive (survival rate %)*
0
—
9
100
2.7
1
9
89
2.9
1
8
78
3.3
0
7
78
4.7
1
6
65
5.1
0
5
65
6.8
0
4
65
7.2
1
3
43
7.8
1
2
22
9.1
1
1
22
Prevalence of binge drinking
All UK VDPs (n = 767)
?? (true effect, i.e. true prevalence)
Study of 502 VDPs
41% (observed prevalence)
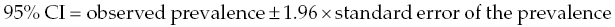
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


