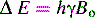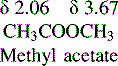8 Nuclear magnetic resonance spectroscopy
Applications in pharmaceutical analysis
• A powerful technique for the characterisation of the exact structure of raw materials, intermediates and finished products
• Can determine impurities, including enantiomeric impurities, without separation, down to ca the 10% level and 1% level with two-dimensional spectroscopy
• Can potentially be used for fingerprinting mixtures
• Has good potential for non-destructive quantitative analysis of drugs in formulations without prior separation.
Introduction
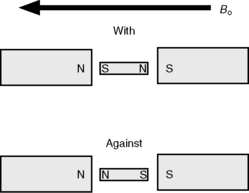
The spinning nuclei of certain atoms, 1H, 13C, 15N, 19F, 29Si and 31P, gives them the properties of a magnetic vector. When such nuclei are placed in a magnetic field they will tend to align with the field (Fig. 8.1). The energy difference between the spin being aligned with the field and against the field depends on the strength of the magnetic field applied. The greater the field strength the greater the energy difference Δ E:
where h is Planks constant; γ is the magnetogyric ratio of a particular nucleus; and Bo is the applied magnetic field.
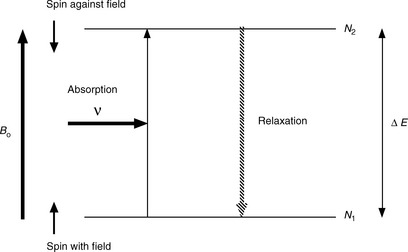
Figure 8.2 illustrates the absorption of energy to produce alignment against the applied magnetic field. Compared to other spectroscopic techniques, the energy difference between the ground and excited state is not large and thus Δ N, the difference between the number of protons in the low-energy (N1) and high-energy states (N2), is very small. This is because the energy difference between the two states is low relative to the thermal energy in the environment. This means that nuclear magnetic resonance (NMR) is a relatively insensitive technique because the net energy absorption by the population of low-energy protons in a sample is low. The wavelength of the radiation used in NMR is of low energy and is in the radiofrequency region. The units of energy used in NMR are in Hertz, which is a unit of frequency (c/λ, where c = 3 × 1010 cm/s and λ is in cm). The stronger the magnetic field applied, the greater the radiation frequency in Hertz (the shorter the wavelength) required to cause the spin of a nucleus to align against the field. The values for the strength of the applied magnetic field are in the range 14 000–140 000 Gauss (1.4–14 Tesla). A proton in the ground state will absorb radiation having a frequency of ca 60 MHz at 1.4 T and ca 600 MHz at 14 T. NMR instruments are described in terms of the frequency at which they cause protons to resonate; thus a 600 MHz instrument is one which causes protons to resonate at a frequency of ca 600 MHz. At higher magnetic field strength, greater sensitivity is obtained because of the greater difference in the populations of the higher and lower energy states. For a 60 MHz instrument the population difference between the ground and excited state for a proton is ca 1 in 100 000, whereas for a 600 MHz instrument the population difference is ca 1 in 10 000, i.e. about a 10-fold increase in sensitivity.
Instrumentation
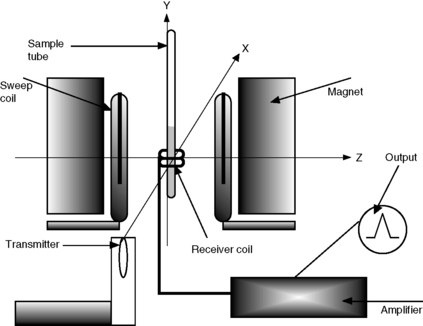
Figure 8.3 gives the basic layout of a continuous wave NMR spectrometer, which has largely been replaced by Fourier transform instruments. However, the principles of operation are broadly similar:
(i) The sample is placed in 3, 5, 10 millimetre glass NMR tubes and is spun in the fixed magnetic field in cases of one-dimensional experiments at ca 30 revolutions/s by means of an air turbine, thus ensuring uniformity of the magnetic field across the sample in a horizontal direction. The sample is analysed in solution in a deuterated solvent to ensure there is no interference with the signal from protons in the relatively much larger amount of solvent.
(ii) The reference point in parts per million (ppm) is determined by the resonance of the residual protons of the solvent which are used to lock the protons in a spectrum, e.g. the residual proton in deuterated chloroform is at 7.25 ppm.
(iii) In order to obtain a proton spectrum, the radiofrequency radiation is swept across a range of ca 10 ppm, e.g. 1000 Hz when the magnetic field is recorded on a 100 MHz instrument or 6000 Hz when the spectrum is recorded on a 600 MHz instrument. The receiver coil measures the absorption of radiation as the frequency is swept over the range being examined.
(iv) As well as determining the frequency at which protons in the molecule absorb, that is recorded as chemical shifts in ppm, the area of each signal proportional to the number of protons absorbing radiation is documented in integrals.
(v) Modern instruments, rather than being based on a continuous wave, are based on a pulsed wave. In brief, the short powerful pulse used in this type of spectroscopy behaves as a spread of frequencies covering the Hz range of interest, e.g. the range in which protons resonate. Most of the principles of the continuous wave instrument still hold but, rather than the absorption of radiation by the sample being observed, emission is observed as the excited protons relax back to their ground state following the short high-energy pulse of radiation. Thus spectra are accumulated using a high-intensity pulse followed by a time delay of a few seconds while the relaxation data of different protons in the molecule are collected. This type of procedure enables a spectrum to be acquired every few seconds, as opposed to a few minutes required to collect the data using a frequency sweep on a continuous wave instrument. The data from a number of pulses are accumulated using a computer, undergo mathematical manipulation known as Fourier transformation and are combined to produce a spectrum in which the signal to noise characteristics are much improved compared to a spectrum obtained on a single-scan continuous wave instrument.
Proton (1H) NMR
Chemical shifts
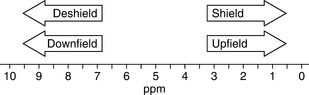
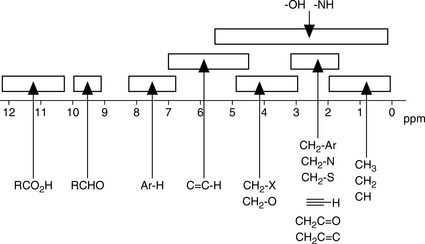
Proton (1H) NMR is the most commonly used form of NMR because of its sensitivity and the large amount of structural information it yields. The chemical shift is the position on the δ (delta) scale (in ppm) where the peak occurs (Fig. 8.4).
There are three major factors that influence chemical shifts:
1. Inductive effects by electronegative groups
2. Deshielding due to reduced electron density (due to the presence of electronegative atoms)
3. Anisotrophy (due to magnetic fields generated by π bonds).
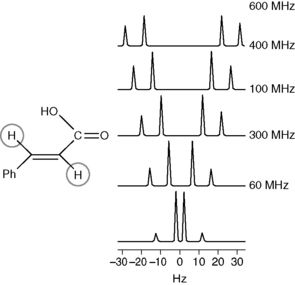
The exact absorption or resonance frequency of a proton depends on its environment. For example, a proton attached to carbon atom is affected predominantly by the groups which are separated from the carbon atom to which it is attached by one bond or, to a lesser extent, two bonds. As discussed earlier, the chemical shift of a proton is determined in relation to the residual protons of the deuterated solvent. Shift values for individual protons in a molecule are expressed in ppm and the frequency value of 1 ppm in Hertz depends on the strength of the applied magnetic field, which determines the energy required to excite a proton. For example, at field strength of 100 MHz a shift of 1 ppm has a frequency value of 100 Hz. Proton shifts in organic compounds range from slightly below 0 to 14 ppm, i.e. from a δ value of slightly less than 0 to a δ value of 14. The frequency difference between the shifts of the protons in Hz proportionally increases with the field strengths of the magnetic field corresponding to Larmor proton frequencies of ωo = 60, 100, 300 and 600 MHz, as exemplified in Figure 8.5.
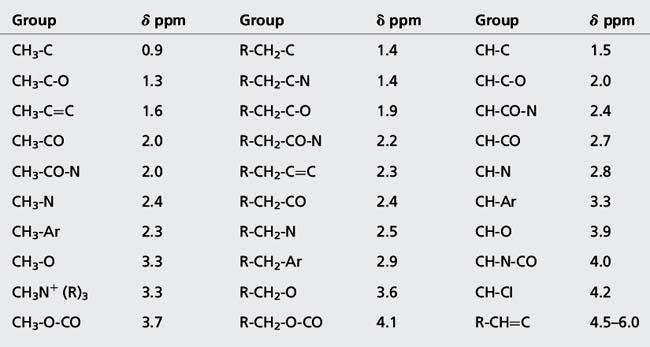
The chemical shift is determined by the extent to which a proton is deshielded by the groups to which it is attached. The more a proton is shielded by the electron density around it, the lower its δ value. If a proton is attached to a system that withdraws electrons from its chemical environment, such as an electronegative group, or to a group which affects its environment by creating a field opposing the applied magnetic field, such as occurs in the case of protons attached to an aromatic ring, its δ value will increase, i.e. it will resonate at lower field (lower frequency) while aliphatic protons will resonate at higher field (higher frequency). It is often convenient to describe the relative positions of the resonances in an NMR spectrum. For example, a peak at a chemical shift of 10 ppm is said to be downfield or deshielded with respect to a peak at 5 ppm, while the peak at 5 ppm is upfield or shielded with respect to the peak at 10 ppm (Fig. 8.4). Tables 8.1 and 8.3 show δ values in ppm for protons attached to some common organic groups.
(i) Alkyl protons such as those in CH3 and CH2 groups not attached to adjacent electronegative groups resonate between δ 0.2 and 2.0 ppm.
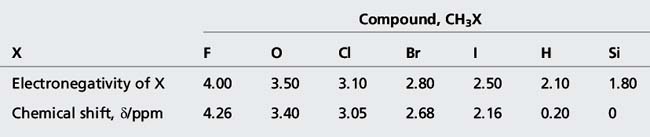
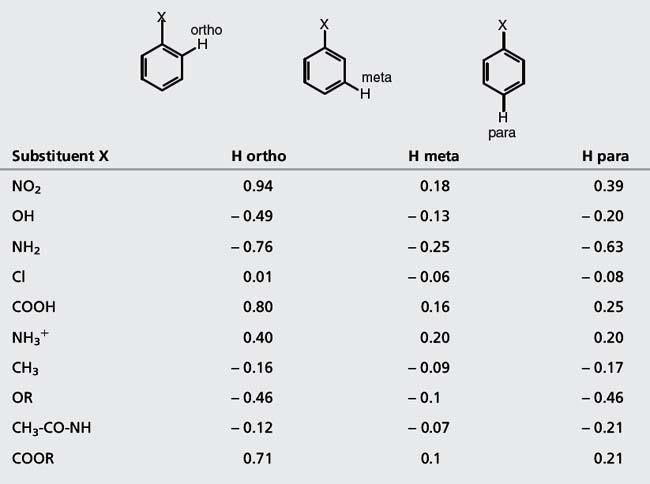
(ii) Protons on CH3, CH2 and CH groups attached to electronegative atoms or groups such as O, N, F, Cl, CN, C=C and C=O resonate between δ 2 and 5 ppm. Electronegative groups attached to the C-H system decrease the electron density around the protons, and there is less shielding (i.e. deshielding) so the chemical shift increases (Table 8.2). These effects are cumulative, so the presence of more electronegative groups produces more deshielding and, therefore, larger chemical shifts, as in the case of CH4, CH3Cl, CH2Cl2, and CHCl3, which exhibit resonances at δ 0.23, 3.05, 5.30, and 7.27, respectively. Protons on an unsubstituted benzene resonate at δ = 7.27, the presence of an electron withdrawing and donating substituent either shields or deshields the protons of a phenyl system, specifically those on the ortho and para position, as shown in Table 8.3. The proton at the meta position is the less affected.
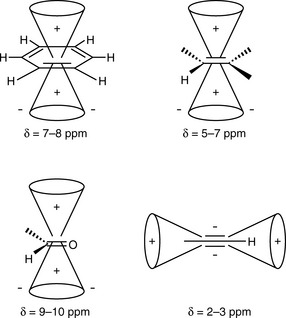
(iii) Protons attached directly to C=C resonate between δ 4 and 7 while protons attached to aromatic rings resonate between δ 6 and 9. Electrons in π systems interact with the applied field, which induces a magnetic field that causes anisotropy (Fig. 8.6). The word ‘anisotropic’ means ‘non-uniform’. Depending on the position of the proton on the π system, it can be either shielded (smaller δ, +) or deshielded (larger δ, −), which implies that the energy required for, and the frequency of the absorption will change.
(iv) Protons that are involved in hydrogen bonding (like those of -OHs or -NHs) are typically observed over a large range of chemical shift values (Fig. 8.7). The more hydrogen bonding there is, the more a proton is deshielded. Hydrogen bonding is susceptible to factors such as solvation, acidity, concentration and temperature and can often be difficult to predict. These H atoms are described to be exchangeable and can be observed by using aprotic solvents (e.g. CDCl3, DMSO, pyridine). Their presence can be confirmed by deuterium substitution experiments in D2O or MeOD.
Table 8.3 Chemical shift values for protons attached to an aromatic ring. The effects of the substituents are either added to or subtracted from the chemical shift for benzene at δ = 7.27
| Substituent X | H ortho | H meta | H para |
| NO2 | 0.94 | 0.18 | 0.39 |
| OH | − 0.49 | − 0.13 | − 0.20 |
| NH2 | − 0.76 | − 0.25 | − 0.63 |
| Cl | 0.01 | − 0.06 | − 0.08 |
| COOH | 0.80 | 0.16 | 0.25 |
| NH3+ | 0.40 | 0.20 | 0.20 |
| CH3 | − 0.16 | − 0.09 | − 0.17 |
| OR | − 0.46 | − 0.1 | − 0.46 |
| CH3-CO-NH | − 0.12 | − 0.07 | − 0.21 |
| COOR | 0.71 | 0.1 | 0.21 |
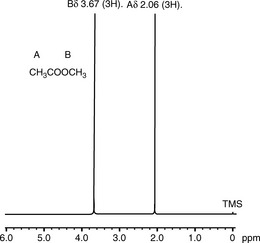
If the NMR spectrum of methylacetate is examined (Figure) it can be seen to yield two signals of the same size at δ 2.06 and δ 3.67, more or less as predicted for CH3CO and CH3OCO groups according to the values in Table 8.1. Determine the frequency difference between the shifts of the protons of the methyl groups of methyl acetate in Hz at field strengths of 60 MHz, 250 MHz and 400 MHz.
Integration and equivalence
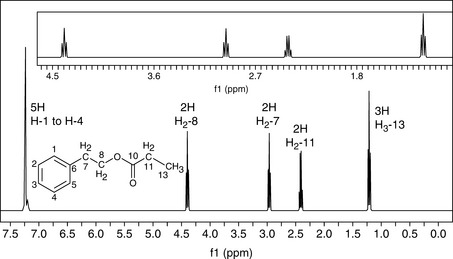
The integration is the area under the peak of a resonating signal which is proportional to the number of protons absorbing radiation at a particular frequency. Three protons will give an area three times that of a signal due for one proton in the same molecule. As shown in the 1H NMR spectrum of phenethyl propionate (Fig. 8.8), the chemically equivalent protons of the phenyl protons resonate as a broad singlet integrating for five protons while the methylene and methyl units integrate as two and three protons, respectively. The integration also provides information on the relative amounts of individual compounds in mixtures or for the levels of impurities in a bulk sample.
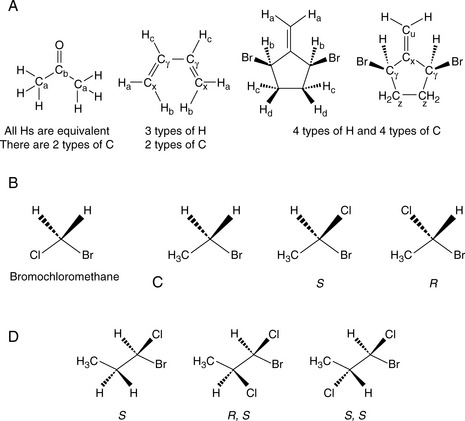
An integral of two or more protons (or indeed with two or more carbons) resonating at similar chemical shifts would indicate magnetic and/or chemical equivalence as observed for a methyl (CH3) unit where all three protons are equivalent (Fig. 8.9A). Methylene (CH2) protons resonating at two chemical shifts would imply chemical and magnetic non-equivalence as exhibited by methylene units vicinal to a chiral centre. In the examples below (Fig. 8.9A–D), the different types of atom are given a subscript; atoms which are equivalent will have the same subscript.
Equivalence defines the three types of protons:
1. Homotopic: Replacement of the groups gives the same product. For example, it doesn’t matter which of the H atoms in bromomethane is replaced with chlorine, and we always get bromochloromethane (Fig. 8.9B). Hence, these three H are said to be homotopic.
2. Enantiotopic: Replacement of the groups gives enantiomers. Consider the H atoms in the methylene group in bromoethane. If we replace one of those H with a Cl, we create a chiral centre. Therefore, depending on which of the two H is replaced, we get one enantiomer or the other (Fig. 8.9C). Hence these two H are said to be enantiotopic.
3. Diastereotopic: Replacement of the groups gives diastereomers. Consider the H atoms in the methylene group in 1-bromo-1-chloropropane. There is already a chirality centre at C1. If we replace one of those H with a Cl, we create a new chiral centre (Fig. 8.9D). Therefore, depending on which of the two H is replaced, we get one diastereomer or the other. Hence these two H are said to be diastereotopic.
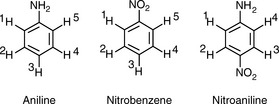
Aniline: In aniline, the 1 and 5 and 2 and 4 protons are equivalent:
Thus the spectrum of aniline would contain:
Nitrobenzene: In nitrobenzene, the 1 and 5 and 2 and 4 protons are equivalent:
< div class='tao-gold-member'>
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree