Introduction to 3D-QSAR



Introduction to 3D-QSAR


With the advancement of computational resources, there is a gradual uplifting of the used dimensions of quantitative structure–activity relationship (QSAR) descriptors. The two-dimensional (2D) and lower-dimensional models suffer from various drawbacks that led to the introduction of 3D-QSAR. This approach has been enhanced with significant advancements in order to study multiple three-dimensional (3D) features of chemicals, establishing a correlation between structure and biological activity. The 3D-QSAR techniques are broadly divided into alignment-based methods [comparative molecular field analysis (CoMFA), self-organizing molecular field analysis (SOMFA), comparative molecular similarity indices analysis (CoMSIA), receptor surface analysis (RSA), and molecular shape analysis (MSA)] and alignment-independent methods [comparative molecular moment analysis (CoMMA), weighted holistic invariant molecular (WHIM) descriptor analysis, VolSurf, Compass, comparative spectral analysis (CoSA), grid-independent descriptors (GRIND)]. The fundamental concept, methodology, and limitations of some of the major approaches are discussed in this chapter to give an overview of this topic.


Keywords


3D-QSAR; comparative molecular field analysis (CoMFA); comparative molecular moment analysis (CoMMA); comparative molecular similarity indices analysis (CoMSIA); comparative spectral analysis (CoSA); molecular shape analysis (MSA); receptor surface analysis (RSA); self-organizing molecular field analysis (SOMFA); weighted holistic invariant molecular (WHIM)


8.1 Introduction


The basic principle of a quantitative structure–activity relationship (QSAR) study is that the deviations in biological response among a series of compounds are accountable for the differences in the structural properties. In the classical QSAR studies, biological responses have been correlated with atomic, group, or molecular properties such as lipophilicity, polarizability, electronic, and steric properties (Hansch analysis) or with certain structural features (Free–Wilson analysis). However, in these techniques, one cannot ignore their limited utility for designing diverse functional new molecules due to the lack of consideration of the three-dimensional (3D) structures of the molecules. As a consequence, 3D-QSAR has emerged as a natural extension to the classical Hansch and Free–Wilson approaches that exploits the 3D properties of the ligands to predict their biological response by employing robust chemometric tools. The 3D-QSAR is a broad term encompassing all those QSAR methods that correlate macroscopic target properties with computed atom-based descriptors derived from the spatial representation of the molecular structures. These approaches have served as a valuable predictive tool in the design of pharmaceuticals and agrochemicals [1–3].


The prime goal of any 3D-QSAR method is to establish the relationship between biological activity and spatial properties of chemicals like steric, electrostatic, and lipophilic ones. The 3D-QSAR methodology is computationally more exhaustive and complex than 2D-QSAR approaches. Normally, it consists of several steps to acquire numerical descriptors from the compound structures:



It is interesting to point out that some methods, independent of the alignment strategy, have also been developed with the progress of 3D-QSAR approaches [4].



One has to understand that the QSAR model is not a substitute for the experimental assays, although experimental techniques are also not free of inaccuracies. However, QSAR researchers are trying to develop a model that is as close as possible to the real one, and for this purpose, the 3D-QSAR techniques have to rely on some basic assumptions, which are illustrated here:



• Binding of a drug molecule or ligand with the receptor is considered directly related to the biological response. Effects on second messengers or other signaling effects between receptor binding and experimentally observed response are not normally considered.


• Molecular properties (physical, chemical, and biological) are encoded with a set of numbers or descriptors.


• It is believed in general that compounds with common structures have comparable properties, and thus they have similar binding modes and accordingly equivalent biological activities and vice versa.


• Structural properties leading to a biological response are usually determined by nonbonding forces, mainly steric and electrostatic ones.


• Another important assumption is that the biological response is shown by the ligand itself, not by its metabolite product.


• The lowest-energy conformation of the ligand is its bioactive conformation, which exerts binding effects.


• The geometry of the receptor binding site is considered rigid, though there are a few exceptions.


• The loss of translational and rotational degrees of freedom (entropy) upon binding is believed to follow a similar pattern for all these compounds.


• The protein binding site is assumed to be the same for all of the studied ligands.


• The major factors that contribute to the overall free energy of binding, like desolvation energy, temperature, diffusion, transport, pH, salt concentration, and plasma protein binding, are difficult to identify and thus are generally ignored.


The 3D-QSAR methods can be classified based on a variety of criteria, as given in Table 8.1. Most commonly and successfully employed 3D-QSAR methods are discussed in the following sections of this chapter.



8.2 Comparative Molecular Field Analysis


8.2.1 Concept of CoMFA


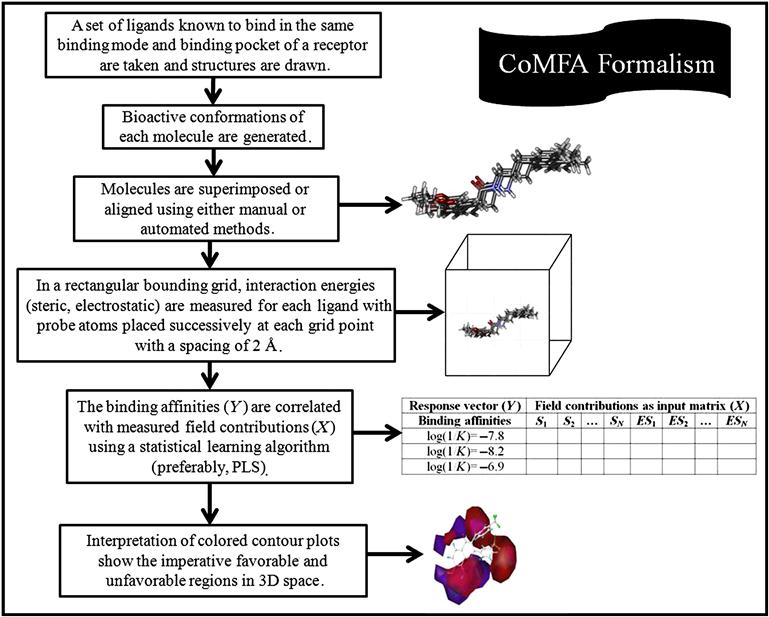
Comparative molecular field analysis (CoMFA) is a molecular field–based, alignment-dependent, ligand-based method developed by Cramer et al. [5], which helps in building the quantitative relationship of molecular structures and its response property. The method mostly focuses on ligand properties like steric and electrostatic ones, and the resulting favorable and unfavorable receptor–ligand interactions. As CoMFA is an alignment-dependent, descriptor-based method, all aligned ligands are placed in an energy grid, and by placing an appropriate probe at each lattice point, energy is calculated. The resultant energy calculated at each unit fraction corresponds to electrostatic (Coulombic) and steric (van der Waals) properties. These computed values serve as descriptors for model development. These descriptor values are then correlated with biological responses employing a robust linear regression method like partial least squares (PLS). The PLS results serve as an important signal to identify the favorable and unfavorable electrostatic and steric potential and also correlate it with biological responses.


8.2.2 Methodology of CoMFA


The formalism of the CoMFA methodology is described next:



a. Structures of all molecules are drawn using any structure-drawing software.


b. The bioactive conformation of each molecule is generated and energy minimization is carried out.


c. All the molecules are superimposed or aligned using either manual or automated methods employed in the working software, in a manner defined by the supposed mode of interaction with the receptor.


d. Thereafter, the overlaid compounds are positioned in the center of a lattice grid with a spacing of 2 Å.


e. In the 3D space, the steric and electrostatic fields are calculated around the molecules with different probe groups positioned at all intersections of the lattice. Computation of the steric field uses the Lennard–Jones equation as follows:


V=LJ4ε[(σr)12−(σr)6]=ε[(rmr)12−2(rmr)6] (8.1)


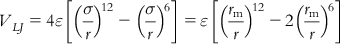image (8.1)


In Eq. (8.1), ε is the depth of the potential well, σ is the finite distance at which the interparticle potential is zero, r is the distance between the particles, and rm is the distance at which the potential reaches its minimum. At rm, the potential function has the value −ε. The distances are given as rm=21/6σ.
Again, computation of electrostatic field follows the Coulombic interaction equation as follows:


E=[q1q24πεr] (8.2)


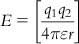image (8.2)

where q1 and q2 denote point charges, r is the distance between charges, and ε is the dielectric constant of the medium.


f. The interaction energy or field values forming a pool of the descriptor/variable matrix are correlated with the biological response data employing the PLS technique, which identifies and extracts the quantitative influence of specific features of molecules on their activity.


g. The results may be expressed as correlation equations with the number of latent variable terms, each of which is a linear combination of original independent lattice descriptors.


h. For visual interpretation, the PLS output is illustrated in the form of interactive graphics consisting of colored contour plots of coefficients of the corresponding field variables at each lattice intersection, and showing the imperative favorable and unfavorable regions in the 3D space, which are closely associated with the biological activity.


The CoMFA formalism is schematically illustrated in Figure 8.1.



8.2.3 Factors responsible for the performance of CoMFA


There are diverse factors that can control the complete performance of the constructed CoMFA model. These are described in the next sections.


8.2.3.1 Biological data


Like any 2D-QSAR method, one has to use precise activity data in order to create a good 3D-QSAR model. The following conditions should be fulfilled for maintaining the accuracy and appropriateness of the biological response data [3,6]:



• All molecules should belong to a congeneric series.


• Compounds should possess the same mechanism of action and the same (or at least an equivalent) binding mode.


• The biological responses of molecules should correlate to their binding affinity, and their specified biological responses should be assessable.



8.2.3.2 Optimization of 3D structure of the compounds


Representing the initial molecular structure is an important issue in 3D-QSAR analysis. This can be done by both experimental and computational approaches. A huge number of experimentally determined crystal structures are accessible in databases like the Cambridge Structural Database [7] and the Protein Data Bank [8]. The obtainable crystal structures present the benefit that some conformational information about the flexible molecule is included. Computationally, the 3D structures can be generated by three methods:



Once the starting 3D molecular structures are generated, their geometries are refined by minimizing their conformational energies using following structure optimization techniques, including:



• Molecular mechanics: It does not explicitly consider the electronic motion, so they are fast, accurate, and can be employed for large molecules like enzymes.


• Quantum mechanics or ab initio: It takes into account the 3D distribution of electrons around the nuclei, and thus it is extremely precise. The identified major drawbacks of this methods are that they are time-consuming and computationally intensive, and they cannot handle large molecules.


• Semiempirical: Semiempirical quantum chemical methods attempt to address two restrictions—namely, slow speed and low accuracy of quantum mechanical (e.g., Hartree–Fock) calculations by omitting certain integrals based on experimental data, such as ionization energies of atoms or dipole moments of molecules. Thus, semiempirical methods are very fast, applicable to large molecules, and may give precise results when applied to molecules that are similar to the molecules used for parameterization. Molecules to be used for semiempirical calculations may contain hundreds of atoms. Modern semiempirical models are based on the neglect of diatomic differential overlap (NDDO) methods like MNDO, AM1, PM3, and PDDG/PM3.


8.2.3.3 Conformational analysis of compounds


The following conformational search methods can be implemented:



• Systematic search (or grid search): It generates all probable conformations by systematically varying each of the torsion angles of a molecule by some increment, keeping the bond lengths and bond angles fixed.


• Monte Carlo: It simulates dynamic behavior of a compound and generates the conformations by making random changes in its structure, calculating and comparing its energy with that of the previous conformation, and accepting the result if it is unique.


• Random search: It generates a set of conformations by repetitively and arbitrarily changing either the Cartesian (x, y, z) or the internal (bond lengths, bond angles, and torsion/dihedral angles) coordinates of a starting geometry of the molecule under consideration.


• Molecular dynamics: It employs Newton’s second law of motion (force=mass×acceleration) to simulate the time-dependent movements and conformational changes in a molecular system, and results in a so-called trajectory showing how the positions and velocities of atoms in the molecular system vary with time.


• Simulated annealing: It theoretically heats up the molecular system under consideration to high temperatures to overcome huge energy barriers, and after equilibrating there for some time using molecular dynamics, cools down the system slowly and gradually to obtain low-energy conformations according to the Boltzmann distribution.


• Distance geometry algorithm: It generates a random set of coordinates by selecting random distances within each pair of upper and lower bounds to form constraints in a distance matrix, which are employed to create energetically feasible conformations of a set of molecules.


• Genetic and evolutionary algorithms: It is based on the concept of biological evolution and initially creates a population of promising solutions to the problem. The solutions with the best fitness scores undergo crossovers and mutations over a time, and proliferate their good distinctiveness down the generations resulting in better solutions in the form of new conformers.


8.2.3.4 Determination of bioactive conformations


The bioactive conformation defines a particular conformation of the molecule in which it is bound to the receptor. The intrinsic forces between the atoms in the molecule, as well as extrinsic forces between the molecule and its surrounding environment, considerably influence the bioactive conformation of the molecule [6]. Bioactive conformations of the compounds can be attained both by experimental and theoretical techniques. Experimental methods for creating bioactive conformations comprise the techniques described.


8.2.3.4.1 X-ray crystallography

The precise 3D structure of the macromolecules can be obtained by this method. Drug–receptor complexes generated by X-ray crystallography logically offer the exact information, but this method has several disadvantages:




8.2.3.4.2 NMR spectroscopy

The 3D structural data is obtained in the solution and is a method of selection when the molecule cannot be crystallized through experimental ways, as in the case of the membrane-bound receptors or receptors, which have not yet been isolated due to stability, resolution, or other issues. The imperative features of this method are:


< div class='tao-gold-member'>

Related posts:

  1. Future Avenues
  2. Newer QSAR Techniques
  3. Validation of QSAR Models
  4. Selected Statistical Methods in QSAR

Stay updated, free articles. Join our Telegram channel
Tags:
Jul 18, 2016 | Posted by in PHARMACY | Comments Off on Introduction to 3D-QSAR

Full access? Get Clinical Tree
Get Clinical Tree app for offline access