Figure 7.1 Illustration of a suspension
Typically, suspensions are coarse dispersions consisting of solid particles (100–50000 nm in diameter) in liquid dispersion media.
Particles and potential energy
To briefly review, when two dispersed particles approach each other, because of inequity between attractive and repulsive forces over distance, there are two net PE ‘wells,’ or minima, where particles have PE optima (the most energetically stable distances from neighboring particles). The minimum furthest from the neighboring particle requires less energy to leave than does the more proximal minimum. With regard to drug delivery systems, this means particles located at the furthest energy minimum are more easily redispersed than are particles at the closer minimum where they are bound more tightly together.
Particle sedimentation and Stokes’ law
As previously mentioned, when particles separate from their dispersion medium, sedimentation of the particles normally occurs. This is not always true, but is the most common scenario. Frequently, then, how quickly the particles settle becomes the variable we wish to control. If settling is slow, measurement and use of the drug delivery system is easier than if particles sediment quickly.
Sedimentation rate of suspension dispersed phases roughly follows Stokes’ law:
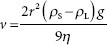
where
v = sedimentation velocity (cm · s–1)
r = particle radius (cm)
ρS = density of solid (g · cm–3)
ρL = density of liquid (g · cm–3)
g = gravitational constant (980.7 cm · s–2)
η = viscosity of the dispersion medium (poise = g · cm–1 · s–1).
Stokes’ law operates under the assumption that the particles are small, perfect spheres that create no turbulence and have no collisions (ideal conditions). Within these assumptions, Stokes’ law applies to suspensoid concentrations of up to about 2%, and so includes most ophthalmic and injectable suspensions. (Keep in mind that the sedimentation velocity, v, can conceivably be a positive or negative value.) A positive sedimentation velocity indicates a downward particle motion. A negative sedimentation velocity indicates an upward motion. When applying Stokes’ law to suspensions the downward (positive) value of v is more often applicable. The discussion of emulsions – the other coarse dispersion – will include application of negative sedimentation velocities, which indicate the dispersed phase is rising. This is a major issue for emulsions, as will be expounded upon later.
Inspection of Stokes’ law indicates the suspensoid will settle if its density is greater than that of the dispersion medium, as illustrated in Figures 7.2 and 7.3. If a dispersion medium of greater density than that of the suspensoid were employed, separation by rising to the top of the preparation would be the hazard. If the suspensoid settles in a compact way, a dense cake, which can be difficult to redisperse, may be formed. It is here that the PE well in which the dispersed phase occupies can dictate redispersability. The ‘compact’ settling of suspensoid demonstrates occupation of the second (closer) PE minimum. This problem will be revisited shortly. For now, it should be kept in mind two issues are important: 1) how quickly particles separate, and 2) how strong the interactions among separated particles are.
Figure 7.2 Gravity influences suspension particles
The effects of gravity can cause suspensoid particles to settle, the rate of which is described by Stokes’ law. The value for sedimentation, v, will be negative, reflecting a downward motion of the dispersed phase. A smaller magnitude of v indicates there will be more time for use of the suspended system before sedimentation occurs.
Key Point
With regard to suspensions, it important to be mindful of 1) particle sedimentation rates, and 2) strength of sedimented particle interactions (cohesion).
A qualitative examination of Stokes’ law reveals a few parameters that can potentially be manipulated to control sedimentation velocity: dispersed particle radius, viscosity of the dispersion medium and possibly the density of the dispersion medium. If the suspended particle size can be reduced (i.e., by trituration), r is reduced, decreasing sedimentation velocity. The viscosity disparity between the dispersion medium and dispersed phase densities may be reduced if the dispersion medium viscosity can be altered or the medium completely changed. This is feasible with regard to preparing drug delivery systems as a whole. Again, this can be done if it does not compromise the safety, efficacy and general physical parameters required by the drug delivery system. A common solution is to increase the dispersion medium viscosity, decreasing v. One method to increase viscosity is to employ hydrophilic colloids as parts of the coarse dispersions, which have viscosity-increasing properties, as described in Chapter 6. Sometimes apparent solutions to remedy large sedimentation velocities are not helpful though. For example, reduction in suspensoid particle size (if this is a potential option) also increases total dispersed phase surface area, causing Gibbs’ free energy (∆G) to increase:
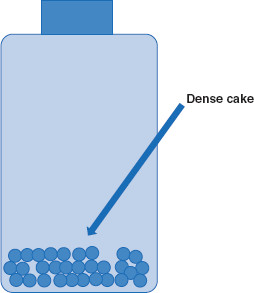
Figure 7.3 Formation of a dense cake due to suspensoid settling
As suspensoid particles settle, they threaten to form a dense cake if particles pack too tightly. This outcome can be avoided if particles are induced to approach each other no closer than the distance represented by the outer energy minimum.
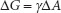
where
∆G = free energy change
γ = interfacial free energy
∆A = change in interfacial area.
As the particle size is reduced (such as is accomplished through trituration), the free energy increases. A large free energy indicates that the system is thermodynamically unstable and that it will tend to spontaneously move in the direction of interfacial area reduction (e.g., through crystal growth and/or precipitation) to decrease free energy. Interfacial tension (γ) can be reduced to attempt to offset the increase in surface area, such as by addition of surfactants, but it is unlikely to achieve a large enough impact – one that would completely negate the change in surface area – providing a γ value near ‘zero.’ Therefore, reducing particle size in an effort to decrease sedimentation rate may sometimes not be helpful. This can also be true for attempts to favorably alter other Stokes’ law parameters. It may be impractical to change the density of either the drug (ρS) or dispersion medium (ρL), so this potential remedy is not commonly employed.
The prior discussion helps understanding that, in many cases, sedimentation of the dispersed phase is going to happen, but it does not mean all is lost. The task is to decide the best measures to employ in order for the delivery system to function as it was intended, working around the inevitability of settling. In general, this is a question of whether to try to keep the suspensoid dispersed as long as possible, or to allow it to settle, but control the structure the particles assume once they settle.
Formation of a cake (sediment)
The dilemma for dealing with suspensions then can become the ‘redispersability’ of the sedimented particles. Once settled on the bottom of a container, particles threaten to crystallize, creating a dense cake or aggregate (the ‘compact’ settling) that can be extremely difficult to redisperse. Some of the choices described above pertain to early stages in the sedimentation process and involve manipulation of sedimentation velocity (v). Though it may seem counterintuitive, it actually may be advantageous either to increase or decrease sedimentation velocity, depending on the ultimate system design. If suspension particles are more dense than the suspension medium, they are destined to settle into a structured crystalline cake. What parameters influencing crystal growth come into play once a suspension has settled? Two include temperature fluctuations and Ostwald ripening.
Recall in Chapter 3 it was said that all materials are soluble to some extent in a given solvent. A suspension’s behavior can be viewed as a dispersion of a solid in a saturated solution. Temperature fluctuations then can affect this nominal ‘solubility.’ The outcome is dependent on the heat of solution, ∆Hsoln. When the insoluble particles settle to the bottom of the container, forming a dense cake, crystal bridges between particles can develop. Crystallization starts with one particle, then bridges to others. Using this ‘saturated solution’ model, the effect of temperature on crystal growth is illustrated with the van’t Hoff equation:
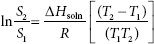
where
S1 = solubility (i.e., g . mL–1) at temperature T1
S2 = solubility at temperature T2
∆Hsoln = heat of solution (cal . mol–1)
R = 1.99 cal . mol–1
T = temperature (K).
When rearranged to focus on solubility, the form is:
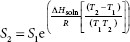
When ∆Hsoln is positive, which is true when S2 > S1, the ‘solubility’ increases with increasing temperature. Adding heat to the system, moving from T1 to T2, increases solubility, from S1 to S2. When ∆Hsoln is negative, which is true when S1 < S2, solubility decreases with increasing temperature, so adding heat to the system will decrease solubility. What does this mean? First, that solubility is a function of the heat of solution, so temperature can positively or negatively influence the degree of solubility viewed here in a thermodynamic way. Second, that variation in temperature causes transient increases and decreases in ‘solubility’. By changing S, especially with several fluctuations, more opportunities arise for particles to sediment, and once it begins, simply returning to an initial temperature does not guarantee reversal of crystallization. Temperature fluctuations can initiate and accelerate crystal growth within the sediment.
Key Point
Two important components regarding suspension caking include temperature fluctuations and crystal growth via Ostwald ripening.
Ostwald ripening is a process by which particles that do arise, such as those from temperature fluctuations, tend to become larger and tend to deposit on progressively larger particles at the expense of smaller particles. This process of creating larger particles is thermodynamically favored over retention of small particles because small crystals have a larger surface area-to-volume ratio than do large crystals. Ostwald ripening is described by the Kelvin equation (also called the Ostwald–Freundlich equation):
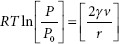
where
P = vapor pressure over a curved surface
P0 = vapor pressure over a flat surface
γ = interfacial free energy
v = molar volume
r = radius
R = 8.314 × 107 erg/mol K
T = 298 (K).
The Kelvin equation pertains to boundaries between two phases, relating surface tension of a boundary with its curvature. It tells us that vapor pressure over a curved surface is greater than over a less curved surface. Smaller spheres have increased curvature, and so increased vapor pressure (escaping tendency). How does this relate to the dispersed phase particles? Stated in another way, small particles have better ‘solubility’ than large particles. So, small particles disappear and larger particles grow at the expense of the small particles. This is not a ‘thermal’ process – it cannot be avoided even under conditions of constant temperature. The result pertinent to suspensions is that this process leads to caking. Caking is dense packing of particles through formation of rigid structure.
So, to summarize, considering both the van’t Hoff and Kelvin equations, it can be gathered that a major obstacle to maintaining usefulness of suspensions is the reinforcement, or amplification, of the strength of interparticulate cohesion, especially at distances in the range of closer PE minima (i.e., intermolecular interactions). These, in turn can be temperature-fluctuation dependent.
Conceding the inevitable: Management versus avoidance
As mentioned previously, when settling occurs, the dosage form is not necessarily ruined if the conditions under which the particles settle are controlled. What can be done to ensure the settled suspensoid (particles) can be reconstituted with reasonable effort? First, it must be conceded that ‘interactions’ among components of complex pharmaceutical suspensions are predestined. However, there are choices of how to exert some control over sedimentation, depending on what is most suitable for the particular delivery system. The two potential courses of action include: 1) attempting to avoid suspensoid interactions or 2) trying to manage the interactions. Ultimately, the goal of either path is to keep the suspension delivery system usable. Avoidance has the aim of precluding, or at least delaying, suspensoid interactions. Management has the aim of optimizing the way in which the suspensoid settles. First, two terms must be defined. Flocculation is the creation of floccules. Floccules are flakes, or loose, irregularly shaped particles. When they settle they do not compact well. Deflocculation, then, is the antithesis: the intentional creation of a coagulated system. Though deflocculation may sound counterproductive, there are some situations when it is the better alternative. Variations of either extreme are also commonly employed.
Flocculation and deflocculation
Creation of a flocculated system is the approach to precluding or delaying interactions among the components of a suspension and can involve use of a structured vehicles to slow sedimentation rate (velocity). Deflocculation is intentional coagulation of the system and also can employ structured vehicles.
Flocculation is a method of prohibiting settled particles from creating a structured crystalline cake so that they exist as loose aggregates. Flocculation is achieved by creating charge and/or stearic irregularities on the surfaces of suspension particles (causing them to act as ‘flakes’ or ‘fluff’), while retaining some repulsive energy between particles. The goal is to force irregular packing of the particles when they settle, with large interparticulate distances, allowing weak attractive interactions among the particles. The attractive interactions are weak enough to allow for physical redispersion to be possible. Flocculation can be used to resist the compression, induced by gravity, borne by suspended particles. Intentionally causing flocculation of a suspension is one method by which resuspendability can be ensured.
Recall from Chapter 6 the PE of interaction in dispersions, VT = VA + VR + VS, where VT = total interaction energy, VA = van der Waals attractive energy, VR = electrostatic repulsion via the electrical double layer, and VS = steric and solvent repulsion. Also recall that repulsive forces are shorter-range than are attractive forces (Figure 7.4), which creates two PE minima that are energetically favorable separation distances for particles to occupy. The discussion in Chapter 6 was in regard to colloidal dispersions, but the concepts are also applicable to suspensions.
The outer PE minimum (approximately 1000–2000 Å apart) is where successful flocculation holds loosely aggregated particles and the inner PE minimum is where coagulation is likely to occur. If particles are held at the ‘flocculation’ minimum, it can be seen by comparing the PEs, redispersion of the suspensoid is less energetically demanding and more likely to be feasible than for particles that have moved to the coagulation energy well. So, when it is decided a suspension should be stabilized by flocculation, the goal is to direct the particles to the outer PE well where they will hopefully remain. Figure 7.5 illustrates the concept of a flocculated suspension.
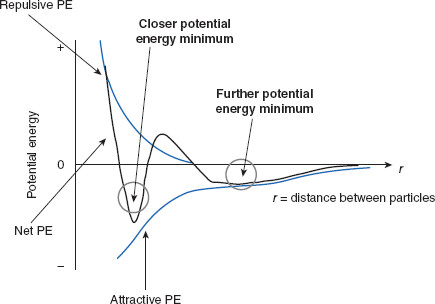
Figure 7.4 Two potential energy (PE) minima where particles may reside
Particles with a separation distance at the outer energy minimum have the smallest PE of the two minima, and so are more easily redispersed than those that are separated by the distance denoted by the closer PE minimum.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


