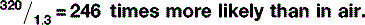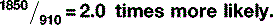Chapter 9 Diagnostic imaging
Introduction
Over the past 30 years, it has become possible to image not only bone but soft tissues as well, revolutionizing the diagnosis and management of injury and disease processes. These changes have, inevitably come at a price. Whereas a new x-ray machine can be purchased and installed for under $100 000, the cost of magnetic resonance imagers start at over $1 500 000 and positron emission tomography costs many times more. The recent development of ultrasound as an imaging modality has started to drag costs back and offer some relief to over-stretched medical budgets. However, as patient expectations and the population age profile both increase, clinicians are being forced into cost/benefit decisions unknown to the previous generation (though not to private manual therapists working with self-funding patients). They must also now become familiar with a raft of different imaging modalities based on a much wider array of underlying principles (i.e. physics) and understand how and why their patients would benefit from referral.
The x-ray machine
It is now time to understand how those elements work in practice.
Thermionic emission
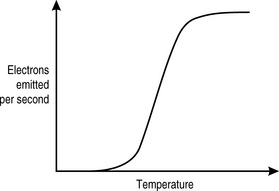
In an x-ray machine, the thermionic filament is traditionally made from tungsten. This element is particularly useful in this context, not only because it is relatively inexpensive and easily available but because of its work function profile (Fig. 9.1) and its high melting point (3 683K). When the x-ray machine is switched on, the filament is heated only slightly by a current that is low enough that it is below the threshold for thermionic emission. It is further protected from too rapid heating by a thermistor, described in Chapter 8 as a device whose conductance increases with temperature.
Once the filament current is high enough for thermionic emission to occur, we can see from Figure 9.1 that it takes only a very small increase in temperature (produced by the heating effect of the current) to effect a very large increase in the number of electrons produced. There is an upper limit to electron production. This is determined by the mutual repulsion between the electron cloud and the electrons within the filament that are trying to escape, the space charge effect. Beyond this point, very few further electrons are produced, regardless of how much additional current is introduced. The risk of vaporizing the tungsten also increases, thus limiting the effective filament current to below this level.
WORK FUNCTION
You have, of course, already encountered this concept in Chapter 6 when discussing the photoelectric effect. Work function is defined as the minimum amount of energy required per electron to remove it from the surface of a solid. It is given a symbol, the Greek letter phi (Φ).
Where T is absolute temperature and e is the base of the natural logarithm (if you do not already know what this is, it matters not, just accept that it is a constant = 2.718).
Electron production
All these value combinations produce the same number of electrons. If we recall that an amp is a coulomb per second, then:
There are 1.6 × 10−19 C per electron, therefore there are:
Therefore, 100 mC has 6.25 × 1017 electrons.
Electron energy
This involves having electrons with high energies, which means in turn that they must be accelerated to a high speed. This is done by sealing the filament and the tungsten target at which the electrons will be fired in a sealed glass cylinder containing a vacuum. This comprises the x-ray tube. The absence of air prevents the electrons interacting with the molecules of nitrogen, oxygen, carbon dioxide and trace elements, which would only produce low-energy x-rays (small nuclei, therefore lower electron shell binding energies) and limit the number and energy of those electrons reaching the target.
It does this by being wired to the next x-ray component, the autotransformer. Although this works on a subtly different principle from the transformers that we considered in Chapter 7, the underlying physics remains the same – a primary voltage induces a magnetic field in a shared ferromagnetic core. This, in turn, induces a secondary voltage. By adjusting the ratio of the number of coils around the core in the primary and secondary circuits, the secondary voltage can be increased or decreased compared to the primary.
High-voltage capacitors are then used to smooth the circuit to deliver a constant, controllable, high voltage across the vacuum between cathode and anode (Fig. 9.2).
Production of x-rays
Although in dental x-ray machines, the low exposures mean that a fixed target can be used, in medical machines, capable of imaging a pelvis, if the electron beam were always centred on a single spot, that area would soon become damaged and degraded and the (expensive) tube, ruined.
Heel effect
The x-ray target must also be carefully shaped (Fig. 9.3A) in order to direct as many of the x-rays as possible towards the target (patient) rather than randomly, in which event they will be absorbed by the protective lead casing of the tube rather than used for their intended purpose. The edge of the rotating anode is bevelled – usually at an angle of about 6° – in order to direct the x-rays towards the aperture, the hole through which the radiation is directed at the patient. Metal sliding panels called collimators can cover all or part of the aperture to further limit the spread of the beam and to ensure that only the targeted area is exposed.
Unfortunately, for every innovation there is a consequence, and the sloping of the target means that the x-rays that are produced have varying amounts of tungsten to penetrate before emerging from the target and therefore a higher chance of interacting with other tungsten atoms before emerging. This means that the x-ray beam that emerges from the aperture will be more intense on the cathode side than the anode side, the heel of the target (Fig. 9.3B). This will have an effect on the x-ray penetration of the patient and the final image, which can be under-exposed on one side and over-exposed on the other.
By contrast, when taking chest x-rays, the upper thorax is thinner than the lower. By positioning the cathode inferiorly, this effect can be minimized. This effect applies, to some extent or other, to almost every body part from the foot (the calcaneus is thicker than the metatarsals and phalanges) to the cervical spine (C7 is larger than C1 and surrounded by denser soft tissues).
Quantity of x-rays
A number of factors can affect the quantity of x-rays reaching the patient. We have already discussed mAs, which is directly proportional to the quantity of x-rays (if the mAs is increased, the number of electrons hitting the target increases as does the number of x-rays produced).
Quality of x-ray
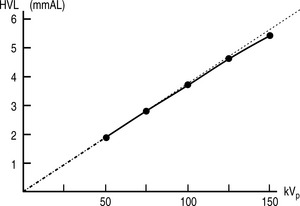
There are, once again, several factors that can affect the quality of x-rays. Before discussing these, it is worth noting that neither mAs nor SID have any effect on the quality of the beam, only the quantity of x-rays produced. kVp does affect the quality, as might be expected. Increasing the energy of the electrons hitting the target results in the production of more high-energy x-rays, which means the spectrum of x-ray energies is shifted to the right and more high-energy characteristic x-rays will be produced. There is no direct linear relationship between kVp and HVL; however it is approximately proportional (Fig. 9.4).
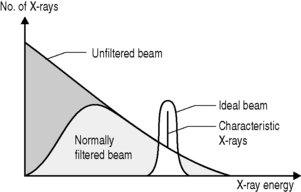
As is implicit from the discussion of HVL, filtration can also affect the quality of the beam. If a filter is placed between the x-ray source and the target then a greater proportion of low-energy x-rays will be attenuated than high-energy x-rays. Although this will reduce the quantity of x-rays reaching the patient, it will increase their quality. The most commonly selected material for x-ray filters is aluminium; it is cheap and, because of its relatively low atomic number (Z = 13), allows through a relatively high proportion of high-energy x-rays but will stop low-energy x-rays through the photoelectric effect.
There are two types of filter employed in the x-ray room. Inherent filtration is included in the x-ray tube as is a combination of the glass screen over the aperture and added aluminium, usually a thin sheet placed between the target and aperture to remove as many low-energy x-rays as possible without significantly affecting the quantity of photons. As this filtration is fixed, its effects can be incorporated in the exposure protocols for a given machine. The effects of this collimation are shown in Figure 9.5.
The factors that affect x-ray quality and quantity are summarized in Table 9.1.
Table 9.1 Factors that affect the quality and quantity of x-rays
| Factor | Effect upon | |
|---|---|---|
| X-ray quantity | X-ray quality | |
| mAs | Increases in direct proportion | None |
| SID | Decrease according to inverse square ratio | None |
| kVp | Increases in proportion to the square of the ratio of the increase | Increases approximately proportional |
| Filtration | Decreases exponentially | Increases |
Patient exposure
In Chapter 8, we examined the ways in which x-rays can interact with matter. In diagnostic radiography, only two of these are important: the Compton and photoelectric effects. They are, however, only important in a negative sense – it is the x-rays that pass through the patient without undergoing any interaction with matter that form the image of the patient in which we are interested.
The effective atomic number of different soft tissues is dependent on the relative proportion of atoms within their matrix. Bone, for example, is made from hydroxyapatite, which contains calcium (Z = 20) and phosphorus (Z = 15). It has an effective atomic number of 13.8. By contrast fat, which is principally composed of hydrogen (Z = 1) and carbon (Z = 6), has an effective atomic number of 6.3 (other soft tissues average 7.4).
Therefore, photoelectric absorption is:
The chance of interactions is also related to the mass density of the material — bone is denser than fat and therefore there are more atoms with which the x-rays can interact. So, the probability of x-ray interactions (of either type) is directly proportional to the mass density of the material (Table 9.2). This is why interaction is much more likely in lung tissue than in air, despite the fact that their effective atomic numbers are almost identical. The actual chances of either Compton scattering or the photoelectric effect occurring in lung tissue is:
Table 9.2 Effective atomic number and mass densities of different body materials
| Tissue type | Effective Z | Mass density (kg m−3) |
|---|---|---|
| Bone | 13.8 | 1850 |
| Muscle | 7.4 | 1000 |
| Fat | 6.3 | 910 |
| Lung | 7.4 | 320 |
| Air | 7.6 | 1.3 |
Therefore, the chances of the photoelectric effect occurring in bone are actually:
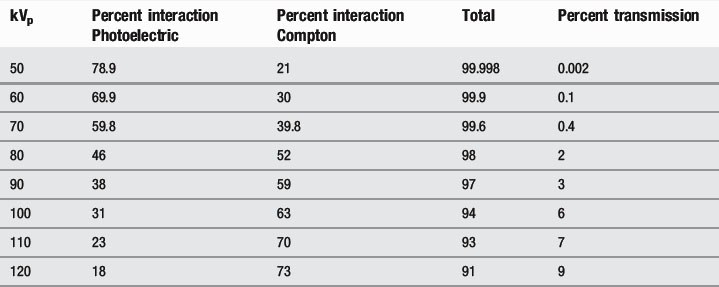
This means that, at lower kVp values, the photoelectric effect dominates, whilst, at higher values, the Compton effect is more important. Increasing the kVp also increases the percentage of x-rays that pass through the patient (Table 9.3).
Table 9.3 Effect of decreasing kVp on Compton scattering, photoelectric absorption and x-ray transmission
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


 DICTIONARY DEFINITION
DICTIONARY DEFINITION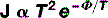

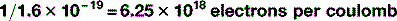
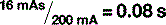
 CLINICAL FOCUS
CLINICAL FOCUS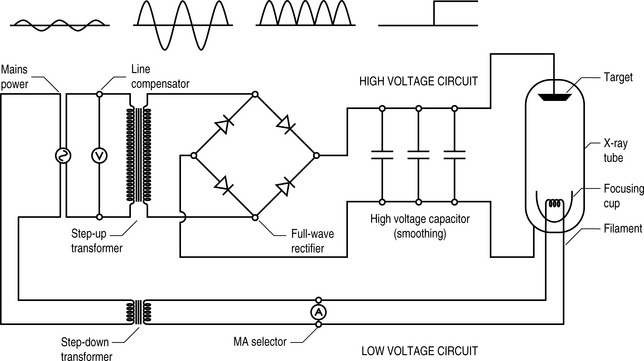
 Fact File
Fact File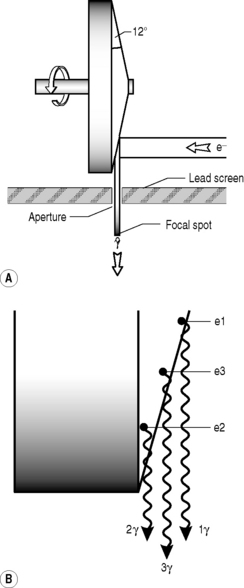
 CLINICAL FOCUS
CLINICAL FOCUS Fact File
Fact File DICTIONARY DEFINITION
DICTIONARY DEFINITION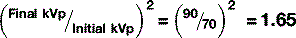
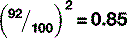

 CLINICAL FOCUS
CLINICAL FOCUS