Computational Chemistry
The expansion of theoretical chemistry and molecular modeling analysis has been assisted by advanced computational platforms. Computers not only can be used to solve complex chemical equations, but also to provide a suitable graphical viewer package to hypothetically visualize simulated operations and their output. Hence, computer technology proves to be an indispensable tool for carrying out molecular modeling operations. In fact, one can easily run such a job using the default values specified by the provider of a specific program. In order to interpret the outcome of a molecular modeling operation, one needs to have sufficient knowledge of the theoretical bases of the operations involved. In this chapter, we have attempted to provide some basics of different aspects of computational chemistry, where computer applications are crucial. In addition, we have provided the basic theoretical foundation involved in such processes, on the assumption that readers are novices in this field. With a clear conception of the theoretical bases, one can not only interpret the results of such modeling operations, but also modify the process variables in accordance with the needs in question. While certain processes might give appreciable results for certain groups of chemicals under defined criteria, it may be the case that other processes may fail or not even be applicable. Hence, readers are advised to achieve a basic theoretical insight of the molecular modeling operations in the light of computational algorithms instead of considering them a “black-box tool” for obtaining data.
Keywords
Computer; simulation; in silico; molecular mechanics (MM); molecular dynamics (MD); semiempirical quantum mechanics
5.1 Introduction
Advancement in any scientific discipline proves fruitful when it is supplied with suitable media of operations that make the science unambiguous to all its users. The development of various computer applications has enriched the operations involved in different technical and scientific processes. As in other scientific disciplines, the deployment of computer workstations has instituted a revolution in the research and development of chemistry. Modern medicinal chemistry employs several computational applications in solving simple to complex problems with a high level of accuracy. Nowadays, computers have become an inevitable tool in drug discovery and drug development. The use of desktop computers has enabled the solving of complex chemical problems while requiring little specialist expertise at the laboratory-scale operations. The computer technology has enhanced the research in theoretical chemistry by allowing not only a platform for solving complex chemical equations and models, but also suitable graphical interfaces for a better understanding of the involved chemical phenomena. The quantitative structure–activity relationship (QSAR) methodology employs the quantification of molecular structures followed by the development of mathematical correlation with the aim of predicting the activity/property/toxicity of untested or new chemicals. The entire operation, starting from encoding of structural information to model development, and validation as well as prediction, employs a significant amount of data that can be reliably operated using suitable computer programs. At times, the predicted features have been found to be more accurate and reliable than experiments considering a higher degree of error involved in experimental studies. There are different technical aspects that must be considered while using computers as an essential component in the molecular modeling epitome, and it is thus obvious that the assistance of an expert in computational chemistry would be necessary while dealing with such in silico tools. However, it will be very helpful to have some basic insight regarding the fundamental theory involved in such operations based on how developers design their products. Hence, we shall highlight the basic theories involved in defining some of the chemical attributes, like molecular orbital (MO) theory, principles of molecular mechanics (MM), and quantum mechanics along with a focus on the avenues of their implementation in various types of algorithms.
5.2 Computer Use in Chemistry
Discoveries and developments in chemistry have come a long way since the time of the Greek philosopher Thales (sixth century BC), who hypothesized that simple elements (earth, water, air, and fire) form chemical substances. With the passage of time, knowledge of the molecular composition, structural features, arrangement, and properties of chemicals have been developed, and computers have become an essential part of it by acting as a tool of documentation, analysis, and representation. It is not preposterous to state that the incorporation of computer technology has added significant momentum to the research of theoretical chemistry. However, it should be remembered that discovery and development of the theoretical bases are of primary importance, and computers act as an implementation tool. By the use of suitable software and hardware technologies, developers encode the theoretical information by applying definite algorithms, which makes the theory easily applicable to the users. Hence, any limitations or approximations of a software platform entirely depend upon the developer, not the theory itself. Now, with the incorporation of various applications of computers in solving chemical problems, several terms are used. Theoretical chemistry broadly corresponds to the mathematical depiction of chemical information, while computational chemistry is used to denote a collection of techniques employed to solve problems of chemistry using computers.
Now, it is evident that computers have played an essential part in almost all types of technical operations, including various chemical analysis systems like spectroscopy and chromatography, which provide analog support to the system. However, in this chapter, we shall focus on the use of computers in enhancing the theoretical aspect of chemistry. Another term, molecular modeling, is also used to define the same formalism encompassed by computational chemistry. Technically, the word model refers to an idealized depiction of a system, and if we consider mathematical formalism, a model is a way of providing the calculations and predictions of a system [1]. Hence, molecular modeling covers several aspects of theoretical chemical computation and the reasonable prediction thereof. The sphere of theoretical chemistry can be computational as well as noncomputational, depending upon the mathematical basis developed to encode a chemical problem. Hence, the noncomputational part concerns the formulation of analytical expressions for molecular properties, and when sufficient mathematical background is developed in addressing a chemical problem, the algorithm is executed using computational tools. Therefore, we can observe an interdisciplinary embellishment of chemical theory put into strong mathematical formalism, followed by computational encoding. The implementation of computational technology in theoretical chemistry can be broadly viewed in three aspects: namely, visualization, computation, and analysis. In the next sections, we shall present a brief overview of different molecular modeling operations performed with the assistance of computers.
5.2.1 Visualization
Computers strengthen general understanding of chemicals by providing a suitable graphical visualization interface. This encompasses the visualization of single chemical structures to the hypothetical interaction pattern between the receptor and ligand.
5.2.1.1 Structure drawing
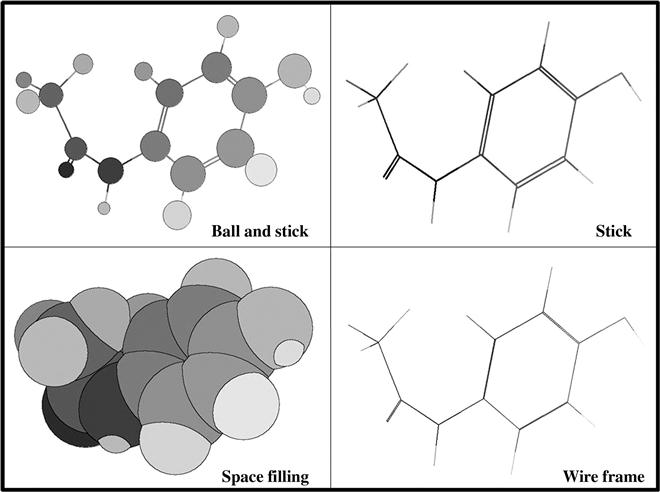
Such tools allow the drawing of a chemical structure in a workspace within the desktop. By using the sketching tool, a user can draw structures employing various chemical bond tools, atoms, chains, ring-template, and other items. The structures are encoded in the form of coordinates that are graphically converted into images on the computer screen. The same structure can be displayed in different graphical forms, some of which include Corey–Pauling–Koltun (CPK), stick, ball-and-stick, space fill, mesh, and ribbon [2]. Of these, the ribbon type of representation is usually employed for large molecules like proteins and nucleic acids. Figure 5.1 shows several graphical depictions of the paracetamol (p-acetamidophenol) molecule. Most of the commercial structure-drawing packages assign a specific color coding to each type of atom, a system that is editable by the user. Examples of some chemical-drawing packages are ChemDraw (http://www.cambridgesoft.com/Ensemble_for_Chemistry/ChemDraw/), IsisDraw (a product of MDL Information Systems, Inc.), ChemSketch (http://www.acdlabs.com/products/draw_nom/draw/chemsketch/), and MarvinSketch (https://www.chemaxon.com). Many of these packages also allow the computation of various properties along with the drawing facility. Not only that, most of the software packages provide other tools that perform functions such as checking the structure (valence, bond order, etc.) and generating IUPAC names.
5.2.1.2 3D visualization
By using a suitable graphical conversion package, the user can obtain a three-dimensional (3D) visualization of the structure. Many of the molecular modeling packages allow the simple and direct conversion of a two-dimensional (2D) structural format into 3D when a 2D structure is opened or pasted into its drawing area. Examples of some software platforms that allow 3D viewing of molecular structures include Chem3D (http://www.cambridgesoft.com/Ensemble_for_Chemistry/ChemDraw/), Discovery Studio (http://accelrys.com/products/discovery-studio/), Sybyl (http://tripos.com/index.php), Hyperchem (http://www.hyper.com/), and Maestro (http://www.schrodinger.com/Maestro/). However, it may be observed that the visualization plane of the computer is 2D, and hence a 3D molecular view is generated by making some modifications to the axes. This is achieved by making less dense coloring of the atoms/bonds away from the viewer or by reducing their visualization bond length.
5.2.1.3 Visualization of ligand–receptor interactions
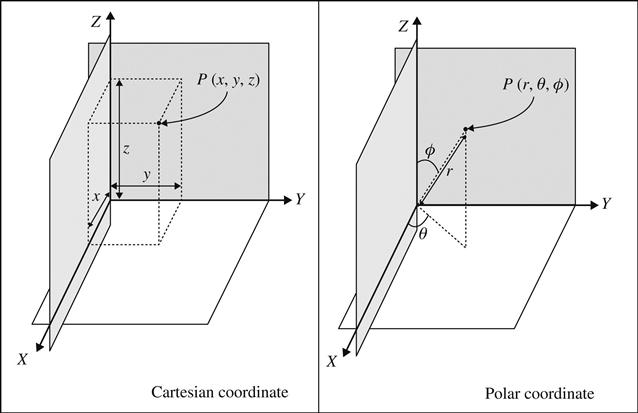
Visualization of ligand–receptor interactions is a very useful functionality that provides a 3D graphical presentation of a hypothetical interaction between the ligand and the receptor molecule to the viewer. Since the biological system encountered by a query molecule is entirely 3D in nature, such visualization helps in predicting the nature of molecular interaction at the receptor binding site. Hence, by providing a suitable interface to the user, computers allow the storage of compound information in terms of their structure. Various formats are available to save the molecules, including .cdx, .mol, .skc, and .rxn. Drawing chemical structures is the beginning of any molecular modeling operation, since the drawings are used as input queries to carry out further analyses. It can be observed that the visualization of a chemical structure in a computer window is entirely a part of graphical conversion. The structures are represented by Cartesian/polar coordinates, which are being processed by software algorithms to be portrayed in different forms and shapes. Moreover, the user must understand that any kind of visualization under the molecular modeling paradigm is basically a form of representation for designing and communication purposes only, not a realistic depiction.
5.2.2 Calculation and simulation
Following the drawing/sketching of chemical structures, the next most important part of molecular modeling analysis involves the quantification of chemical information. These include a number of simple to complex theoretical analyses. Simply stated, with the aim of exploring the chemical attributes at the atomic and electronic levels, scientists have developed different theories on molecular environment by combining their knowledge of physics, chemistry, and mathematics. Such theories involve lengthy and intricate molecular mechanical and quantum chemical calculations to characterize the chemical nature at the electronic level. The use of computational programs has enabled such calculations to be done in less time with a good amount of reliability and accuracy. In other words, computational chemistry tools allow users to perform complex analysis just by providing some simple commands and other interfaces. Following the analysis, the derived features can be exploited in several aspects of analysis, like in a chemical characterization project, or as independent variables in QSAR analysis. With the progress of research in chemistry, various other theories of quantitative structural depiction have evolved. By the use of a suitable logical algorithm, computers can easily calculate many such molecular attributes—namely, molecular topology, geometric features, thermodynamic properties, and others. One more potential application of using computer technology to explore the chemical field is in drug–receptor studies. A number of techniques [namely, molecular docking studies, pharmacophore development, 3D-QSAR like comparative molecular field analysis (CoMFA) and comparative molecular similarity indices analysis (CoMSIA), etc.] attempt to find the essential structural requirements necessary for eliciting the biological activity of a ligand in a hypothetical 3D environment. Hence, the calculation of chemical features by employing computer applications can be viewed in the following four divisions:
It can be observed that the abovementioned operations are linked to each other; for example, the computation of properties like charge, electrostatic potential, and molar refractivity is done after the energy minimization operation. In this chapter, we shall discuss the different aspects of conformational analysis and energy minimization using molecular and quantum mechanical calculations.
5.2.3 Analysis and storage of data
Computers are well known for their ability to process and analyze a large amount of data using a provided mathematical algorithm. Quantification of chemical information and the analysis thereof yield a significant amount of mathematical data, and these operations are properly done using various computational applications. Before the 1960s, the documentation and analyses of the QSAR technique was practiced without the use of computers. However, with the passage of time, the number of chemicals, end points, and descriptors has increased and needed a suitable platform for (i) storage, (ii) processing, and (iii) online availability of data. In order to pursue the analysis of chemical data, several mathematical techniques and suitable statistical measures are combined and used as in silico computational tools. Many of these tools allow the development of quantitative mathematical models employing techniques such as multiple linear regression (MLR), partial least squares (PLS), linear discriminant analysis (LDA), and genetic function approximation (GFA), followed by statistical validation; that is, computation of different validation metrics to judge the quality of the developed equation. Hence, the support provided by computers toward the analysis of chemical data can be categorized in the following ways:
2. Development of predictive models
Many commercial software packages (e.g., Accelrys software) combine different features of molecular modeling like computation of chemical properties (descriptors), followed by an option for model development and validation, and finally storage of the analyzed data in a specified format. Currently, with the availability of suitable computers, it is possible to carry out virtual screening of library data that contains several thousands to millions of chemicals.
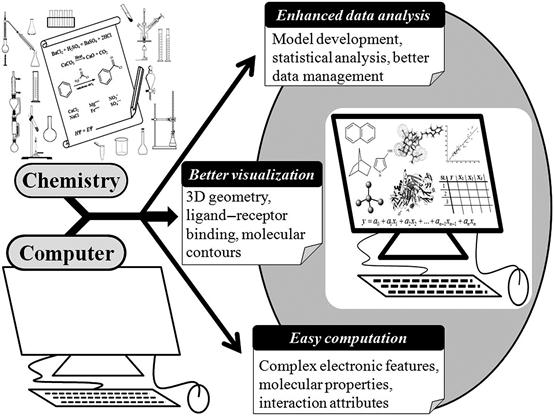
Finally, we would like to comment that by the use of suitable computer programs, it is possible to carry out various molecular modeling operations in a more rational and reliable way, eliminating possible sources of error. Using an efficient computer facility, a large amount of data can easily be processed in a short period of time. However, remember that computers do not and cannot replace any chemical experimentation or synthesis methodology; rather, it promotes molecular modeling analysis by providing a suitable platform to the experimental results toward the design and development of a desired, better chemical entity. Figure 5.2 depicts the privileges provided by various computational tools to facilitate computational chemistry analysis.
While performing complex chemical calculations, such as molecular mechanical, quantum chemical, and semiempirical, remember that the numerical solution provided by any platform cannot be assumed to be the exact or ultimate one, since each of these operations is being executed under several postulates or approximations. Hence, it is wise to decipher the results (i.e., extracted chemical information) with a consideration of the assumptions involved during the calculations. If the chemist identifies any error in the calculation, that fact can be attributed to the algorithm employed or, more specifically, to the platform used but not to computers, which are blind boxes that process information based on the instruction fed to them.
5.3 Conformational Analysis and Energy Minimization
5.3.1 The concept
The term conformation refers to an arrangement of atoms in a molecule, which is interconvertible by rotation about single bonds. The nature of a covalent bond depends upon the state of orbital hybridization between the participating atoms. Since we know that different types of chemical bonds are characterized by specific energy values, free rotation about the sigma bond (σ), such as the carbon–carbon single bond, might induce changes in energy of the whole molecule, leaving it in a favorable or unfavorable energy condition. Now, if a molecule undergoes various molecular arrangements in space, questions might be asked regarding the actual structure, which basically contains all the possible conformers. Considering the ethane molecule, for example, the sigma bond (σ) between the two sp3-hybridized carbon atoms is considered to be cylindrically symmetrical about a line joining both nuclei, and the bond strength is also expected to be same in all different arrangements.
The molecule can perform a free change of conformation from one to another only if the energy of different arrangements is the same or similar. However, considering certain physical properties, it has been observed that the rotation about the carbon–carbon sigma bond is monitored by an energy barrier (about 3 kcal/mole for ethane), giving evidence that the potential energy of a molecule changes in different conformations. One of the most widely used methods for the representation of structural conformers is called Newman projection, which is named after its developer, M.S. Newman.
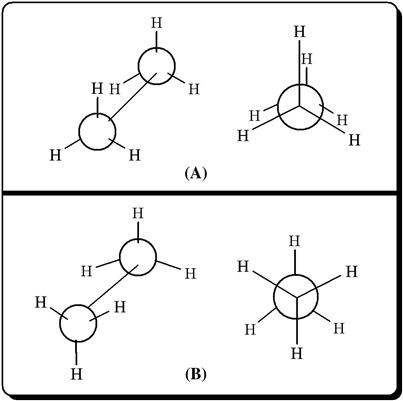
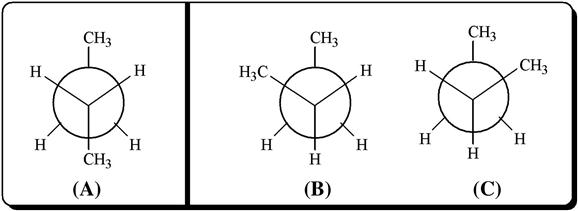
In Figure 5.3, two different conformers of ethane are shown, in which the form a is termed staggered conformation, while the name of representation b is known as eclipsed conformation. In between these two, an infinite number of conformations can theoretically exist, which are called skew conformations. The staggered conformation is characterized by minimal potential energy (hence more stability for a given molecule); the energy rises following free rotation and reaches a maximal value at the eclipsed conformation. The energy required for conversion from one conformer to another is defined as torsional energy, and relative instability of any conformation is depicted in terms of torsional strain. It may be noted that a molecule in the eclipsed conformation faces instability owing to other forces besides torsional strain. These include van der Waals force, dipole–dipole interaction, and hydrogen bonding contributed by neighboring atoms or groups (this does not apply in the case of ethane). We would like to elaborate this point with one additional example, concerning n-butane. Unlike ethane, n-butane contains two terminal methyl groups attached to each of the carbon atoms number 2 and 3. As a result, n-butane is characterized by three staggered conformations (Figure 5.4). Here, the arrangement i is termed anti, as both the methyl substituents are placed farthest apart, while the rest two conformers are named gauche, where the substituent methyl groups are close to each other. The anti conformer has been observed to be more stable because of the absence of the steric van der Waals repulsion caused by the closely placed methyl groups of the gauche form [3]. Note that the energy required for interconversion of various conformers in case of ethane or butane is easily supplied from the collisions among the molecules at room temperature, and the individual conformers cannot be isolated.
The behavioral manifestation of chemicals has long been observed to depend upon a suitable molecular arrangement in 3D space; hence conformation is considered to play an important role in modulating the activity/property/toxicity of chemicals. Barton [4] is considered as one of the pioneering contributors to the exploration of conformational analysis about the search for most reactive species. Barton defined conformational analysis as the nonsuperimposable arrangements of the atoms of a molecule in space and is known for depicting the impact of equatorial and axial orientation of substituents in monitoring the reactivity of substituted cyclohexanes. Hence, conformational analysis is aimed in finding out the energetically stable form; that is, the minimum energy structures or conformers of a molecule. The principal objective of conformational analysis is to gather data about the conformational features of flexible bioactive molecules (including drugs) and then assessing the correlation of the conformational flexibility with the activity of the analyzed molecules. Therefore, conformational analysis plays a pivotal role in various computational chemistry operations like molecular docking, library screening, and the optimization and design of lead molecules.
5.3.2 Conformational search
Conformational analysis involves a search for the identification of suitable molecular conformers that define the actual behavior of the molecule and are present at minimum points at the energy surface. The identification of a low-energy conformer of a molecule can be achieved by employing different search algorithms, which involve systemic variation of torsion angle, stochastic variation of torsion angle, stochastic variation of Cartesian coordinates, stochastic variation of internuclear distances and methods, which use molecular dynamics (MD); and the flipping, flapping, and flexing of rings or mapping of the rings onto generic shapes. [5]. Table 5.1 gives a representative overview of various “search” methods [6] usually employed for the purpose of conformational analysis, while different experimental techniques (noncomputational) used to characterize conformational analysis [7] are briefly presented in Table 5.2.
Table 5.1
An overview of different conformational search methods
| Sl. No. | Name of the search method | Brief description |
| 1 | Systematic search | Grid search: |
| Considering a dihedral angle to be the dominating parameter for differentiating conformers, conformers are generated by systematically varying the dihedral angle by some increment while keeping bond angle and length fixed, thereby obtaining all combinatorial possibilities of dihedral angles for the molecule. This type of systemic searching of conformers, termed as grid search or grid scan, generates an intractable number of conformers without identifying the unique low-energy local minima on the conformational hypersurface. | ||
| Custom search: | ||
| Here, specific values are assigned to the torsion angles. Such approach is advantageous if favorable states of torsion angles are known from a previous knowledge (study) so that one can limit the systemic search. Furthermore, this method can operate simultaneous changes in several torsion angles. | ||
| 2 | Model-building method | This method uses molecular fragments or larger building blocks, considering each fragment to be independent of the other. Hence, it is a substructure-based method and is applicable to molecules in which fragments are available. |
| 3 | Random approach | Following the generation of an initial structure, a random movement in Cartesian space occurs, leading to minimization. This minimized conformer is added to a list, the operation moves to the next starting structure, and the method stops after obtaining desired structures or completion of sampling of all conformers or the finish of a predefined number of steps. |
| 4 | Distance geometry | In this method, a matrix of all pairwise atomic distance values in a molecule is used to form a series of Cartesian coordinates. Standard geometries are used for some of the distances, while the others are gathered from experimental data and random number generation, as provided by the upper- and lower-bound range of the known distance. This method is suitable for the search of both small molecules and macromolecules. |
| 5 | Monte Carlo method | Here, simulation of the dynamic behavior of a molecule is done by randomly making changes to the system like rotation of dihedral angles or displacement of atoms. The newly generated atomic configuration is accepted if its energy is less than the previous one. However, in the case of a higher energy value of the conformer, acceptance is made using an algorithmic probability, such as the Metropolis algorithm. The probability is defined by the Boltzmann distribution as follows: 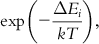 where k is the Boltzmann constant and T is the absolute temperature. If a randomly generated number is smaller than the Boltzmann factor, the configuration is accepted. where k is the Boltzmann constant and T is the absolute temperature. If a randomly generated number is smaller than the Boltzmann factor, the configuration is accepted. |
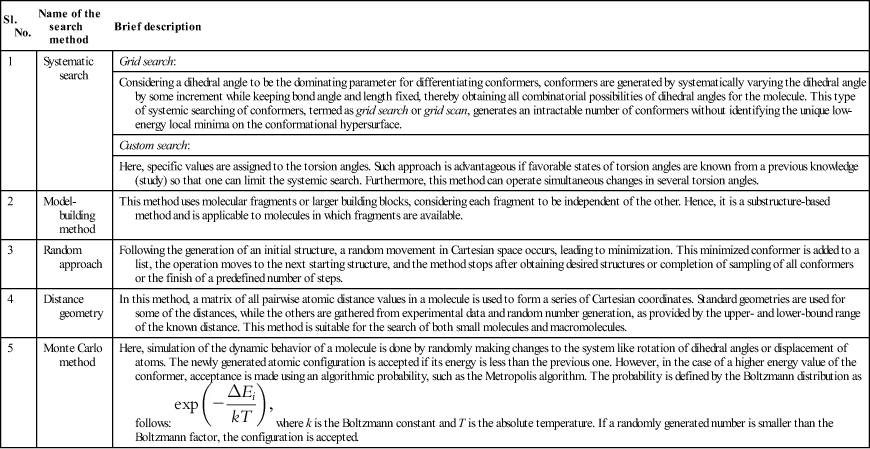
Table 5.2
Some representative experimental methods employed for characterizing conformational analysis
| Sl. No. | Experimental techniques for conformational analysis | Brief notes |
| 1 | Gas-phase electron diffraction (GED) | A powerful old technique. Limitation includes interpretation of the experimental data. GED has been used by the researchers for the conformational analysis of ethane, cyclohexane, chlorocyclohexane, etc. |
| 2 | Electronic circular dichroism (ECD) | A chirooptical method. Useful in analyzing conformers that are different in the relative character of the chromophoric parts, giving different ECD spectra. |
| 3 | Vibrational circular dichroism (VCD) | Uses the infrared (IR) technique and is more advantageous than ECD since conformational changes are more sensibly reflected by IR bands and it does not necessitate chromophoric groups. |
| 4 | Raman optical activity (ROA) | Rarely used. Studies have been carried out on chiral deuterated [2H1, 2H2, 2H3]-neopentane. |
| 5 | Dynamic nuclear magnetic resonance (DNMR) | Allows wide signal dispersion and high sensitivity of chemical shifts toward conformational change. Can be operated at different NMR frequencies (e.g., 1H, 19F, 13C, 29Si, 31P), as well as in a wide temperature range. |
| 6 | Nuclear overhauser effect (NOE) | Proton–proton intramolecular NOE determines the H-atoms in a molecule that are reciprocally close. It has been employed for determining stereochemical features of taxane derivatives. |
5.3.3 Minimization of energy
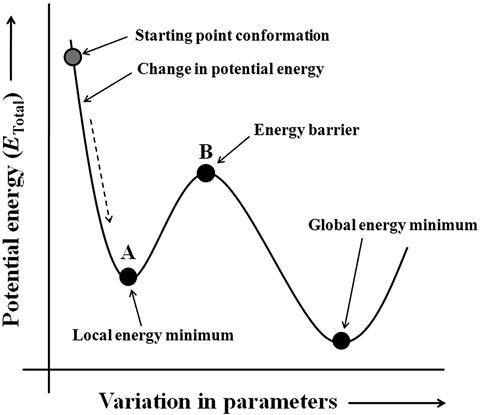
Energy minimization is essential to determining the proper molecular arrangement in space since the drawn chemical structures are not energetically favorable. The potential energy of a molecule contains different energy components like stretching, bending, and torsion; hence, when an energy minimization program is run, it will immediately reach a minimum local energy value, and it might stop if the employed program is not exhaustive. In other words, an energy minimization might stop after it finds the first stable conformer that is structurally closest to the starting molecular arrangement. At this point, identified as the local energy minimum, structural variation yields a low change of energy; hence, minimization can stop. However, this may not be (and usually is not) the most stable conformer since the structural minimization stops before an energy barrier. This encumber of energy can be overcome by the use of suitable algorithms, which can increase the strain energy of the structure and finally lead to the most stable conformer, called global energy minimum. Hence, the identification of the energy minima (i.e., the potential energy hypersurface of a stable molecule) is crucial to determining its behavior. Molecular modeling operation (namely, MD) allows achieving the most stable conformational stage. Figure 5.5 shows different possible phases of an energy minimization operation. Now, since we are interested in finding the behavior of bioactive molecules, our intention will be finding the bioactive conformer. Although the most active conformer seems to be biologically potent, studies have shown that the bioactive conformer might differ from it. However, the bioactive conformer remains in a zone close to the most active conformer. Usually, if the cocrystal geometry of a molecule is present (i.e., geometry a ligand bound to a receptor pocket determined by experimental study like X-ray crystallographic analysis), that conformation of the ligand is considered as the bioactive molecular arrangement or conformation. In the absence of any cocrystal geometric structure, one can consider the most stable conformer as the bioactive conformer. It might be interesting to note that various studies have focused on the determination of the global energy minimum even if the cocrystal geometry of the molecule is present, thereby allowing a comparative assessment of molecular geometry.
The energy minimization methodology needs to involve identification of the point closest to the starting structure. It might involve a separate algorithmic support for the generation of initial starting structures toward ensuing minimization. It is necessary to understand the difference between conformation searches and other simulation operations like MD and Monte Carlo simulation. Conformational analysis aims to identify minimum energy structures, while simulation operations give an assembly of states that includes structures not at energy minima. However, both MD and Monte Carlo methods can be deployed as part of the conformational search mechanism. Therefore, minimization of energy of 3D structures is crucial to identifying the molecular behavior, but the level of analysis purely depends on the employed algorithm.
Two most important methods facilitating the computational aspects of theoretical chemistry are calculations involving MM and quantum mechanics. The approaches are directed toward the development of energy equations for the total structure of a molecule under investigation. One of the important aspects of these analyses is the position of the atoms in a molecular structure, which is defined by Cartesian or polar coordinates. The initial values of the coordinates can either be set by the modeler or can be obtained from preexisting structural fragments where computer programs set up the coordinates from the program database. Computer programs also can adjust the coordinates if additional fragments are added considering their relative positions. After running a job of MM or quantum mechanics (i.e., the establishment of an energy equation), a final set of coordinates for the minimized structure is calculated by computer. This final coordinate set is converted by using a suitable graphics package for the visualization of the energy-minimized structure. Figure 5.6 presents arbitrary Cartesian and polar coordinates in a 3D plane. Now, it should be noted that although calculations made using computer programs are likely to yield precise results, the conditions or constraints at which computations are made need to be considered. In many cases, the default calculations are based on a molecule defined at 0 K in vacuum instead of considering the actual influences of molecular vibration or the effects of the medium. Quantum mechanical calculations consume considerably more computation power than molecular mechanical calculations [8]. The choice of method depends upon the desire of the modeler and (more often) the available information.
5.4 Molecular Mechanics
MM assumes that the relative positions of the nuclei of the atoms forming a structure are a function of operating attractive and repulsive forces [9]. Different types of bond stretching, angle bending, torsional energy, and other nonbonded attributes are computed by employing equations of classical physics, giving various interactions and energies also known as force fields. Thus, the total potential energy of a molecule is expressed as the sum of all different types of attractive and repulsive forces between the atoms in the structure, considering the impact of nuclei and avoiding the impact of electrons. A hypothetical mechanical model is employed that considers spheres joined by mechanical springs, where the sphere and spring represent the atom and covalent bond, respectively, thereby allowing the application of laws of classical mechanics. A general form of the equation showing components of the total energy can be represented as follows:
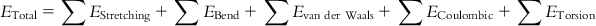 (5.1)
(5.1) It is beyond the scope of this chapter to provide detailed discussions on all different energy terminologies. A brief explanation on the force and energy terminologies presented in Eq. (5.1) has been provided in Table 5.3.
Table 5.3
Formal definition of different energy terms that define the total energy of a molecule
| Phenomenon | Equation | Brief explanation |
| Torsion | 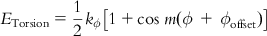 | Torsional energy presents the energy required for the free rotation of a sigma bond. Torsion is about the atoms that are separated by three bonds from each other. The torsion angle represents the dihedral angle defining the relative orientation of the atoms. The following figure shows the torsion angle ϕ between two sample atoms in a staggered conformation.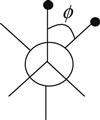 |
| where ϕoffset is the ideal torsion angle relative to a staggered conformation of two atoms and kϕ represents the energy barrier for rotation about the torsion angle ϕ. The periodicity of rotation is denoted by m. | ||
| Bond stretching | 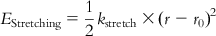 | Considering a covalent bond made up of a spring, Hooke’s law can be employed for the computation of bond stretching energy. However, the Morse function containing complex mathematical terms also allows computation of bond stretching. |
| where the ideal and stretched bond lengths are denoted by r0 and r, respectively, and kstretch is a force constant giving a measure of the strength of the spring; that is, the bond. Hence, a double bond will have a larger value of kstretch than a single bond. | ||
| Angle bending | 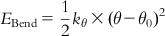 | The ideal bond angle corresponds to the angle formed by three consecutive atoms at their minimum energy position. Bending angle θ can be represented as follows, where the arrows show movement of atoms: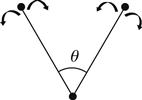 |
| where the ideal bond angle is denoted by θ0 and θ is the bond angle in the bending position. | ||
| van der Waals force | 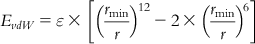 | The van der Waals force of interaction can be represented by the Lennard–Jones potential equation, where the first term bearing power 6 {()6} represents forces of attraction, and the term with 12th power {()12} denotes the short-range repulsive forces involved. |
| Here, at minimum energy value ε, rmin presents the distance between atoms i and j while the actual distance between the atoms is r. | ||
| Coulombic force | 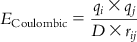 | Measures the effect of a charge between two points. The attractive or repulsive interaction between two atoms i and j separated by distance rij can be represented as 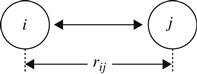 |
| where qi and qj represent the point charges on atoms i and j, respectively, with rij being the distance between them. D denotes the dielectric constant of the medium. |
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree