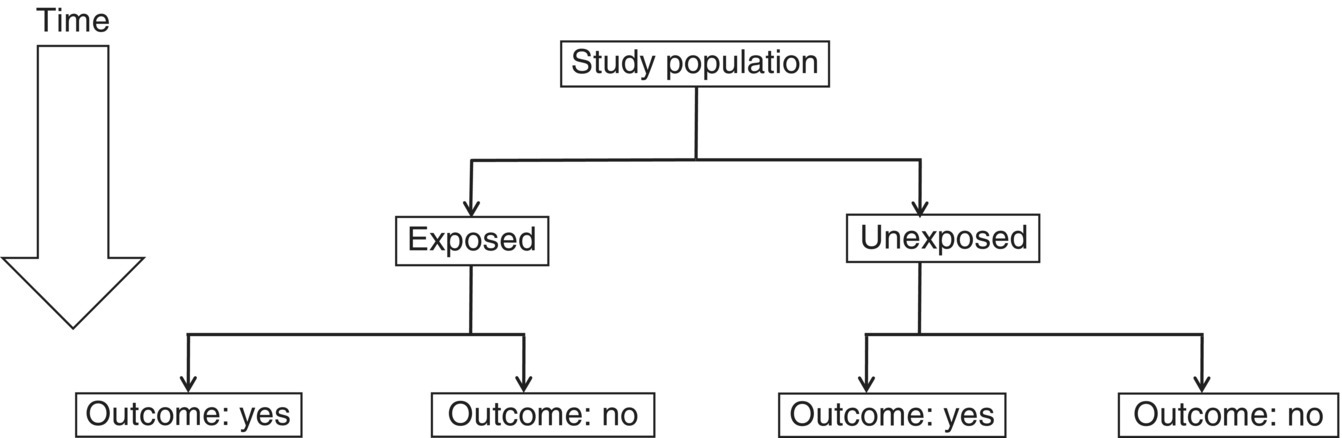
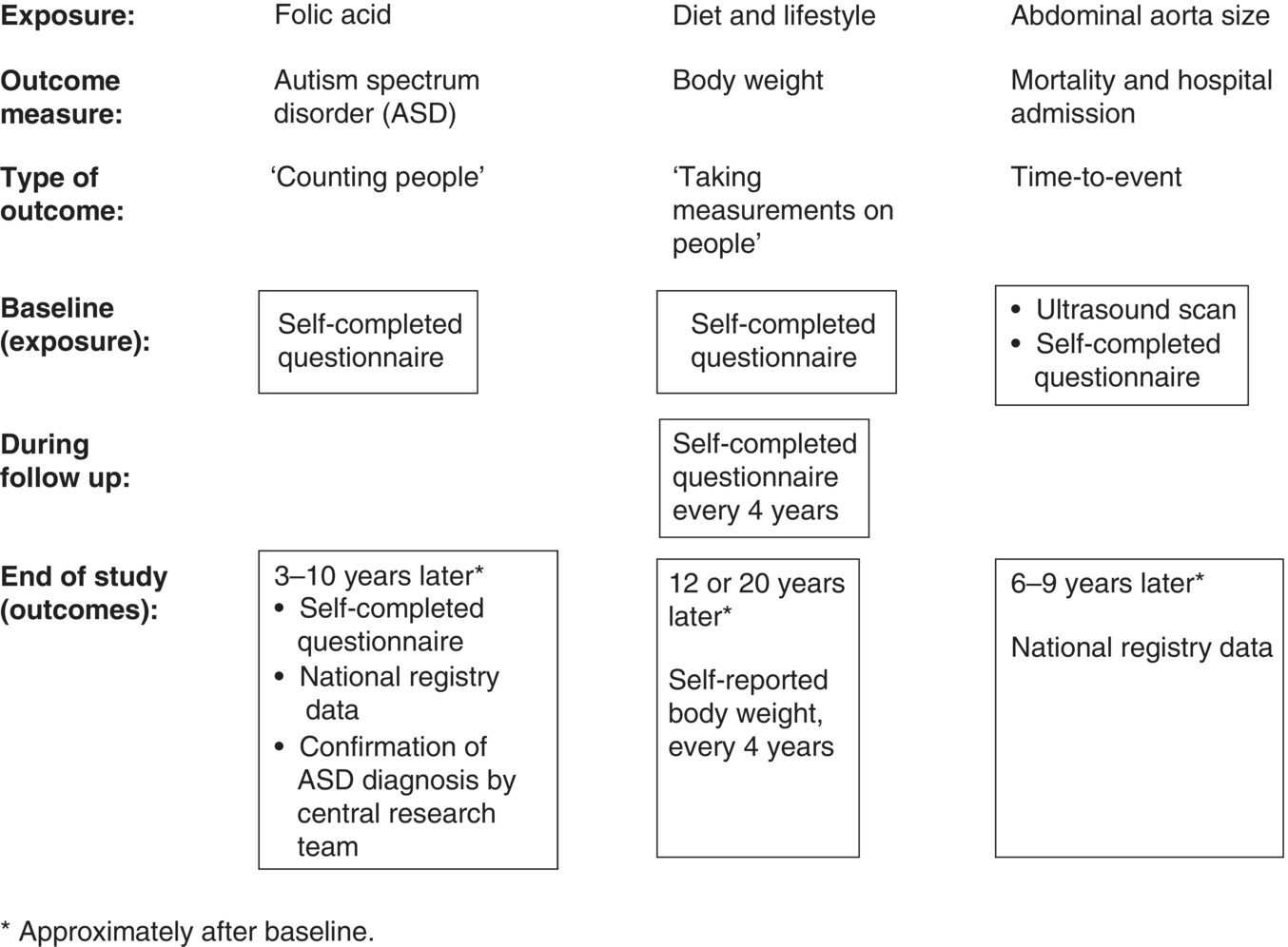
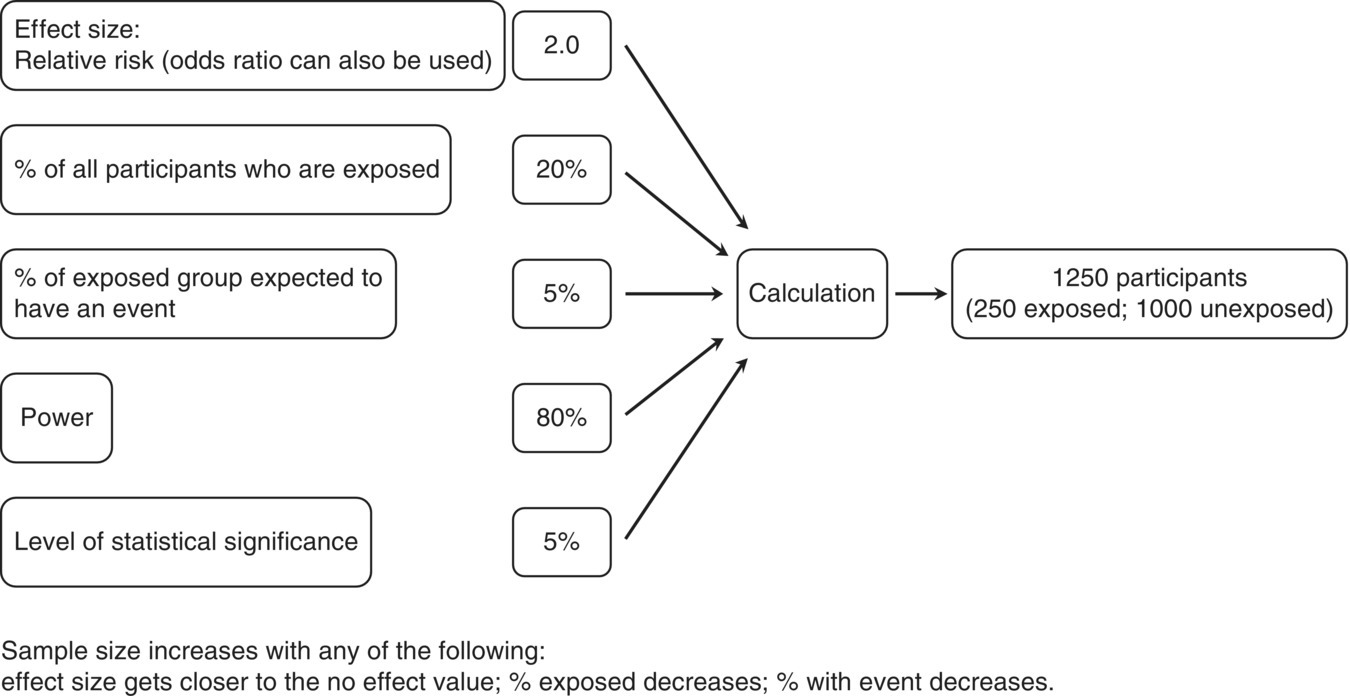
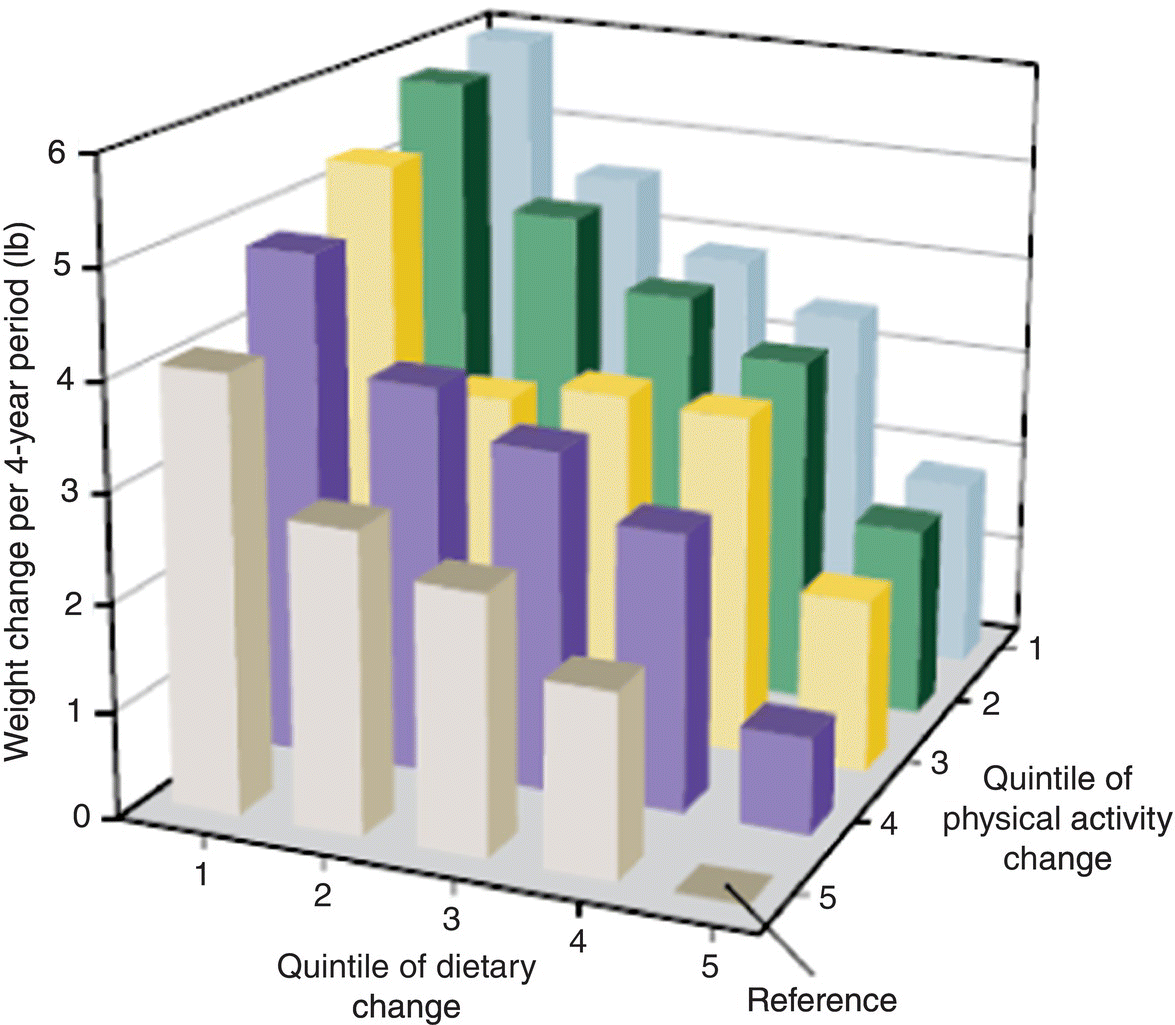
Chapter 7 Cohort studies are generally considered to be the best type of observational study for evaluating risk factors and causality, and sometimes the natural history of a disorder. Such studies may also be useful in evaluating treatments with large effects, although there may still be uncertainty over the actual size of the effect (if confounding and bias are not adequately allowed for). More details about cohort studies can be found elsewhere [1–4]. The key difference between a cohort study and the other types of observational studies (i.e. cross-sectional and case–control) is the prospective collection of data. This may occur, to a small extent, in cross-sectional studies, such as in the example in Box 5.5 in which study participants recorded dietary data over a week, but for a cohort study, data need to be collected over a much longer time period (usually months, sometimes years). The ultimate purpose is usually to observe new events (e.g. new cases of a specific disorder, changes in habits or lifestyles, or deaths) or how measurements change over time. Figure 7.1 shows the general design of a cohort study. Figure 7.1 General design of a cohort study. A common definition of a typical prospective cohort study is that it is based only on people without the disorder of interest at baseline. For example, if examining the association between smoking and cancer, only people free from cancer would be eligible for the study. The participants might be described as ‘healthy’ individuals, although technically this would be incorrect, because some are likely to have other disorders.1 However, several cohort studies do not focus on a single disorder when asking people to participate. Instead, the statistical analysis of a particular disorder is performed, after those who have (or have had) it at baseline are excluded. There are two types of cohort studies: prospective and retrospective. A prospective cohort study involves recruiting participants in the present time, finding information about them now (or about their past), and then obtaining new data on them in the future. A retrospective (or historical) cohort study sounds like a contradiction in terms, but it can be thought of as a prospective cohort that has already taken place. Participants are identified from existing records, including information about their characteristics, habits, and exposures, and then data on outcomes over a specified time period, perhaps up to the present day, are examined. The obvious disadvantage of a retrospective cohort study is that only data that have already been collected can be used, so there is the potential for missing data, whereas in a prospective cohort study, the researchers can request the data they need and missing data can be minimised. A major advantage of a retrospective cohort study is that it can be performed much more quickly, because there is no requirement to wait several months or years to collect information on the outcome measures. Such studies are also often used to examine biological markers using stored samples (e.g. from biobanks associated with the study). Prospective cohort studies are less easy to conduct than retrospective studies, because of the fundamental feature of regular contact with the study participants, either directly or indirectly, over several months or years. Many cohort studies, particularly those that are based on many participants from a relatively wide geographical location (e.g. nationally) do not have a single specific research objective. This is essentially to maximise the usefulness of the study, given the resources (staff and money) they require to set up and conduct. There may be research questions that only arise during the subsequent years, that were not apparent at the start of the study. Examples of well-known cohort studies are the British Doctors Study (established in 1951) [5] and the US Cancer Prevention Studies (I and II, which started in 1959 and 1982, respectively) [6]. All three have reported on a range of disorders over several decades, including different types of cancers, and cardiovascular disease. Cohort studies could have a fixed accrual period, where participants are only asked to take part between certain dates (e.g. January–December 2005), or may be dynamic, in that people could take part any time. The fixed accrual period is most common, but dynamic accrual might be appropriate for studies based on, for example, hospital patients, in which it is easy to add to the cohort, and to follow them up. As with all observational studies, a sampling frame must be used, and this should be representative of the target population of interest. Box 7.1 shows the sampling frames for three examples, covered in this chapter [7–9]. Boxes 7.2 to 7.4 illustrate key features of the examples, to highlight cohort studies in general. When the exposed and unexposed participants are found within the same study population (i.e. sampling frame), this can be referred to as an internal comparison. However, it may be difficult to find a sufficient number of unexposed individuals in the cohort of interest. For example, if the research question is to examine the effect of coal dust on the risk of lung cancer among coal miners, all would be exposed. Therefore, an unexposed group must be found elsewhere, using a separate sampling frame, such as the general population, or perhaps another occupation. This can be referred to as an external comparison. It is important to avoid choosing an unexposed group that could lead to bias, which would under- or overestimate the association. Once the sampling frame is identified, there may be no specific eligibility criteria. This was the case in the example on folic acid, in which all maternity units with >100 births annually were included, and all pregnant women who attended for the routine ultrasound examination were asked to take part. If eligibility criteria are to be applied, this may be done in two ways: at the start, when approaching participants, or for the analysis associated with a specific research objective. In the example of lifestyle habits (Box 7.3) and abdominal aorta size (Box 7.4), age at baseline was an inclusion criterion, so only people within a certain age range were invited to participate (Box 7.1). However, additional criteria were applied to the study of lifestyle habits when selecting the data for the analyses (i.e. after follow-up), in which people who had certain existing disorders at baseline were excluded (Box 7.3). If investigating causality, a key strength of cohort studies is ensuring that an exposure came before the disorder of interest (Box 2.6). There is no reason to recruit or analyse people who already had the disorder at baseline. In the three examples in this chapter, the outcome measures were children with ASD (Box 7.2), change in body weight (Box 7.3), or death/hospital admission (Box 7.4). In the first and third examples, it is clear that the exposures came (and were measured) before the outcomes. In the second example, the change in body weight was recorded at the same time as changes in diet, when each could be compared with the baseline values. In a cohort study, exposures and other factors are measured at baseline, and outcome measures are ascertained over the subsequent months or years. The most common type of cohort study analysis is of the association between the baseline information and the outcomes. However, some exposures, for example, diet and lifestyle (Box 7.3), could change over time, especially if there is a long follow-up period. If this is likely to occur, the exposures should be measured during follow-up (called longitudinal cohort study). Interest would be in how changes in diet and lifestyle over time influence the outcome measures (such as cardiovascular disease). Figure 10.1 is an example in which using only baseline exposure information could lead to a diluted effect if the exposure status significantly changes during a long follow-up period. Principles covered in Section 5.3 also apply to cohort studies. Cohort studies are commonly used to estimate risk, that is, the chance of having a defined event (e.g. stopped smoking), of developing a specific disorder, or of death. Studies of risk such as these could use two types of outcome measures: ‘counting people’ and time-to-event data. However, there are also cohort studies that aim to examine how certain outcomes change over time (e.g. measures of blood pressure or body weight), and for these, there is no concept of risk.2 Exposures and outcome measures should be measured using the same methods for all participants, and when determining the outcome measure, it is best to use standard and validated criteria where possible. An established method for cause of death is the World Health Organisation ICD. Non-standard methods developed specifically for a study require careful explanation and justification, and if the method has been developed and then tested on the same dataset, there is a possibility of bias. Independent assessment of the outcome measure for all individuals may strengthen the reliability of the findings, that is, assessment by someone who does not know the exposure status of the participant or is not directly involved in the research study team (but this can be expensive to do). Data for cohort studies can be collected in a similar way to case–control studies (Section 6.4) or cross-sectional studies (Section 5.4). Unlike some case–control and cross-sectional studies, in which a proxy could provide data for the study instead of the participant, it is usual for cohort studies to obtain information directly from the participants (particularly the baseline information). The three examples in this chapter show that data were collected in a variety of ways (Figure 7.2). Prospective cohort studies require significant resources, so efficient methods are needed to capture data, especially during follow-up which can last for several years. Attempting to collect data regularly requires a balance of objectives: Figure 7.2 How data were collected in the three cohort studies used as examples in this chapter. ‘National registry data’ do not directly involve the study participant. Self-completed questionnaires during follow-up are an efficient way of requesting large amounts of information but non-responders and incomplete responders are likely. Telephone surveys, where the researcher works through the questionnaire items with the study participant, could overcome this, but these require staff (increasing costs) and often a shorter questionnaire, because participants are unlikely to want to spend much more than an hour going through a survey by telephone. In the future, cohort studies are likely to involve more information technology (see page 19). There are two major problems with prospective cohort studies, which often increase with longer follow-up and can have an impact on the study size available for the statistical analyses and therefore reliability of the results: These two features are different. Obtaining outcome measures on those lost to follow-up is usually impossible, but this is not necessarily the case for those who withdraw. The three examples used in this chapter are each based on many study participants. Although it is possible to conduct relatively smaller studies, for example, from a single centre in which there may only be 100 individuals to follow up, the size and duration of follow-up must still be sufficient to address the study objectives. Many cohort studies are already ongoing, with fixed numbers of participants and events, so a sample size calculation for a specific research objective might have limited value or not done, as in two examples covered in this chapter [8,9]. However, if a sample size were estimated, and the target number of participants and/or events far exceeded that observed in the study, the researchers may still wish to proceed with the analysis. The principles of sample size estimation for cohort studies are similar to those for case–control studies (see Section 6.5). When the outcome measure is based on ‘counting people’ or time-to-event data, the number of events is important, often more so than the total number of participants in the study. Therefore, although it might be easy to conduct a small cohort study, finding no or few events would not provide useful information (wide 95% confidence intervals and large p-values). If the number of participants recruited is limited, extending the follow-up may increase the number of events. There is, therefore, a relationship between target sample size, expected event rate, length of follow-up, and available resources that need to be considered by researchers. When there is a single exposure factor of interest and a single outcome measure (e.g. disorder), several pieces of information are needed for the sample size calculation (Figure 7.3). Items such as the percentage of participants who are expected to be exposed and the percentage of the unexposed group who would have the outcome should ideally come from prior information but other times are simply best guesses. Statistical packages have sample size facilities, and there are software programmes [10, 11], including those freely available for observational studies [12]. Figure 7.3 Information required for a sample size estimation for cohort studies in which the effect size is a relative risk. For example, in the folic acid study, Box 7.2, the study size of 85,176 had 93, 73 and 45% power to detect odds ratios of 0.50, 0.60 and 0.70 respectively, assuming 68% of the participants were exposed (ie. mothers took folic acid) and ASD prevalence of 0.13%. Drop outs could be allowed for in the sample size. For example, if the calculation produced a study size of 1000 participants and 15% are expected to be lost during follow-up (there is no measure of the endpoint on them), the target size could be inflated to 1180 [85% of 1180 is 1000, where 1180 = 1000/(1 − 0.15)]. When the outcome measure is based on ‘counting people’ or time-to-events, the concept of risk is used. Unlike cross-sectional or case–control studies, cohort studies can be used to estimate the incidence of a disorder. When considering the influence of potential confounding factors, the same approaches are used as covered in Chapter 6 (including Figure 6.3). In most studies, the participant is obvious and is almost always a single individual. However, in this example, the ‘participant’ was a mother/child pair. The mother was recruited and provided exposure information, but the outcome measure was obtained on the child, during follow-up. It is possible that a woman could have had more than one pregnancy during the recruitment period of 2002–2008 and so be counted more than once. The original study aimed to examine several factors associated with the mothers and outcome of pregnancy (the child and mother), so there was no single research objective. But the exposure of interest in this particular analysis was folic acid supplementation. Women were recruited to the study at 18 weeks of pregnancy, but the survey given at the time requested details about folic acid intake as far back as 4 weeks before the start of pregnancy, requiring them to remember their intake over the past 5–6 months, including intake in each 4-week interval up to 18 weeks. It is possible that many women were still continuing supplementation to 18 weeks, making it easier to recall this information accurately. To simplify matters, women were only asked whether or not they took folic acid, rather than the amount taken. Recall bias (Box 1.6) would not occur in this situation, because women had not yet given birth, so there should not be a differential report in folic acid use between those with children with ASD and those who were unaffected. The outcome measure of interest was the diagnosis of ASD, of which there were three types: autistic disorder, Asperger syndrome, and ‘pervasive developmental disorder not otherwise specified’. Children suspected to have ASD were initially identified using the questionnaires sent to mothers during follow-up, or from a national hospital registry (to which the study participants could be linked), which indicated that the child had already been diagnosed with ASD. The child was then invited for a clinical assessment, and ASD was diagnosed or confirmed using standard and validated criteria, based on the evaluation as well as information from parents and teachers. This approach attempted to maximise the number of affected individuals assessed in the same way, and it used an independent assessment of ASD diagnosis. Importantly, the clinical assessment was conducted without knowledge of the exposure status of the mother/child. The outcome measure (chance of having a child with ASD) was analysed using a logistic regression (see page 69). Published results should usually include a table showing the study participants by baseline characteristics and according to exposure status (if appropriate).3 There are two reasons for this: In this study, there were clear baseline differences between the exposed and unexposed groups: The main results are shown in Table 7.1. The investigators analysed each type of ASD separately; it is always useful to show both the number of study participants and number of events in each exposure group. The effect size for this type of outcome measure is the odds ratio (OR). Although researchers can calculate relative risks from cohort studies, this study was analysed using logistic regression because confounding factors can be adjusted for. Logistic regression analysis works with OR, which can usually be interpreted in a similar way to relative risks, unless the disorder is common (see Table 3.2). In this study, the unadjusted OR was 0.51 (49% risk reduction), indicating a halving of the risk of having a child with autistic disorder among women who took folic acid, compared with those who did not. This is a large effect. The adjusted OR becomes 0.61 (39% risk reduction), and still represents a clinically important effect. The potential confounding factors had only relatively small effect on the association between folic acid use and risk of autistic disorder. Reporting both the unadjusted and adjusted effect sizes is useful, in order to demonstrate the influence of potential confounders. The results for Asperger syndrome suggested a decreased risk by 35% (OR 0.65). Table 7.1 also shows the OR according to when women started to take folic acid (i.e. whether the ORs decreased or increased). It is plausible that women who took folic acid for the longest would have had the greatest reduction in risk, but there was no such obvious trend here. However, a major problem with this analysis is that each subgroup was based on relatively few events, so there was no clear pattern. The 95% CI for autistic disorder was 0.41–0.90 (Table 7.1). The true OR is likely to be somewhere between 0.41 (59% reduction) and 0.90 (10% reduction), and the best estimate was 0.61 (39% risk reduction). The CI is quite wide, considering the large study size; however, the width is determined by the standard error, which is influenced by both study size and number of events ( Box 3.8). In this example, there were 85,176 participants (mother/child pairs), but the number of autistic disorder cases (events), 114, was relatively small. Nevertheless, the results are sufficiently reliable to make a conclusion. For Asperger syndrome, the 95% CI was also quite wide (0.36–1.16), but this is again unsurprising, given the relatively low number of cases (48). The interval includes the no effect value, so there is a possibility that the true OR for this group was 1.0. No p-values were reported in the published paper, but because the 95% CI excludes the no effect value (OR of 1.0), the p-value must be <0.05 (Figure 3.7). The observed OR of 0.61 is unlikely to be due to chance and is probably a real effect. In addition, the upper limit (0.90) is relatively far from the no effect value, so the p-value is likely to be fairly small. Using Box 6.8 the estimated p-value is 0.01. The adjusted OR indicated a moderate/large effect, and design strengths of the study included the large number of participants, prospective collection of outcome measures, and a combination of methods to ascertain ASD. The authors considered some limitations: There was independent evidence from a case–control study that found a lower risk of ASD among women who took prenatal folic acid, and there was already established biological evidence of the beneficial effect of this vitamin on neural tube development including a randomized clinical trial of folic acid and prevention [13]. Although the authors of the cohort study found an association, they could not establish causality, which is an appropriate conclusion to make. In this example, the main outcome measure was body weight, which represents continuous data, so there is no direct concept of risk. The purpose was to see how these measures changed, over time, as the exposures changed. This is a type of cohort study called a longitudinal study. If the researchers had wanted to examine risk, they would have had to categorise weight, for example, < 100 and ≥100 kg, and the analysis would then have been based on the proportion (risk) of participants who weighed ≥100 kg. Although this approach is easy, information on the variability in body weight is lost in the statistical analysis. There were many exposures, based on specific dietary items and lifestyle habits including daily intake of fruits, vegetables, and alcohol, as well as physical activity, and amount of sleep. Some of these were relatively easy to quantify (e.g. number of hours of sleep per day). However, measuring the dietary items was complex as they are a mixture of solids and liquids, and the amount consumed for each type varied considerably. Using the weight of each item as a measure is impractical, requiring the study participants to weigh (or guess the weight of) the amount of food they consume. The unit of measure chosen for the study was ‘servings per day’. This might appear imprecise, but it indicated what a typical person might consume, in accepted units. For example, a serving of potato chips could be a bag, and a serving of fruit could be an orange. The questionnaires were detailed, but an advantage of using health professionals as study participants is that they would be familiar with the topic, and so may complete the questionnaires more reliably than people from the general population. Body weight was also self-reported by the participants, and measured several times during follow-up (Figure 7.2). A bias could arise if those with the highest weights were more likely to under-report their weight or report a more favourable diet, which could underestimate the association between diet and weight. To determine whether this bias was present, the body weight of a sample of study participants was measured by researchers, and found to be highly correlated with the self-reported weights. In this study the outcome measure, body weight, can be analysed using linear regression (Chapter 3, page 66). Unlike the other two examples in this chapter, in which the exposure was a single, categorical factor, in this study, there were many exposures, so it was not possible to report the baseline characteristics according to exposed and unexposed groups. Instead, the baseline characteristics table in the published paper provides a summary of the key dietary and lifestyle factors in each of the groups used in the paper. Table 7.2 shows the main results for selected exposures (dietary items). Each item is included in the regression as a continuous measure, without being put into categories, and so a linear relationship is assumed between the dietary item and change in body weight. The effect size for each factor (obtained from the linear regression) was the change in body weight over a 4-year period. As expected, there were many potential confounding factors, and each effect size for a dietary item was adjusted for all other items. Allowing for so many factors is usually only reliable for large datasets; in smaller datasets, the regression model could ‘break down’, which could be indicated by very large or small effect sizes or CI limits (may appear as infinity). The results in this study can be assessed by examining whether the effect size materially changes after adjustment, and whether it moves closer or further away from the no effect value (Figure 6.3). The results in Table 7.2 can be interpreted as follows: These changes in weight might appear relatively small, in the context of gains or losses over a 4-year period, but they were associated with only one extra serving, per day, of one food item. Additional servings of the same food item, and the effects of other food/drink items, are therefore likely to have a cumulative effect on weight. It was unexpected that eating more fruit or nuts could lead to weight loss, because both add calories. It is possible that people who ate fruit and nuts reduced their intake of other foods with high calorific content, thus decreasing their total energy intake, which led to the small/moderate weight loss. Figure 7.4 shows the independent effects of diet and physical activity on changes in body weight. Diet was quantified as an overall score, based on changes in each food/drink item. As expected, people with the ‘worst’ diet and the least amount of physical activity had the largest weight gain, on average almost 6 pounds over 4 years, compared with those in the highest category. The figure shows that food consumption and exercise had independent effects. By holding one category of diet constant (so that people had similar diet scores, and therefore diet would not act as a confounder), weight increased with decreasing physical activity (i.e. as the quintile moved from 5 to 1). The same pattern was seen when holding a category of physical activity constant. Figure 7.4 How body weight changes in relation to changes in diet and physical activity. Each food/drink item had a score , and a total score for ‘diet’ was calculated for each participant. A low quintile for diet indicates the 20% of participants who tend to have the ‘worst’ diets (i.e. consume foods or drinks that increase weight), and a low quintile for physical activity indicates the 20% of people who perform the least amount of physical activity. Source: Mozaffarian et al. 2011 [8]. Reproduced by permission of Massachusetts Medical Society.
Cohort studies
7.1 Purpose
7.2 Design
7.3 Measuring variables, exposures, and outcome measures
7.4 Collecting the data
7.5 Sample size
Information needed for sample size estimation when examining associations
7.6 Analysing data and interpreting results
7.7 Outcome measures based on ‘counting people’ endpoints: Folic acid and ASD (Box 7.2)
Measuring variables, exposures, and outcome measures
Analysing data and interpreting results
What are the main results?
What could the true effect be, given that the study was conducted on a sample of people?
Could the observed result be a chance finding in this particular study?
How good is the evidence?
7.8 Outcome measures based on ‘taking measurements on people’ endpoints: Lifestyle habits and body weight (Box 7.3)
Measuring variables, exposures, and outcome measures
Analysing data and interpreting results
What are the main results?
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


