Bioenergetics refers to cellular energy transformations.
The Adenosine Triphosphate–Adenosine Diphosphate (ATP–ADP) Cycle. In cells, the available free energy of fuels is transformed into the physiologic responses that are necessary for life. The central role of the high-energy phosphate bonds of ATP in these processes is summarized in the ATP–ADP cycle (Fig. 20.1). To generate ATP through cellular respiration, fuels are degraded by oxidative reactions that transfer most of their available free energy to nicotinamide adenine dinucleotide (NAD+) and flavin adenine dinucleotide (FAD) to generate the reduced form of these coenzymes, NADH and FAD(2H). When NADH and FAD(2H) are oxidized by O2 in the electron transport chain (ETC), the energy is used to regenerate ATP in the process of oxidative phosphorylation. Energy available from cleavage of the high-energy phosphate bonds of ATP can be used directly for mechanical work (e.g., muscle contraction) or for transport work (e.g., an Na+ gradient generated by Na+, K+-ATPase). It can also be used for biochemical work (energy-requiring chemical reactions), such as anabolic pathways (biosynthesis of large molecules such as proteins) or detoxification reactions. Phosphoryl transfer reactions, protein conformational changes, and the formation of activated intermediates containing high-energy bonds (e.g., uridine diphosphate [UDP]-sugars) facilitate these energy transformations. Energy released from foods that is not used for work against the environment is transformed into heat.

FIGURE 20.1 The ATP–ADP cycle. ADP, adenosine diphosphate; ATP, adenosine triphosphate; Pi, inorganic phosphate.
ATP Homeostasis. Fuel oxidation is regulated to maintain ATP homeostasis (“homeo,” same; “stasis,” state). Regardless of whether the level of cellular fuel utilization is high (with increased ATP consumption) or low (with decreased ATP consumption), the available ATP within the cell is maintained at a constant level by appropriate increases or decreases in the rate of fuel oxidation. Problems in ATP homeostasis and energy balance occur in obesity, hyperthyroidism, and myocardial infarction (MI).
Energy from Fuel Oxidation. Fuel oxidation is exergonic; it releases energy. The maximum quantity of energy released that is available for useful work (e.g., ATP synthesis) is called ΔG0′, the change in Gibbs free energy at pH 7.0 under standard conditions. Fuel oxidation has a negative ΔG0′; that is, the products have a lower available free energy than the reactants and their formation is energetically favored. ATP synthesis from ADP and inorganic phosphate (Pi) is endergonic: It requires energy and has a positive ΔG0′. To proceed in our cells, all pathways must have a negative ΔG0′. How is this accomplished for anabolic pathways such as glycogen synthesis? These metabolic pathways incorporate reactions that expend high-energy bonds to compensate for the energy-requiring steps. Because the ΔG0′ values for a sequence of reactions are additive, the overall pathway becomes energetically favorable.
Fuels are oxidized principally by donating electrons to NAD+ and FAD, which then donate electrons to O2 in the ETC. The caloric value of a fuel is related to its ΔG0′ for transfer of electrons to O2, and its reduction potential, E0′ (a measure of its willingness to donate, or accept, electrons). Because fatty acids are more reduced than carbohydrates, they have a higher caloric value. The high affinity of oxygen for electrons (a high positive reduction potential) drives fuel oxidation forward, with release of energy that can be used for ATP synthesis in oxidative phosphorylation. However, smaller amounts of ATP can be generated without the use of O2 in anaerobic glycolysis.
Fuel oxidation can also generate NADPH, which usually donates electrons to biosynthetic pathways and detoxification reactions. For example, in some reactions catalyzed by oxygenases, NADPH is the electron donor and O2 is the electron acceptor.
THE WAITING ROOM 
 Otto S. is a 26-year-old medical student who has completed his first year of medical school. He is 5 ft 10 in tall and began medical school weighing 154 lb, within his ideal weight range (see Chapter 1). By the time he finished his last examination in his first year, he weighed 187 lb. He had calculated his basal metabolic rate (BMR) at approximately 1,680 kcal and his energy expenditure for physical exercise equal to 30% of his BMR. He planned on returning to his pre–medical school weight in 6 weeks over the summer by eating 576 kcal less each day and playing 7 hours of tennis every day. However, he did a summer internship instead of playing tennis. When he started his second year of medical school, he weighed 210 lb.
Otto S. is a 26-year-old medical student who has completed his first year of medical school. He is 5 ft 10 in tall and began medical school weighing 154 lb, within his ideal weight range (see Chapter 1). By the time he finished his last examination in his first year, he weighed 187 lb. He had calculated his basal metabolic rate (BMR) at approximately 1,680 kcal and his energy expenditure for physical exercise equal to 30% of his BMR. He planned on returning to his pre–medical school weight in 6 weeks over the summer by eating 576 kcal less each day and playing 7 hours of tennis every day. However, he did a summer internship instead of playing tennis. When he started his second year of medical school, he weighed 210 lb.
 Stanley T. is a 26-year-old man who noted heat intolerance, with heavy sweating, heart palpitations, and tremulousness. Over the past 4 months, he has lost weight in spite of a good appetite. He is sleeping poorly and describes himself as feeling “jittery inside.”
Stanley T. is a 26-year-old man who noted heat intolerance, with heavy sweating, heart palpitations, and tremulousness. Over the past 4 months, he has lost weight in spite of a good appetite. He is sleeping poorly and describes himself as feeling “jittery inside.”
On physical examination, his heart rate is rapid (116 beats/minute) and he appears restless and fidgety. His skin feels warm, and he is perspiring profusely. A fine hand tremor is observed as he extends his arms in front of his chest. His thyroid gland appears to be diffusely enlarged and, on palpation, is approximately three times normal size. Thyroid function tests confirm that his thyroid gland is secreting excessive amounts of the thyroid hormones T4 (tetraiodothyronine) and T3 (triiodothyronine), the major thyroid hormones present in the blood.
 Cora N. is a 64-year-old female who had a myocardial infarction (MI; often referred to as a “heart attack”) 8 months ago. Although she has managed to lose 6 lb since the MI, she remains overweight and has not reduced the fat content of her diet adequately. The graded aerobic exercise program she started 5 weeks after her infarction is now followed irregularly, falling far short of the cardiac conditioning intensity prescribed by her cardiologist. She is readmitted to the hospital cardiac care unit (CCU) after experiencing a severe “viselike pressure” in the mid-chest area while cleaning ice from the windshield of her car. The electrocardiogram (ECG) shows evidence of a new anterior wall MI. In addition, signs and symptoms of left ventricular failure are present.
Cora N. is a 64-year-old female who had a myocardial infarction (MI; often referred to as a “heart attack”) 8 months ago. Although she has managed to lose 6 lb since the MI, she remains overweight and has not reduced the fat content of her diet adequately. The graded aerobic exercise program she started 5 weeks after her infarction is now followed irregularly, falling far short of the cardiac conditioning intensity prescribed by her cardiologist. She is readmitted to the hospital cardiac care unit (CCU) after experiencing a severe “viselike pressure” in the mid-chest area while cleaning ice from the windshield of her car. The electrocardiogram (ECG) shows evidence of a new anterior wall MI. In addition, signs and symptoms of left ventricular failure are present.
I. Energy Available to Do Work
The basic principle of the adenosine triphosphate–adenosine diphosphate (ATP–ADP) cycle is that fuel oxidation generates ATP, and hydrolysis of ATP to ADP provides the energy to perform most of the work required in the cell. ATP has, therefore, been called the energy currency of the cells. To keep up with the demand, we must constantly replenish our ATP supply through the use of oxygen (O2) for fuel oxidation.
The amount of energy from ATP cleavage available to do useful work is related to the difference in energy levels between the products and substrates of the reaction and is called the change in Gibbs free energy, ΔG (Δ, difference; G, Gibbs free energy). In cells, the ΔG for energy production from fuel oxidation must be greater than the ΔG of energy-requiring processes, such as protein synthesis and muscle contraction, for life to continue.
A. The High-Energy Phosphate Bonds of ATP
The amount of energy released or required by bond cleavage or formation is determined by the chemical properties of the substrates and products. The bonds between the phosphate groups in ATP are called phosphoanhydride bonds (Fig. 20.2). When these bonds are hydrolyzed, energy is released because the products of the reaction (ADP and phosphate) are more stable, with lower chemical potential energies, than the reactants (ATP and water [H2O]). The instability of the phosphoanhydride bonds arises from their negatively charged oxygen atoms in the phosphate groups, which repel each other and strain the bonds between them. It takes energy to make the phosphate groups stay together. In contrast, there are fewer negative charges in ADP to repel each other. The phosphate group as a free anion is more stable than it is in ATP because of an increase in resonance structures (i.e., the electrons of the oxygen double bond are shared by all the oxygen atoms). As a consequence, ATP hydrolysis is energetically favorable and proceeds with release of energy as heat.

FIGURE 20.2 Hydrolysis of ATP to ADP and inorganic phosphate (Pi). Cleavage of the phosphoanhydride bonds between either the β- and γ-phosphates or between the α- and β-phosphates releases the same amount of energy, approximately 7.3 kcal/mol. However, hydrolysis of the phosphate–adenosine bond (a phosphoester bond) releases less energy (≈3.4 kcal/mol), and consequently, this bond is not considered a high-energy phosphate bond. During ATP hydrolysis, the change in disorder during the reaction is small and so ΔG values at physiologic temperature (37°C) are similar to those at standard temperature (25°C). ΔG is affected by pH, which alters the ionization state of the phosphate groups of ATP and by the intracellular concentration of Mg2+ ions, which bind to the β- and γ-phosphate groups of ATP. ADP, adenosine diphosphate; ATP, adenosine triphosphate.
In the cell, ATP is not hydrolyzed directly. Energy released as heat from ATP hydrolysis cannot be transferred efficiently into energy-requiring processes, such as biosynthetic reactions or maintenance of an ion gradient. Instead, cellular enzymes transfer the phosphate group to a metabolic intermediate or protein that is part of the energy-requiring process (a phosphoryl transfer reaction).
B. Change in Free Energy (ΔG) during a Reaction
How much energy can be obtained from ATP hydrolysis to do the work required in the cell? The maximum amount of useful energy that can be obtained from a reaction is called ΔG—the change in Gibbs free energy. The value of ΔG for a reaction can be influenced by the initial concentration of substrates and products, by temperature, pH, and pressure. The ΔG0 for a reaction refers to the energy change for a reaction starting at 1 M substrate and product concentrations and proceeding to equilibrium (equilibrium, by definition, occurs when there is no change in substrate and product concentrations with time). ΔG0′ is the value for ΔG0 under standard conditions (pH = 7.0, [H2O] = 55 M, and 25°C), as well as standard concentrations (Table 20.1).
TABLE 20.1 Thermodynamic Expressions, Laws, and Constants
| DEFINITIONS | |
| ΔG | Change in free energy, or Gibbs free energy |
| ΔG0 | Standard free-energy change, ΔG starting with 1 M concentrations of substrates and products |
| ΔG0′ | Standard free-energy change at 25°C, pH 7.0 |
| ΔH | Change in enthalpy, or heat content |
| ΔS | Change in entropy, or increase in disorder |
| K′eq | Equilibrium constant at 25°C, pH 7.0, incorporating [H2O] = 55.5 M and [H+] = 10−7 M in the constant |
| ΔE0′ | Change in reduction potential |
| P | Biochemical symbol for a high-energy phosphate bond, i.e., a bond that is hydrolyzed with the release of more than about 7 kcal/mol of heat |
| LAWS OF THERMODYNAMICS | |
| First law of thermodynamics, the conservation of energy: In any physical or chemical change, the total energy of a system, including its surroundings, remains constant. | |
| Second law of thermodynamics: The universe tends toward disorder. In all natural processes, the total entropy of a system always increases. | |
| Constants | |
| Units of ΔG and ΔH = cal/mol or J/mol: 1 cal = 4.18 J | |
| T, absolute temperature: K, Kelvin = 273 + °C (25°C = 298°K) | |
| R, universal gas constant: 1.98 cal/mol-K or 8.31 J/mol-K | |
| F, Faraday constant: F = 23 kcal/mol-Volt or 96,500 J/V-mol | |
| Units of E0′, V | |
| FORMULAS | |
| ΔG = ΔH − TΔS | |
| ΔG0′ = −RT ln Keq′ | |
| ΔG0′ = −n F ΔE0′ | |
| ln = 2.303 log10 | |
ΔG0′ is equivalent to the chemical bond energy of the products minus that of the reactants, corrected for energy that has gone into entropy (an increase in amount of molecular disorder). This correction for change in entropy is very small for most reactions that occur in cells, and thus the ΔG0′ for hydrolysis of various chemical bonds reflects the amount of energy available from that bond.
The value −7.3 kcal/mol (−30.5 kJ/mol) that is generally used for the ΔG0′ of ATP hydrolysis is thus the amount of energy available from hydrolysis of ATP under standard conditions that can be spent on energy-requiring processes; it defines the “monetary value” of our “ATP currency.” Although the difference between cellular conditions (pH 7.3, 37°C) and standard conditions is very small, the difference between cellular concentrations of ATP, ADP, and inorganic phosphate (Pi) and the standard 1 M concentrations is huge and greatly affects the availability of energy in the cell.
C. Exothermic and Endothermic Reactions
The value of ΔG0′ tells you whether the reaction requires or releases energy, the amount of energy involved, and the ratio of products to substrates at equilibrium. The negative value for the ΔG0′ of ATP hydrolysis indicates that, if you begin with equimolar (1 M) concentrations of substrates and products, the reaction proceeds in the forward direction with the release of energy. From initial concentrations of 1 M, the ATP concentration will decrease, and ADP and Pi will increase until equilibrium is reached.
For a reaction in which a substrate S is converted to a product P, the ratio of the product concentration to the substrate concentration at equilibrium is given by:
Table 20.2 indicates a more general form of this equation; R is the gas constant (1.98 cal/mol-°K), and T is equal to the temperature in degrees Kelvin.
TABLE 20.2 A General Expression for ΔG
| To generalize the expression for ΔG, consider a reaction in which |
 |
| The lowercase letters denote that a moles of A will combine with b moles of B to produce c moles of C and d moles of D. |
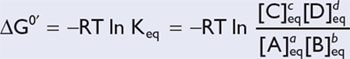 |
| and, when not in equilibrium, |
 |
Thus, the difference in available free energies of the substrate and product (ΔG0′) determines the concentration of each at equilibrium.
Reactions such as ATP hydrolysis are exergonic (release energy) or exothermic (release heat). Both exergonic and exothermic reactions have a negative ΔG0′ and release energy while proceeding in the forward direction to equilibrium. Endergonic, or endothermic, reactions have a positive ΔG0′ for the forward direction (the direction shown), and the backward direction is favored. For example, in the pathway of glycogen synthesis, phosphoglucomutase (PGM) converts glucose 6-phosphate (G6P) to glucose 1-phosphate (G1P). G1P has a higher phosphate bond energy than G6P because the phosphate is on the aldehyde carbon (Fig. 20.3). The ΔG0′ value for the forward direction (G6P → G1P) is therefore positive. Beginning at equimolar concentrations of both compounds, there is a net conversion of G1P back to G6P and, at equilibrium, the concentration of G6P is higher than G1P. The exact ratio is determined by the ΔG0′ for the reaction.

FIGURE 20.3 The PGM reaction. The forward direction (formation of G1P) is involved in converting glucose to glycogen, and the reverse direction in converting glycogen to G6P. G1P, glucose 1-phosphate; G6P, glucose 6-phosphate; PGM, phosphoglucomutase.
It is often said that a reaction with a negative ΔG0′ proceeds spontaneously in the forward direction, meaning that products accumulate at the expense of reactants. However, ΔG0′ is not an indicator of the velocity of the reaction or of the rate at which equilibrium can be reached. In the cell, the velocity of the reaction depends on the efficiency and amount of enzyme available to catalyze the reaction (see Chapter 9), so “spontaneously” in this context can be misleading.
The equations for calculating ΔG are based on the first law of thermodynamics (see Table 20.1). The change in heat that occurs during a reaction is ΔH, the change in enthalpy of the reaction. At constant temperature and pressure, ΔH is equivalent to the available free energy of the products minus that of the reactants. ΔG, the maximum amount of useful work available from a reaction, is equal to ΔH − TΔS. TΔS is a correction for the amount of energy that has gone into an increase in the entropy (disorder in arrangement of molecules) of the system. Thus, ΔG = ΔH − TΔS, where ΔH is the change in enthalpy, T is the temperature of the system in Kelvin, and ΔS is the change in entropy or increased disorder of the system. ΔS is often negligible in reactions such as ATP hydrolysis, in which the numbers of substrates (H2O, ATP) and products (ADP, Pi) are equal and no gas is formed. Under these conditions, the values for ΔG at physiologic temperature (37°C) are similar to those at standard temperature (25°C).
II. Energy Transformations to Do Mechanical and Transport Work
For work in the cell to be done, a mechanism must be available for converting the chemical bond energy of ATP into another form, such as a Na+ gradient across a membrane. These energy transformations usually involve intermediate steps in which ATP is bound to a protein, and cleavage of the bound ATP results in a conformational change of the protein.
A. Mechanical Work
In mechanical work, the high-energy phosphate bond of ATP is converted into movement by changing the conformation of a protein. For example, in contracting muscle fibers, the hydrolysis of ATP while it is bound to myosin ATPase changes the conformation of myosin so that it is in a “cocked” position, ready to associate with the sliding actin filament. Thus, exercising muscle fibers have almost a 100-fold higher rate of ATP utilization and caloric requirements than resting muscle fibers (see Fig. e-20.1 ). Motor proteins, such as kinesins that transport chemicals along fibers, provide another example of mechanical work in a cell.
). Motor proteins, such as kinesins that transport chemicals along fibers, provide another example of mechanical work in a cell.
B. Transport Work
In transport work, called active transport, the high-energy phosphate bond of ATP is used to transport compounds against a concentration gradient (see Chapter 10, Fig. 10.6). In plasma membrane ATPases (P-ATPases) and vesicular ATPases (V-ATPases), the chemical bond energy of ATP is used to reversibly phosphorylate the transport protein and change its conformation. For example, as the Na+, K+-ATPase binds and cleaves ATP, it becomes phosphorylated and changes its conformation to release three Na+ ions to the outside of the cell, thereby building up a higher extracellular than intracellular concentration of Na+. Na+ reenters the cell on co-transport proteins that drive the uptake of amino acids and many other compounds into the cell. Thus, Na+ must be continuously transported back out. The expenditure of ATP for Na+ transport occurs even while we sleep and is estimated to account for 10% to 30% of our BMR.
A large number of other active transporters also convert ATP chemical bond energy into an ion gradient (membrane potential). Vesicular ATPases pump protons into lysosomes. Ca2+-ATPases in the plasma membrane move Ca2+ out of the cell against a concentration gradient. Similar Ca2+-ATPases pump Ca2+ into the lumen of the endoplasmic reticulum and the sarcoplasmic reticulum (in muscle). Thus, a considerable amount of energy is expended in maintaining a low cytoplasmic Ca2+ level.
III. Biochemical Work
The high-energy phosphate bonds of ATP are also used for biochemical work. Biochemical work occurs in anabolic pathways, which are pathways that synthesize large molecules (e.g., DNA, glycogen, triacylglycerols, and proteins) from smaller compounds. Biochemical work also occurs when toxic compounds are converted to nontoxic compounds that can be excreted (e.g., the liver converts NH4+ ions to urea in the urea cycle). In general, formation of chemical bonds between two organic molecules (e.g., C–C bonds in fatty acid synthesis or C–N bonds in protein synthesis) requires energy and is therefore biochemical work. How do our cells get these necessary energy-requiring reactions to occur?
To answer this question, the next sections consider how energy is used to synthesize glycogen from glucose (Fig. 20.4). Glycogen is a storage polysaccharide consisting of glucosyl units linked together through glycosidic bonds. If an anabolic pathway, such as glycogen synthesis, were to have an overall positive ΔG0′, the cell would be full of glucose and intermediates of the pathway but very little glycogen would be formed. To avoid this, cells do biochemical work and spend enough of their ATP currency to give anabolic pathways an overall negative ΔG0′.

FIGURE 20.4 Energetics of glycogen synthesis. Compounds containing high-energy bonds are shown in red. (1) Glucose is transported into the cell. (2) Glucose phosphorylation uses the high-energy phosphate bond (~P) of ATP in a phosphoryl transfer step. (4) Conversion of G6P to G1P by phosphoglucomutase. (5) UDP-glucose pyrophosphorylase cleaves a ~P bond in UTP, releasing pyrophosphate and forming UDP-glucose, an activated intermediate. (6) The pyrophosphate is hydrolyzed, releasing additional energy. (7) The phosphoester bond of UDP-glucose is cleaved during the addition of a glucosyl unit to the end of a glycogen polysaccharide chain. The UDP acts as the leaving group in this reaction. G6P also can be metabolized via glycolysis (3) when energy is required. ADP, adenosine diphosphate; ATP, adenosine triphosphate.; G1P, glucose 1-phosphate; G6P, glucose 6-phosphate; UDP, uridine diphosphate; UTP, uridine triphosphate.
A. Adding ΔG0 Values
Reactions in which chemical bonds are formed between two organic molecules are usually catalyzed by enzymes that transfer energy from cleavage of ATP in a phosphoryl transfer reaction or by enzymes that cleave a high-energy bond in an activated intermediate of the pathway. Because the ΔG0′ values in a reaction sequence are additive, the pathway acquires an overall negative ΔG0′, and the reactions in the pathway will occur to move toward an equilibrium state in which the concentration of final products is greater than that of the initial reactants.
1. Phosphoryl Transfer Reactions
One of the characteristics of Gibbs free energy is that ΔG0 values for consecutive steps or reactions in a sequence can be added together to obtain a single value for the overall process. Thus, the high-energy phosphate bonds of ATP can be used to drive a reaction forward that would otherwise be highly unfavorable energetically. Consider, for example, synthesis of G6P from glucose, the first step in glycolysis and glycogen synthesis (see Fig. 20.4, circle 2). If the reaction were to proceed by addition of inorganic phosphate to glucose, G6P synthesis would have a positive ΔG0′ value of 3.3 kcal/mol (Table 20.3). However, when this reaction is coupled to cleavage of the high-energy ATP bond through a phosphoryl transfer reaction, the ΔG0′ for G6P synthesis acquires a net negative value of −4.0 kcal/mol, which can be calculated from the sum of the two reactions. G6P cannot be transported back out of the cell, and, therefore, the net negative ΔG0′ for G6P synthesis helps the cell to trap glucose for its own metabolic needs.
TABLE 20.3 ΔG0′ for the Transfer of a Phosphate from ATP to Glucose
| Glucose + Pi → glucose 6-P + H2O | ΔG0′ = +3.3 kcal/mol |
| ATP + H2O → ADP + Pi | ΔG0′ = −7.3 kcal/mol |
| Sum: glucose + ATP → glucose 6-P + ADP | ΔG0′ = −4.0 kcal/mol |
ADP, adenosine diphosphate; ATP, adenosine triphosphate.
The net value for synthesis of G6P from glucose and ATP would be the same whether the two reactions are catalyzed by the same enzyme, are catalyzed by two separate enzymes, or are not catalyzed by an enzyme at all, because the net value of G6P synthesis is dictated by the amount of energy in the chemical bonds being broken and formed.
2. Activated Intermediates in Glycogen Synthesis
To synthesize glycogen from glucose, energy is provided by the cleavage of three high-energy phosphate bonds in ATP, uridine triphosphate (UTP), and pyrophosphate (PPi) (see Fig. 20.4, steps 2, 5, and 6). Energy transfer is facilitated by phosphoryl group transfer and by formation of an activated intermediate (uridine diphosphate [UDP]-glucose). Step 4, the conversion of G6P to G1P, has a positive ΔG0′. This step is pulled and pushed in the desired direction by the accumulation of substrate and removal of product in reactions that have a negative ΔG0′ from cleavage of high-energy bonds. In step 5, the UTP high-energy phosphate bond is cleaved to form the activated sugar, UDP-glucose (Fig. 20.5). This reaction is further facilitated by cleavage of the high-energy bond in the pyrophosphate (step 6) that is released in step 5 (approximately −7.7 kcal). In step 7, cleavage of the bond between UDP and glucose in the activated intermediate provides the energy for attaching the glucose moiety to the end of the glycogen molecule (approximately −3.3 kcal). In general, the amount of ATP phosphate bond energy used in an anabolic pathway, or detoxification pathway, must provide the pathway with an overall negative ΔG0′, so that the concentration of products is favored over that of reactants.

FIGURE 20.5 UDP-glucose contains a high-energy pyrophosphate bond, shown in the green box. UDP, uridine diphosphate.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree



