Chapter 6
Case–control studies
6.1 Purpose
Case–control studies are generally considered to be the next most reliable study design after cohort studies when evaluating risk factors and causality (Chapter 1, page 13). Further details on case–control studies can be found elsewhere [1–4].
6.2 Design
Case–control studies specifically involve selecting participants based on a disease or event status (Figure 6.1). They are therefore usually designed with a particular disorder in mind, with participants classified as with or without the disorder (i.e. cases or controls), or to include mortality (dead or alive). However, event status could be used for any defined feature, for example, quit smoking (cases) or not (controls), or leaves hospital within 30 days (cases) or not (controls). Case–control studies are particularly useful when the outcome is relatively rare, making a prospective cohort study unfeasible because there would need to be an impractically large number of participants followed up for a long time before a sufficient number develop the disorder of interest (Box 1.7).
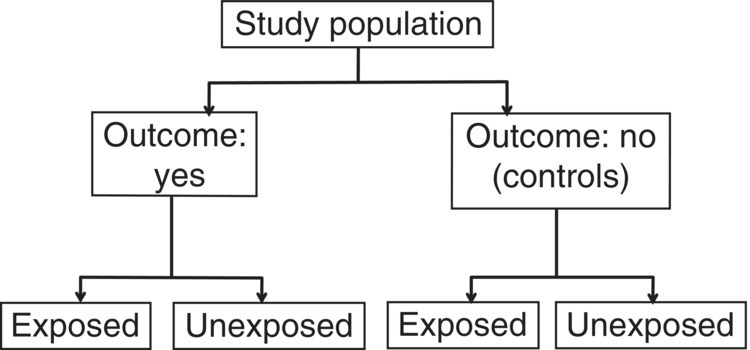
Figure 6.1 General design of a case–control study. ‘Outcome’ could be any pre-defined event, such as a disorder, death, or other characteristic (e.g. did or did not stop smoking).
As with all observational studies, a sampling frame needs to be defined. However, unlike cross-sectional and cohort studies, which usually have a single sampling frame, case–control studies can have two different sources, one for cases and another for controls. Box 6.1 shows three examples, used in this chapter (Boxes 6.2–6.4) [5–7]. The boxes show key features of how the studies were conducted, including exposures and outcomes, and these highlight similar aspects to consider when examining case–control studies in general.
Selecting the cases
Identifying cases can be relatively straightforward, with an obvious sampling frame to work from. They could be found from hospital/clinical records and databases, a network of health researchers, disease registries, notification systems, death certificates, or perhaps found through surveys of the general population. Electronic databases are an efficient method of finding cases because it might also be possible to apply some key eligibility criteria at the outset, before contacting potential participants (saving time).
When considering a disorder, the cases could either be newly diagnosed or have had the disorder for some time; the difference between the two matters when considering the time sequence feature for assessing causality (see Box 2.6). For newly diagnosed cases, asking about past exposures usually guarantees that the exposure occurred before the disorder; but this cannot be assumed for participants with existing disease.
Researchers may also consider whether cases need to be free from other disorders (comorbidities).
Selecting the controls
A difficult design aspect is deciding who should be controls and how to select them [8], and this will also depend on resources and time available for the study. Box 6.5shows common sources of controls. It is important that controls are representative of the population of interest and that they have similar characteristics to the cases, with the exception of the exposure. If there really is no association between the exposure and outcome, the proportion of controls that is exposed should be the same as that for cases. Care must be taken to avoid choosing controls that lead to a bias, which over- or underestimates the association.
Approaching participants who could become controls may be straightforward if using a well-defined list (hospital/clinic list), or nominations directly from the case (family member or friend). However, using general population sources (e.g. register of residents or neighbour controls) requires careful planning. A random sample is needed because it would be impractical and unnecessary to include everyone. There are various methods of random sampling, ranging from simple random selection, to random sampling that targets groups of people with certain characteristics. Random digit dialling, which requires the person to have a telephone, also involves problems with trying to distinguish residential from business numbers, and people who do not pick up when they do not recognise the researchers’ telephone number (caller display on digital systems). Many numbers may need to be dialled, just to get one eligible study participant.
Box 6.1 illustrates the various ways in which controls could be selected (using the three examples covered in this chapter). The study of head circumference and Alzheimer’s disease used participants from another ongoing study, conducted at the same institution, from which the cases were identified. This is acceptable as long as the controls are considered to be appropriate comparators, that is, they have similar characteristics (which may not always be true if the other study has particular eligibility criteria).
Using hospital/clinic patients as controls is common. Access to these patients is easier than access to the general population, and several patient characteristics (e.g. age, gender, and ethnic origin) should already be available from the hospital database, and so can be used as selection or eligibility criteria. The key difference between these participants and those from the general population is that they all have a disorder, and it is therefore important to ensure that the disorder they have is not associated with the exposure of interest, because this is likely to dilute or mask the association between the disorder being investigated and the exposure.
For example, consider a case–control study to examine the relationship between smoking and lung cancer (Table 6.1). Cases would be patients diagnosed with lung cancer, but suppose the controls were people with heart disease. If people with heart disease had the same smoking prevalence as the general population, there would be no problem (80/20 = 4), but if a larger proportion of the heart disease controls smoked, this would underestimate the association between smoking and lung cancer (80/40 = 2).
Table 6.1 How selecting controls that have similar characteristics, and hence exposure (here smoking) status, to cases can underestimate the association, than if using general population controls.
| Cases with lung cancer | Hospital controls with heart disease | General population controls | |
| N = 100 | N = 400 | N = 1000 | |
| % of smokers | 80 | 40 | 20 |
| Risk ratio of smoking* | 1 | 2 | 4 |
* % cases ÷ % controls.
It is also possible to identify controls that overestimate an association. For example, if examining the relationship between the risk of colorectal cancer and using non-steroidal anti-inflammatory drugs (NSAIDs) [8], cases could come from a cancer clinic. If controls were selected from gastrointestinal clinics, they would presumably include a proportion with stomach ulcers, who would usually have been told to avoid NSAIDs. Because the proportion exposed to NSAIDs would be lower in this group than in the general population, the association between colorectal cancer and NSAIDs would be overestimated.
There may be situations where hospital controls could be a better match to cases than general population controls (see example in Box 6.4).
Should the controls be matched to cases?
The concept of attempting to ‘make everything the same’ between the exposed and unexposed group (see page 5), with the exception of the exposure status itself, was presented. Randomised clinical trials can achieve this at the design stage. For most observational studies, differences in potential confounding factors can only be allowed (adjusted) for at the end of the study, during the statistical analysis. However, in a case–control study, the situation can be somewhat different. Cases and controls are selected on the basis of their disease status, and the purpose is to compare the exposure status between them. Therefore, it is expected that the cases (with a disorder) and controls (without) would have different characteristics. Instead of trying to make the exposed and unexposed groups ‘the same’, researchers can attempt to achieve this with the cases and controls (matching). Interest is only in a specified exposure factor, which should be different between cases and controls if it has a real association with the outcome measure (i.e. the disease status).
A matched case–control study attempts to ‘make everything the same’ at the design stage. Researchers specify a few key factors, which are already known or expected to be important confounders. They then select one or more control participants who have the same features for the factors as one of the cases (called individual matching). This is the method used by the studies of SIDS and of cancer patients (Box 6.1). In the SIDS study, each control was carefully matched to be as close as possible to each case, using birth date (age) and geographical location. Therefore, the control group should be ‘the same’ as the cases, in terms of age and location, and any difference in the exposure status cannot be due to these two factors. There are several approaches to matching (Box 6.6). Matched controls can only be achieved if the matching factors are available from the sampling frame (or other source). If matching factors are not available, it might be possible to match by using initial information obtained from responders.
The simplest approach is not to match at all, which is commonly done. If there were no matching, an extreme observation could be that all the SIDS cases were aged <6 months old, and all the controls >12 months. It would then be impossible to separate out the effect of age from the disease status. The study of head circumference (Box 6.3) had no matching at all. In some cases the sampling frame for the controls is known to be generally similar to that for cases, so not having direct matching might be acceptable.
It is important in planning a study to specify how close the matching should be. For example, using exact age is ideal, but it might be difficult to get several controls with the same age as a case. The degree of matching could be relaxed, for example, using age within ±6 or 12 months, which is easier to do, although the greater the allowance, the more different the controls could become.
Determining the number of matching factors depends on the size of the sampling frame for controls. If there are many factors (e.g. ≥10) it will be difficult to find enough matched controls to choose from the sampling frame, unless the list contains a large number of individuals. This was the case for the study in Box 6.4(and Box 6.1), which attempted to match for six factors. The authors encountered great difficulty in finding suitable matched controls. Using between one and four matching factors would generally be reasonable. The researchers should agree the most important ones. There is a potential for overmatching, where the controls selected are so similar to cases that the exposure factor is also similar, and so the association either no longer exists or is diluted. This can arise when one or more of the matching (confounding) factors lies on the same biological/causal pathway as the exposure of interest.
An alternative to individual matching is frequency matching. Instead of finding controls for each case, based on one or more factors, a group of controls is found that is generally similar to the group of cases. For example, suppose two matching factors are age and smoking status. If, among 120 cases, 20% are aged 50–59 and they smoke, a similar proportion is randomly selected from controls with the same characteristics.
The physical act of selecting matched controls can be quite awkward to deal with, and so often requires the help of an IT programmer to write coding to do this electronically. Some researchers have the two lists (cases and controls) in front of them on paper, and manually select the controls, but this can be laborious and prone to error (especially with several matching factors). The process should ensure that a control is not selected for two or more cases, when using individual matching.
6.3 Measuring variables, exposures, and outcomes
In a case–control study, because the disease status of the cases and controls are known from the outset, the following are key considerations when measuring exposures and other factors (the same principles covered in Section 5.3):
- Standard, established, or generally accepted criteria should be used for diagnosing the cases.
- The exposures should always be assessed using the same methods for both cases and controls, to avoid bias.
- Where applicable (and possible), exposures should be assessed by researchers who do not know the case/control status of the participant (i.e. they are blind to this). If this is not possible, the main study hypotheses should be kept from those collecting data, particularly if they are to conduct direct interviews with the participants. This may be less of an issue if the data have already been recorded in, for example, hospital/medical records, when measures were taken before the current project was planned.
- Consideration could be given to whether controls should have baseline assessments to confirm that they do not have the disorder of interest (though sometimes this is not possible or feasible).
6.4 Collecting the data
As with other observational studies, data from case–control studies can be collected using a variety of sources (see Box 1.9)
Some case–control studies also involve collecting data from a proxy or surrogate, who could be a relative, next of kin, or possibly a friend. This is done when the case is unavailable, for example, has died or is unfit or unable to be interviewed or complete questionnaires.
As with cross-sectional studies, researchers on case–control studies should specify clearly, at the start, which information they require, because there is usually only one attempt to obtain this from the study participants or their proxy.
6.5 Sample size
All sample size estimations are guesses. There is nothing precise or accurate about them. Even with what appears to be reliable information used in the estimation, the achieved study size could still be too big or too small.
The number of ‘events’ (disorder, death, or other defined occurrence) matters greatly, in that it influences the reliability of the statistical analyses (see Box 3.8). A major advantage of a case–control study is that the researchers can choose the number of events (cases). Another key consideration is the number of controls. Some researchers believe that the more controls they include, the better, but while having up to four controls per case is appropriate, more than four does not significantly improve the reliability of the statistical analyses.
In the SIDS study in Boxes 6.1 and 6.2, four controls per case were chosen. With 196 cases, a target of 780 controls (4 × 196) was specified and achieved. In some studies, selected controls may be found subsequently to have missing key information, and so may be excluded from the statistical analysis. Therefore, although researchers specify the target number of controls per case, the number actually recruited and analysed may be less. The study on Alzheimer’s disease did not specify a target number of controls, because the size of this group was already fixed (they came from an ongoing study). In this situation, there were more cases than controls (592 vs. 459), which is generally not a problem, as long as the control group is sufficiently large.
Information needed for sample size estimation when examining associations
When case–control studies aim to examine the effect of a single exposure factor on a single outcome measure (e.g. disorder), several pieces of information are needed for the sample size calculation (Figure 6.2). Items such as the percentage of controls expected to be classified as exposed should ideally come from prior information.
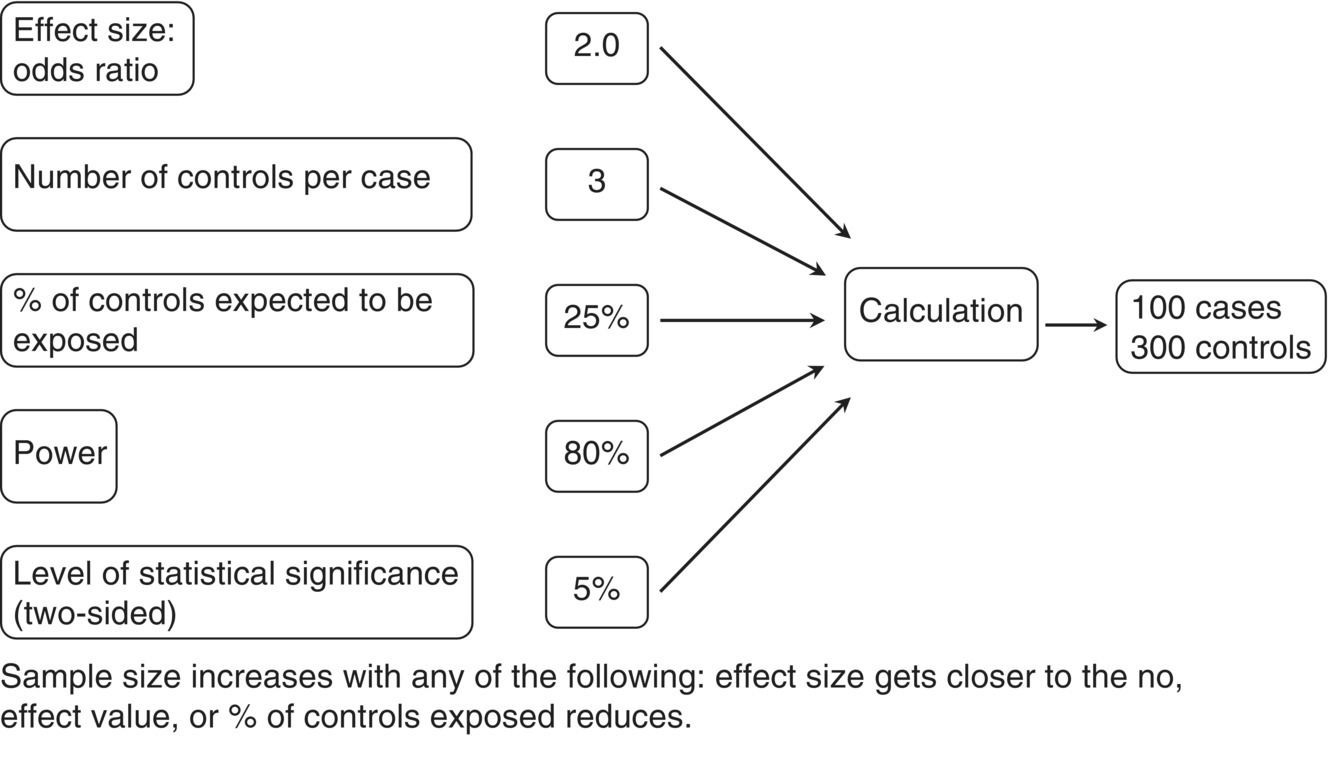
Figure 6.2 Information required for a sample size estimation for case–control studies in which the effect size is an OR.
The magnitude of the effect size (odds ratio OR) could be based on previous knowledge or one that is judged to be associated with a minimum clinically important effect. The smaller the expected effect size, the larger the study that is required. In the example in Figure 6.2, the OR is 2.0 (a reasonably large effect), and this requires 400 participants (100 cases and 300 controls). If the OR were 1.5, the study size would greatly increase, to 1200 participants (300 cases and 900 controls). Choosing a sample size that seems feasible in a certain time frame and then specifying the effect size is an inappropriate approach, because the effect size could be quite different in reality from what was expected. The sample size estimate only reflects the contributing assumptions. If the assumptions are unrealistic, the size of the study will be too small or too large.
There are several methods available to calculate the sample size from statistical packages and software [9, 10], including those freely available for observational studies [11].
When the outcome measure is based on ‘counting people’ or time-to-event data (both use risk), the number of events is often more important than the total number of participants in the study. For ‘taking measurements on people’, the standard deviation of the endpoint will influence study size (little variability between participants requires a smaller study).
In Figure 6.2, the level of statistical significance is the chance of finding an effect when in reality one does not exist, so the conclusion of the study would be wrong. It is essentially an error rate, and is often set at 5% (0.05). The results will be determined to be statistically significant at this level, which is generally regarded to be sufficiently low before making conclusions about the association. A lower error rate (1%) may be used, which increases sample size.
Power can be interpreted as the chance of finding an effect size of the magnitude specified, if it really exists. Most studies use a high power, such as 80 or 90%. Using the example in Figure 6.2, if the true OR is at least 2.0, a study size of 400 participants should mean that there is an 80% chance of finding this size of effect or greater and that it would be statistically significant at the 5% level. Increasing power will increase the sample size.
The method of sample size calculation depends on the type of outcome measure and effect size used:
- Counting people (OR)
- Taking measurements on people (mean difference)
- Time-to-event data (hazard ratio)
When there are several exposures to examine, and no one particular exposure has been designated as the item of interest, estimating sample size is complex. An estimate could be made for each factor, and a simple approach would be to then take the largest sample size. However, if this size is unfeasible, it may be appropriate to attempt to reduce the number of exposures, and to identify two or three key factors, for which sample sizes could then be examined. If the researchers plan to include all the factors in a multivariable regression analysis, at least 10 events (cases) would be required [12]; this would not involve the concept of statistical power.
6.6 Analysing data and interpreting results
Prevalence and incidence are useful ways of measuring disease occurrence (see Box 2.2). Prevalence can be estimated from cross-sectional studies, and incidence from cohort studies; however, case–control studies include a specified number of cases and controls (determined by the researchers), so it is not possible to obtain either prevalence or incidence.
Continuous exposure variables can be divided into groups of similar size, such as tertiles or quartiles (see page 76). However, rather than combining cases and controls, just using the controls (i.e. those without the disorder of interest) should give a clearer association between the exposure and outcome. If there is a relationship, the cases (those with the disorder) should tend to have values at one end of the distribution. Using all the study participants to define the cut-off points will yield an artificial ratio of cases to controls (i.e. chosen by the researchers), and because this does not reflect the actual incidence, the cut-off points could dilute or mask an association. Also, if using only controls to define the cut-off points, the group should be more homogenous.
A table showing the key (baseline) characteristics in cases and controls separately, is useful to see how comparable they are.
6.7 Outcome measures based on ‘counting people’ endpoints: Sudden infant death syndrome and sleeping factors (Box 6.2)
Measuring variables, exposures, and outcomes
The participants in this study were the mother–baby pair. The outcome measure related to the health of the baby, while the data on exposures were reported by the mother, and based on her characteristics, the home environment, and the baby’s sleeping environment.
There were many exposures (risk factors) in this study, with a focus on how babies were put to bed, particularly sleeping position. The cases (specifically mothers) had to remember several details about the last night the baby was alive, as well as much information about the living environment and her own characteristics. The questionnaire had over 600 items, completed by the mother while the researcher was present. Even a factor like ‘sleeping position’ (back, side, or face down), which initially appears straightforward, requires thought: there is the position in which the mother put the baby to bed, and the position in which the baby was found after death.
A common potential problem in case–control studies is recall bias (see Box 1.6). Because the case has suffered a health-related event, they might be more likely to recall past information more accurately, or possibly over-report exposure status, than controls, who have not had any such event triggered. However, it is also possible in this situation that some mothers might not be able to report information with sufficient accuracy, due to the stressful nature of the topic (the baby would only have died a few days before the interview).
The outcome measure was the occurrence of SIDS, which was diagnosed through routine clinical practice. The control group was babies who were alive.
Analysing data and interpreting results
In a study such as this, in which many variables (>600) were measured performing numerous analyses may lead to a loss of focus on the main exposures of interest. Sleeping position (i.e. whether the baby was put to bed on the front, back, or side) had already been known to be associated with SIDS. This study aimed to confirm the finding, and to also find other potential risk factors. When planning this study, the researchers did not have a specific exposure in mind. Here, it is essential that multivariable statistical analyses are used (see page 77). An exposure of interest in one analysis would be a potential confounding factor in another, and the simultaneous effect of all the factors on the risk of SIDS needs to be examined.
The outcome measure (chance of having a baby with SIDS) was analysed using a logistic regression (see page 69). Matching was used to select controls, and this was taken into account in the analyses using conditional logistic regression for matched case–control studies. Essentially, the data were analysed within each matched set, which is not the same as adding the matching variables as cofactors to the regression model.
What are the main results?
Table 6.2is typical for a case–control study. Sometimes, the reference group, which we call unexposed, is obvious, for example, never-smoker in a study of cancer and cigarette smoking. In the SIDS study, the reference group was chosen as the ‘back’ sleeping position, probably because this was already recommended as public health policy at the time.
Table 6.2 Summary table showing all three exposure groups and the odds ratios (ORs) taking into account the matching factors between the cases and controls.
| Sleeping position (when put to bed) | Case (baby died from SIDS) | Control (baby alive) | ORs | |
| Allowing for the matching factors? | ||||
| No* | Yes** | |||
| Back# | 82 | 509 | 1.0 | 1.0 |
| Side | 76 | 241 | 1.96 | 2.01 |
| Front (face down) | 30 | 24 | 7.76 | 9.58 |
*Can be calculated by hand (e.g. for front vs. back) as follows:
Odds of SIDS in the exposed group: 30/24 = 1.25.
Odds of SIDS in the unexposed group: 82/509 = 0.161.
OR = 1.25/0.161 = 7.76.
**Calculated using a conditional logistic regression.
#Chosen to be the reference group.
The aim is to compare the risk of SIDS between the exposed and unexposed groups, to produce a relative risk (see Chapter 3, page 48). However, risk cannot be calculated in a case–control study because the number of cases and controls is artificial, so we cannot obtain either a correct numerator or denominator for risk. Instead, the odds of having a baby with SIDS is obtained (Table 6.2) in each exposure group, from which the OR can be calculated. Because SIDS is quite uncommon (about 1 in 500 births in the UK in the 1980s), the OR should be a good estimate of the relative risk (see Table 3.2). In the example, it is 7.76, meaning that if the baby were put to bed on its front, it was almost eight times more likely to die from SIDS than a baby on its back. This is a very large effect.
This is a crude OR (ignoring matching), but it is common practice to report the estimate after allowing for the matching factors (here, age and geographical location) using a conditional logistic regression (Table 6.2). Babies put to bed on their sides had twice the risk of SIDS compared with those put down on their backs, and the risk was more than 9 times higher for those on their front. The results in Table 6.2focus on the sleeping position of the baby and confirm the findings and conclusions from previous studies.
Table 6.3shows the association between SIDS and several factors of interest. Although the first column is labelled ‘univariable (unadjusted)’, the ORs have already allowed for the matching factors (age and geographical location). The reason for this labelling is that the matching factors have not been treated in the same way as the other variables in the regression model.
Table 6.3 Factors associated with the sleeping environment.
| Univariable odds ratio (unadjusted) | Multivariable (adjusted) odds ratio | |
| Sleeping position: | ||
| Front (prone) | 9.58 (4.86–18.87) | 9 (2.84–28.47) |
| Side sleeping | 2.01 (1.38–2.93) | 1.84 (1.02–3.31) |
| Found with covers over head | 18.93 (8.05–44.48) | 21.58 (6.21–74.99) |
| Bedding: | ||
| 6–9 togs** | 1.5 (0.99–2.26) | 0.89 (0.45–1.76) |
| ≥10 togs** | 3.38 (1.94–5.87) | 0.94 (0.31–2.83) |
| Wearing hat | p = 0.015* | 4.13 (0.22–77.89) |
| Heating on all night | 2.14 (1.30–3.50) | 2.37 (0.96–5.84) |
| Mothers who ever breastfed | 0.5 (0.35–0.71) | 1.06 (0.57–1.98) |
| Shared bed with parents | 4.12 (2.30–7.40) | 4.36 (1.59–11.95) |
| Used dummy (pacifier) | 0.59 (0.42–0.84) | 0.38 (0.21–0.70) |
| Used duvet | 2.82 (1.95–4.08) | 1.72 (0.90–3.30) |
| Loose bed covering | 1.92 (1.35–2.73) | 1.07 (0.61–1.89) |
Adjusted for maternal age, parity, gestation, birthweight, whether family received income supplement, exposure to tobacco smoke, and the sleeping factors in the table that remained statistically significant after adjustment.
*OR not reliable because of small numbers (p-value from Fisher’s exact test).
**‘Tog’ is a measure of the warmth (thickness) of the bedding/duvet.
The reference (comparison) group for each factor is not shown in the table, to avoid having multiple rows with OR 1.0. It is the opposite of what is shown for all factors, for example, the reference for ‘mothers who ever breastfed,’ is ‘mothers who never breastfed,’ except for sleeping position (reference is ‘back’ and for bedding ‘<6 togs’).
Table 6.3is useful because it shows the association between each exposure factor individually and also when adjusted for other factors. Because there is interest in whether the size of the effect changes, and whether it moves closer to the no effect value, both unadjusted and adjusted effect sizes should be reported (Figure 6.3).
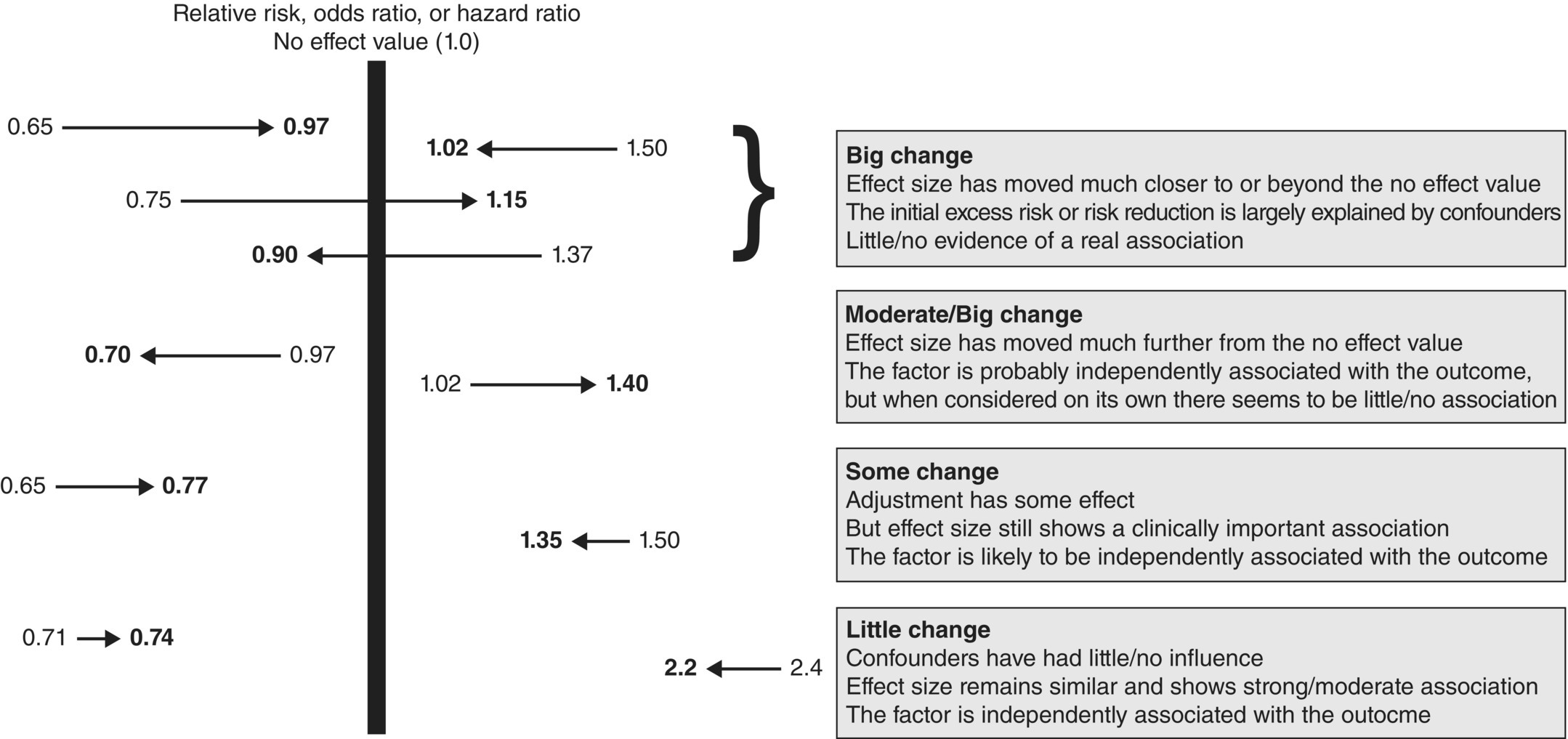
Figure 6.3 How effect sizes for a factor could change after adjustment for confounders. The arrow shows the direction, moving from unadjusted (crude) estimate to adjusted (shown as bold). The 95% CIs also need to be interpreted, in terms of whether they include the no effect value or not.
Box 6.7is an interpretation of the results in Table 6.3. ORs above 1.0 indicate that the risk of SIDS increased compared with the reference group, and those below 1.0 indicate a protective effect (risk decreased). The more extreme the value, the stronger the risk factor (Figure 3.1). Those with the strongest association are, in order of magnitude, as follows: ‘found with covers over head’ (OR 21.58), ‘sleeping on front’ (OR 9), ‘sharing bed with parents’ (OR 4.36), and ‘using dummy/pacifier’ (OR 0.38). Because these effects remained similar and statistically significant after adjustment, they could be referred to as independent risk factors, and this is one of the features for causality (Box 2.6).

Full access? Get Clinical Tree


