OUTLINE
Uses of Buffers and pH Adjusting Agents
Selecting a Buffer System or a Compound to Adjust pH
Acidifying, Alkalizing, and Buffering Agents
I. DEFINITIONS
A. An acid may be defined as
1. A substance that, when dissolved in water, yields hydrogen ions, H+ (Arrhenius theory).
2. A species that yields protons, H+ (Bronsted-Lowry theory).
3. An electron pair acceptor (Lewis theory).
B. A base may be defined as
1. A substance that, when dissolved in water, gives hydroxide ions, OH− (Arrhenius theory).
2. A species that can accept a proton (Bronsted-Lowry theory).
3. An electron pair donor (Lewis theory).
In pharmaceutical systems, we usually are dealing with solutions that contain water; therefore, the Arrhenius and Bronsted-Lowry definitions are most suitable for our purposes.
C. A buffer is a compound or a mixture of compounds that, when present in a solution, resists changes in the pH of the solution when small quantities of acid or base are added to the solution.
D. Buffer capacity is a measure of the resistance to change in the pH of a solution when acids or bases are added to the solution.
E. Many useful equations have been derived to deal with the subject of acid-base chemistry. A list of those equations most useful in pharmaceutical systems is given in Table 18.1. Example calculations using these equations are also given.
II. USES OF BUFFERS AND pH ADJUSTING AGENTS
Buffers or agents to adjust the pH of solutions may be added to manufactured pharmaceutical products or to extemporaneously compounded preparations for any of the following reasons:
A. For preparations that are intended to be applied to the sensitive membranes of the eye or nasal passages or that may be injected into muscles, blood vessels, organs, tissue, or lesions, it is desirable to adjust the pH of the preparation to a level that is close to the physiologic pH of the tissue. This is done to minimize tissue damage and pain or discomfort experienced by the patient.
B. The absorption, and therefore the therapeutic effectiveness, of certain drugs may be improved when they are present either in an ionized or nonionized state. This state may be manipulated and maintained by adjusting the pH of the medium.
C. The chemical stability of many drugs in solution may be improved by maintaining the pH of the solution in a particular range.
D. The aqueous solubility of many organic drugs depends on the degree to which these weak electrolytes are present in ionic form. This, in turn, may depend on the pH of the solution.
III. BUFFER CAPACITY
A. Buffer capacity, β, is defined by the formula:
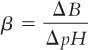
where ΔB is the gram equivalents per liter of strong acid or strong base added to the buffer solution and ΔpH is the resulting pH change. The larger β is, the greater the buffer capacity of the system (that is, its ability to resist a pH change).
B. While buffer capacity can be determined for a system by using the formula just given, it is not often calculated in compounding situations. Because of the limited beyond-use datings needed for compounded drug preparations, exact buffer capacities are not required. For a detailed treatment of the subject of buffer capacity, refer to a book on physical pharmacy (1).
C. Even though we rarely calculate buffer capacity, it is helpful to understand the concept in principle and to understand the circumstances under which buffer capacity is maximized.
1. Solutions of strong acids such as HCl will resist a change in pH at or below pH 3. In fact, the standard buffer solution identified by the USP for the pH range 1.2 to 2.2 is a 0.2 M solution of HCl to which KCl has been added as a neutral salt for proper electrolyte concentration (2).
2. Similarly, strong bases such as NaOH give good buffer capacity at pH 11 or higher.
3. The most common buffer systems consist of a combination of a weak acid and its salt (i.e., its conjugate base) or a weak base and its salt (i.e., its conjugate acid).
a. The Henderson-Hasselbalch equation, also known as the buffer equation, relates the pH of a solution, which contains an acid-base conjugate pair, to the pair’s dissociation constant and the concentrations of the species in the solution. This equation and sample problems are shown in Table 18.1.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


