OUTLINE
Quantity Expressions and Calculations Used in Drug Therapy
Concentration Expressions and Calculations Used in Drug Therapy
Methods of Calculating Quantities and Concentrations When Combining or Diluting Preparations
Special Calculations Involving Alcohol USP
Special Calculations Involving Concentrated Acids
Special Calculations Involving Formaldehyde Solutions
Calculations Involving Salts and Compounds Containing Water of Hydration
I. INTRODUCTION
A. An essential function of pharmacy service is to ensure that patients get the intended drug in the correct amount. These are two important components of the five recognized “rights” of patients in receiving medication: the right drug in the right dose by the right route of administration to the right patient at the right time. Although providing the correct drug in the correct amount is considered a basic right of medical care, the difficulty of ensuring that it occurs for all patients 100% of the time is evident in the various studies of medical errors, including the famous 1999 Institute of Medicine report, “To Err Is Human.” The health professions continue to struggle with this issue; improper dose/quantity continues to be in the top tier of causes of medication errors as reported by hospitals that are part of USP’s MedMARx error reporting network (1). Although medication safety is a joint responsibility of all members of the health care team, it is clearly an area in which pharmacists and pharmacy technicians can and do play a major role.
B. Basic to providing correct doses of drugs to patients is a firm understanding of units of measurement for drugs, accepted expressions of quantity and concentration for drug products and preparations, and knowledge and skill in using this information to perform the calculations needed in providing correct and intended drug therapy. Systems and units of measurement and basic calculations techniques were presented in Chapter 7; this forms the basis for the current chapter on quantity and concentration expressions and calculations, which, in turn, will be used in Chapter 9 for calculating and evaluating appropriate doses and dosage regimens. This information will also be used in later chapters of this book when sample prescription and medication orders are evaluated. Most important, this composite information and skill set is vital to providing safe and effective therapy to patients.
C. In general, the following factors determine the accepted method for representing the quantity of a drug and the concentration of the drug in a dosage form.
1. Accurate representation of the quantity of active moiety, a drug molecule or ion, acting at a receptor
2. Convenience of measurement
3. Route of administration
4. Tradition
II. QUANTITY EXPRESSIONS AND CALCULATIONS USED IN DRUG THERAPY
A. Metric (SI) weights and volumes
1. Quantities for drugs and dosage form ingredients are most often expressed as either metric weights or volumes.
2. The metric (SI) system is described in Chapter 7, and the metric units of weight and volume most commonly used in pharmacy and medicine are given in Table 7.2 of that chapter.
3. Chapter 14 contains information on the use of balances and volumetric apparatus to measure weights and volumes of drugs, dosage forms, and compounding ingredients. The use of this equipment is demonstrated on the CD that accompanies this book, and multiple examples of the proper use of weighing and measuring equipment are given in the dosage forms chapters in this book.
B. Biological units of activity
1. Biological units of activity are used for certain natural products including insulin, heparin, and some antibiotics, vitamins, anticancer agents, biotechnology drugs, vaccines, and miscellaneous others.
2. The units are specific to each drug or natural product with the standards set in the United States by the FDA and USP and internationally by the World Health Organization.
3. In most cases, the standards give an accepted metric weight equivalent or range. For example, the USP monograph for Insulin Human USP states, “Its potency, calculated on the dried basis, is not less than 27.5 USP Insulin Human Units in each mg” (2). Sample Prescription 25.3 in Chapter 25 uses nystatin powder to illustrate the conversion between units of activity and metric weight in milligrams when compounding with a drug that has its dose expressed in biological units of activity.
4. Insulin is the most common drug with potency expressed in units. To facilitate the use and administration of insulin by patients, special syringes are available with volumes marked in units. Caution must be exercised when using these syringes because the markings are specific to a particular strength of insulin product. For example, the unit markings on a U-100 insulin syringe can be used to measure only insulin, and only U-100 insulin (that is, insulin that has a concentration of 100 units/mL).
C. Molecules, moles, and millimoles
1. The most fundamental unit of active ingredient acting on a biological receptor is a drug molecule or ion. However, a molecule of a substance is too small a quantity to be pharmaceutically useful because we always deal with fairly large numbers of molecules. It is therefore convenient to measure in terms of a larger unit. Usually the unit used for this purpose is the mole (SI symbol, mol), which is Avogadro’s number (6.023 × 1023) of molecules.
2. Because we cannot count out molecules or directly measure moles, a method is needed to equate these units with a quantity that we can measure. The molecular weight (MW) of a compound is the weight in grams of 1 mole of the compound; that is, it is the weight in grams of 6.023 × 1023 molecules. For example, the MW of water is 18.0, meaning that 18.0 g of water contains 6.023 × 1023 molecules of water. Similarly, the MW of phenobarbital is 232.2, meaning that 232.2 g of phenobarbital contains 6.023 × 1023 molecules of phenobarbital. Because elements, ions, and molecules react in integral ratios (1:1, 1:2, and so on), the mole is a more fundamentally useful unit than is the gram, but the gram offers convenience of measurement.
3. Millimole (mmol) units are often used in pharmacy and medicine rather than moles because the required quantities and concentrations of drugs are relatively small. There are 1,000 mmol/mol of a compound. The number of grams per mole (g/mol, the molecular weight) is also equal to the number of milligrams per millimole (mg/mmol); for example, 1 mmol of phenobarbital weighs 232.2 mg.
4. One example of a drug that traditionally has its dose expressed in millimoles is phosphate when administered in total parenteral nutrition (see Chapter 35). In this case, we are interested in the amount of phosphorus, the P part of the phosphate, and we need a way to get at this. One millimole of phosphate, whether in the form H2PO4−1, HPO4−2, or PO4−3, contains the same amount of phosphorus, P, but all three forms have different weights (and different numbers of milliequivalents).
Examples 8.1 and 8.2 demonstrate conversions between metric and molar units.
Calculate the weight in grams from moles:
You have a formula that calls for 0.5 moles of Sodium Hydroxide (NaOH). Sodium Hydroxide is available as a solid. How many grams of NaOH should you weigh? The MW of NaOH = 40.0.
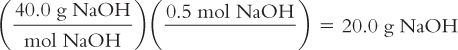
Calculate millimoles from weight in milligrams:
You have a liquid formulation that contains 600 mg of Potassium Chloride (KCl) in each teaspoonful of syrup. You want to know how many millimoles of KCl are in each teaspoonful. The MW of KCl = 74.5.
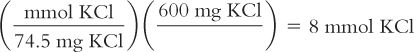
D. Equivalents and milliequivalents
1. When dealing with electrolytes in solution, we are at times interested in only one of the ion pair. For example, with mineral acids, we may be interested only in the number of H+ ions in solution. We do not care about the counter ion, the Cl−, the 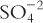 , the
, the  , and so on. Therefore, we do not care about the weight of the acid present or the number of moles of compound present; we want to know how many moles of H+ are present. The concept of equivalents evolved from this special need.
, and so on. Therefore, we do not care about the weight of the acid present or the number of moles of compound present; we want to know how many moles of H+ are present. The concept of equivalents evolved from this special need.
2. Equivalents (Eq), sometimes referred to as combining power, are the number of univalent counter ions needed to react with each molecule of the substance. Hydrochloric acid (HCl) has 1 Eq/mol because 1 mole of the univalent ion OH− reacts exactly with one mole of H+ in HCl. (Also note that one mole of Na+ reacts exactly with one mole of Cl− in HCl.) Sulfuric acid (H2SO4) contains 2 Eq/mol because 2 moles of OH− are required to react with 1 mole of sulfuric acid. The compound Al2(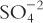 )3 has 6 Eq/mol because, in aqueous solution, two Al+3 ions are obtained for each Al2(SO4)3, and they would react with six univalent anions, such as six Cl−s. The sulfate (3
)3 has 6 Eq/mol because, in aqueous solution, two Al+3 ions are obtained for each Al2(SO4)3, and they would react with six univalent anions, such as six Cl−s. The sulfate (3 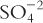 ) also reacts with six univalent counter ions, such as six Na+s.
) also reacts with six univalent counter ions, such as six Na+s.
3. The definition of equivalent depends on the particular type of reaction undergone, so it is subject to some ambiguity. The number of equivalents per mole for electrolytes with variable valence, such as phosphate and carbonate, depends on the pH of solution: For instance, Na2HPO4 with 2 Eq/mol is predominant at high pH, whereas NaH2PO4 with 1 Eq/mol predominates at lower pH. For this reason, phosphate concentration for replacement therapy is expressed in terms of millimoles rather than as milliequivalents.
4. As with moles, equivalents cannot be measured directly, so a method is needed to equate these units with a quantity that we can measure. The equivalent weight or gram-equivalent weight (Eq) of an element or compound is that weight in grams which combines chemically with one equivalent of another element or compound. The equivalent weight of HCl is its molecular weight, because this compound has 1 equivalent per mole and reacts with one equivalent of another compound. The equivalent weight of sulfuric acid is its molecular weight divided by two because sulfuric acid has 2 equivalents per mole. The equivalent weight of aluminum sulfate is its molecular weight divided by six because there are 6 equivalents per mole. This can be expressed by the general equation:
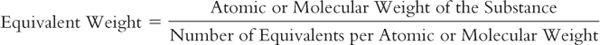
5. Milliequivalents (mEq), rather than equivalents, are often used in pharmacy and medicine because, when dosing electrolytes, we are usually dealing with small quantities. There are 1,000 mEq per equivalent. The number of equivalents per mole for a given compound equals the number of milliequivalents per millimole for that substance.
6. Electrolytes such as potassium, sodium, calcium, and chloride often are dosed in terms of milliequivalents because, from a therapeutic point of view, it is the individual ion that is of interest. Often the method of expressing the dose of an electrolyte may be a matter of tradition. For example, oral doses of calcium usually are given in terms of milligrams or grams of the compound (e.g., calcium carbonate 500 mg), whereas parenteral electrolyte replacement doses of calcium are more often expressed in terms of milliequivalents (e.g., Ca++ 4.6 mEq).
7. There is a trend toward expressing electrolyte doses in terms of milligrams or millimoles of the pertinent ion rather than as milliequivalents of the ion or grams or milligrams of the salt. This method has the advantage of being unambiguous, and it is the system now used internationally; equivalent (Eq) is not a recognized SI unit. As is often the case when there is a change in systems, errors of misinterpretation can occur; there have been reports of doses written in terms of milligrams of the salt (e.g., 500 mg Calcium Chloride) and interpreted and administered as milligrams of the ion (e.g., 500 mg calcium ion, which is 1,836 mg of the Calcium Chloride, nearly a fourfold overdose). Pharmacists must be very careful when interpreting these orders. Fortunately, product labeling and therapeutic reference books now usually give concentrations in all three systems [e.g., Calcium Chloride 10% Injection (1 g/10 mL; each milliliter of solution provides 27.2 mg or 1.36 mEq of calcium)].
Examples 8.3 through 8.5 show calculations for converting between milliequivalents and milligrams of ions and metric weights of salts.
Calculate weight in milligrams of the salt from milliequivalents:
A potassium supplement tablet contains 10 mEq of KCl. How many milligrams of KCl are in each tablet? The MW of KCl = 74.5
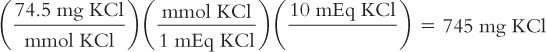
Calculate weight in milligrams of salt from milligrams of the ion.
A dose of calcium chloride is prescribed as 136 mg of calcium ion. How many milligrams of calcium chloride are needed for this dose? Calcium chloride is available as the dihydrate (CaCl2· 2H2O), which has a MW = 147; calcium ion has an atomic weight of 40.
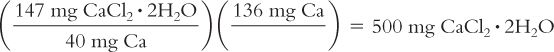
Calculate milliequivalents from weight in milligrams of salt:
The powder for oral solution for a bowel-cleansing product contains 568 mg of anhydrous sodium sulfate (Na2SO4). How many milliequivalents of Na+ are in this product? The MW of Na2SO4 = 142.
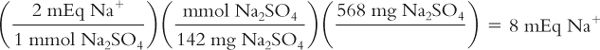
(For an alternative way of conceptualizing and solving this problem, see the CD that accompanies this book.)
1. Osmotic pressure is discussed in Chapter 11, Isotonicity Calculations. Basically, pharmaceutical solutions that come in contact with cell membranes should have the same osmotic pressure as the cell contents to prevent tissue damage and discomfort. Because osmotic pressure is a colligative property, it depends on the number of individual solute particles (ions or molecules) per given volume of solution.
2. An osmole (Osmol) is the number of moles of solute present multiplied by the number of particles per molecule obtained when the solute is dissolved in water. Nonelectrolytes, such as dextrose, do not dissociate in solution, so 1 mole of dextrose yields 1 osmole. Sodium chloride dissociates into two ions in aqueous solution, so 1 mole of sodium chloride gives 2 osmoles. Sodium sulfate (Na2SO4) gives three ions per molecule, so there are 3 osmoles per mole of sodium sulfate.
3. Milliosmole (mOsmol) units, rather than osmoles, are often used in pharmacy and medicine. There are 1,000 mOsmol per Osmol. The number of osmoles per mole for a given compound equals the number of milliosmoles per millimole for that substance.
4. If a drug or chemical is present in solid form as a hydrate (e.g., MgSO4·H2O), the water molecules do not count as particles because they merely become part of the solvent in aqueous solution.
Examples 8.6 and 8.7 show calculations for converting between osmole and metric units.
Calculate osmoles from weight in grams:
Isotonic Sodium Chloride Solution (0.9%) has 9 grams of NaCl in each liter of solution. How many osmoles are there in each liter of solution? The MW of NaCl = 58.5.
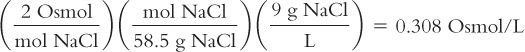
Calculate milligrams from milliosmoles:
You want to add solute to a liter of water so that there are 300 mOsmol in this solution. Your source of solute is Magnesium Sulfate Heptahydrate (MgSO4·7H2O), which has a MW = 246.5. How many milligrams of this solute should you add?
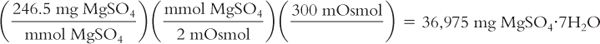
III. CONCENTRATION EXPRESSIONS AND CALCULATIONS USED IN DRUG THERAPY
A. Concentration gives quantity of drug or active ingredient per amount (volume or weight) of product or preparation.
1. Concentrations are used for expressing doses for all topical preparations. In this case, concentration has conceptual importance because concentration gradient is the driving force for transfer of the drug across the membrane or barrier, such as the skin.
2. Concentration also is used to express the strength of liquid systemic products—for example, amoxicillin suspension 250 mg/5 mL, or dextrose 5% injection.
3. For individual dosage units such as capsules, tablets, and suppositories, the dose is expressed as a quantity of drug rather than as a concentration. However, because pure drug is almost never dispensed, these quantities are really concentrations. For example, when the label on a bottle of acetaminophen states “Acetaminophen 500 mg,” what this really means is acetaminophen 500 mg per tablet. Because the tablet usually contains other ingredients (e.g., pharmaceutical ingredients such as binders, disintegrants, lubricants) in addition to the acetaminophen, the tablet weighs more than 500 mg; the content could be expressed as a concentration, such as acetaminophen 500 mg per 750 mg of tablet material.
B. Metric units of weight and volume
Metric units for weight and volume can be combined to give expressions of concentration.
1. Weight of active ingredient per weight of product: For example, gentamicin ophthalmic ointment 3 mg per gram (also written 3 mg/g) is 3 mg of gentamicin in each 1 g of ointment.
2. Weight of active ingredient per volume of product: For example, tobramycin ophthalmic solution 3 mg per milliliter (also written 3 mg/mL) is 3 mg of tobramycin in each 1 mL of solution; amoxicillin suspension 250 mg per 5 mL (also written 250 mg/5 mL) is 250 mg of amoxicillin per 5 mL of suspension.
C. Molarity and molality
1. Molarity (M) is the number of moles of solute per liter of solution. For example, a 1 M solution of sodium hydroxide contains 1 mole of sodium hydroxide per liter of solution. Because the molecular weight of sodium hydroxide is 40.0, a 1 M solution of sodium hydroxide contains 40.0 grams of sodium hydroxide per liter of solution (40 g/L) or 40 mg/mL.
2. Molality (m) is the number of moles of solute per 1,000 grams of solvent.
3. For dilute aqueous solutions, the numeric values of molarity and molality are nearly equal. This is because water has a density of 1.0 g/mL, so one liter weighs 1,000 grams. Furthermore, for dilute solutions the quantity of solute is small and therefore takes up very little volume in the solution, and the density of the solution is also very close to 1.0 g/mL. This does not hold true for more concentrated solutions in which there is a large amount of solute and when the densities of the solvent and solution are not equal to 1.0. The example given below for Syrup NF is a good illustration of the large difference in molarity and molality for a concentrated solution.
4. Other molar concentration terms used in pharmacy include millimoles per milliliter (mmol/mL) or millimoles per liter (mmol/L).
Examples 8.8 through 8.11 show methods of converting between molar and molal concentrations and metric quantities and concentrations.
Calculate molarity from grams of solute per 100 milliliters of solution:
Diluted Hydrochloric Acid NF contains 10 g of HCl in 100 mL of solution. Calculate its molarity. The MW of HCl = 36.5.
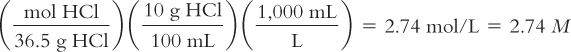
Calculate the grams of solute needed for a desired volume of M solution:
You want to make 500 mL of a 3 M solution of NaOH. How many grams of NaOH do you need? The MW of NaOH = 40.0.
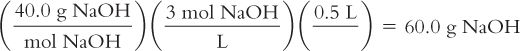
Calculate the molarity and the molality of a solution from its weight/volume concentration and the density of the solution.
Syrup NF contains 850 g of sucrose in 1,000 mL of solution. The solution has a density of 1.3. The MW of sucrose = 342.
Molarity (M) of the solution:
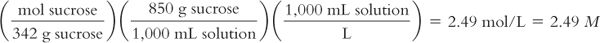
Molality (m) of the solution:
Because molality is based on kilograms of solvent, to calculate the molality of the solution, we first must calculate the weight of the solution using its density and then use this information to calculate the weight in kilograms of the solvent, water.
Weight of 1 L of solution:
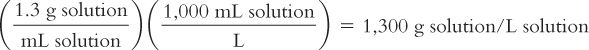
Remembering that weights are additive:
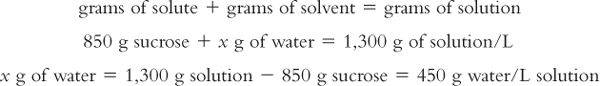
Calculation of molality of the solution:
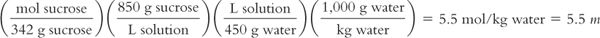
For those of you who like using formulas, molarity and molality can be interconverted using the formula:
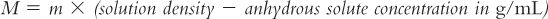
In this example, to convert from M to m, solve for m:
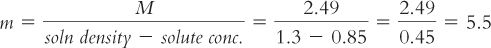
Calculate millimoles per liter (mmol/L) from milligrams per deciliter (mg/dL or mg%):
To conform to the international system of units, reporting of cholesterol blood plasma levels has changed from milligrams per deciliter (1 dL = 100 mL), sometimes referred to as mg%, to millimoles per liter. A patient’s medical record from a former hospitalization shows a cholesterol level of 230 mg/dL. What is the equivalent of this level in mmol/L? The MW of cholesterol = 387.
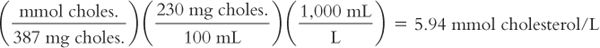
D. Normality and milliequivalents per milliliter (mEq/mL)
1. Normality (N) is the number of equivalents per liter of solution. A 1 N solution of HCl has 1 Eq/L. Because the MW of HCl is 36.5 g and because there is 1 Eq/mol, a 1 N solution has 36.5 g of HCl per liter of solution, and a 1 N solution of HCl equals a 1 M solution of HCl. A 1 N solution of sulfuric acid also has 1 Eq/L. However, because sulfuric acid has 2 Eq/mol, a 1 N solution of sulfuric acid has 49.0 g (half the molecular weight) of sulfuric acid per liter of solution. In this case, a 1 N solution of H2SO4 equals a 0.5 M solution of H2SO4. Both solutions, 1 N HCl and 1 N H2SO4, provide the same number of H+ ions in each liter of solution.
2. Other concentration terms used in pharmacy include milliequivalents per liter (mEq/L) and milliequivalents per milliliter (mEq/mL).
Examples 8.12 and 8.13 show methods of converting between concentrations in metric units and normality and mEq/mL concentrations.
Calculate grams per liter from normality:
You want to make 500 mL of a 1 N solution of sulfuric acid (H2SO4). How many grams of H2SO4do you need? The MW of H2SO4 = 98.1.
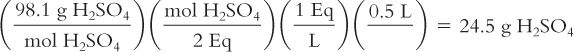
Calculate milliequivalents per milliliter from grams per milliliter:
You have a pint of potassium chloride syrup that is labeled 10% (10 g KCl per 100 mL of syrup). The dose of this liquid is 1 tablespoonful (i.e., 15 mL). You want to know the number of milliequivalents of K+ in each dose. The MW of KCl = 74.5.
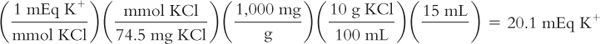
E. Osmolality and osmolarity
1. The concepts of osmolality and osmolarity apply to aqueous solutions in contact with biological membranes. Expressing concentrations of pharmaceutical solutions in osmolar terms is important when evaluating the appropriateness of solutions that come in contact with sensitive body membranes and tissues.
2. Osmolality is the number of osmoles per kilogram of the solvent water. For an aqueous solution of a nonelectrolyte that behaves ideally (no dissociation or association), a 1 m solution has an osmolality of 1 Osmol/kg of water. For an aqueous solution of a univalent-univalent electrolyte such as NaCl, if behaving ideally and giving two ions per molecule, a 1 m solution would have an osmolality of 2 Osmol/kg of water.
3. Osmolarity is the number of osmoles per liter of solution. For a compound that does not ionize in water, a 1 M solution has an osmolarity of 1 Osmol/L of solution. For an aqueous solution of the univalent-univalent electrolyte NaCl, if behaving ideally and giving two ions per molecule, a 1 M solution would have an osmolarity of 2 Osmol/L of solution.
4. As with molarity and molality, the numeric values for osmolality and osmolarity are very close in dilute solutions but can vary substantially with concentrated solutions. This is clearly illustrated with the 85% sucrose solution, which has calculated osmolality and osmolarity values of 5.5 Osmol/kg water and 2.49 Osmol/L of solution, respectively. It is very important to keep this difference in mind when you are given values in either osmolarity or osmolality. In pharmacy practice, osmolarity is used most frequently because we usually make pharmaceutical solutions to a volume, and we can calculate an estimate of osmolarity from the weights of the solutes, their molecular weights, and the expected number of particles per mole for each species. The values obtained from such calculations are only estimates because these calculations assume that the particles behave ideally: Electrolytes completely dissociate and do not interact with each other, and none of the particles self-associate or interact with the water molecules. In reality, solutions, especially concentrated solutions, do not behave ideally.
5. As indicated previously, the concept of osmolarity/osmolality is an important one when dealing with solutions that come in contact with sensitive body tissues.
a. The osmolarity of a solution that is isotonic with body fluids is approximately 0.307 Osmol/L or 307 mOsmol/L.
b. We try to match this osmolarity as closely as possible when we prepare pharmaceutical solutions that are administered parenterally or applied topically to sensitive membranes, such as the eye.
c. For most adults, the lining of the gastrointestinal tract can tolerate highly hypertonic solutions (those of high osmolarity). In contrast, the gastrointestinal lining of neonates is sensitive to hypertonic solutions. Oral solutions for these infants should be close to 300 mOsmol/L (3,4).
6. Because of deviations from ideality, when true effective osmolarity is needed, it should be measured using an appropriate method and instrument. Unfortunately osmolarity cannot be measured directly. Osmometers (instruments that are used in hospitals and laboratories to measure the osmotic properties of biologic fluids and other solutions) measure osmolality rather than osmolarity. It is possible to calculate effective osmolarity from measured osmolality, but you must know (or can measure) the density of the solution and the concentration(s) of the solute(s) in the solution. In this case, the following equation can be used (5).
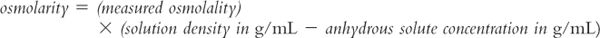
Notice the similarity between this equation and the equation for converting between molarity and molality, which was shown example 8.10. The usefulness of this equation is somewhat limited because in many situations we are dealing with complex solutions containing multiple ingredients. For example, say you are evaluating oral liquid vehicles for use in the neonatal intensive care nursery. The specifications for the manufactured syrup vehicle Ora-Sweet give the osmolality as 3,240 mOsmol/kg. To convert this concentration to osmolarity requires that you have both the density of the syrup and the exact quantities of all the ingredients; while you could measure the density of the syrup, exact formulation ingredient information is not available to you. Fortunately, for most pharmaceutical purposes, we are most interested in an approximate osmolarity because we want to determine whether the solution has an osmolarity close to the desired 300 mOsmol/L of biologic fluids. For the example given earlier, you can easily see that both Ora-Sweet (published osmolality of 3,240 mOsmol/kg) and Syrup NF (calculated osmolarity of 2,490 mOsmol/L) are highly hypertonic and would not be acceptable for use in neonates.
Note: For more precise treatment on the subject of converting between measured osmolality and effective osmolarity, see USP Chapter 〈785〉 Osmolarity and Osmolality.
Examples 8.14 and 8.15 show methods of calculating osmolar concentrations from metric concentrations. 1,000 mOsmol
Calculate milliosmoles per liter from grams per milliliter:
Magnesium sulfate injection is available in a concentration of 50% magnesium sulfate heptahydrate (50 g of MgSO4·7H2O/100 mL). Calculate its concentration in milliosmoles per liter (mOsmol/L). The MW of MgSO4·7H2O = 246.5.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


