Here H₀ is the bioinequivalence hypothesis and H_A is the bioequivalence hypothesis. The values δ_L and δ_U, called the lower and upper bioequivalence limits, are standards set by regulatory agencies that define how ‘close’ the drugs must be to be declared bioequivalent, usually 80%–125%. Obviously, we have δ_L < 1 < δ_U. It may be that δ_U = 1/δ_L. Setting appropriate bioequivalence limits δ_L and δ_U in practice is difficult. It is commonly agreed that they have to be pre-specified and must not be a post-hoc decision, when the data have been analysed. The closer δ_L and δ_U are to 1, the smaller is the difference between test and reference. On the other hand, the closer δ_L and δ_U are to 1, more patients have to be included in the study. Several decision rules are proposed by the US FDA² for setting limits δ_L and δ_U for average bioequivalence testing for example the 80/125 rule, 75/75 rule, 80/20 rule, and the ± 20 rule. For example, for the pharmacokinetic response AUC, for testing hypotheses in Eq. (1), δ_L and δ_U may be set equal to 0.8 and 1.25, respectively. This is the 80/125 rule and generally accepted in other countries as well.³ A good discussion on these rules is also found in Section 1.6 in Chow and Liu.¹ The interval (δ_L, δ_U) is called the equivalence range. Obviously, no two formulations will have identical bioavailability profiles. Therefore, if the profiles of two formulations differ by less than a clinically meaningful limit, the profiles of the two formulations may be considered equivalent. With this in mind, we test the following hypotheses on difference between the means:

(2)

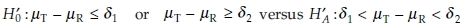
where δ₁ and δ₂ are some clinically meaningful limits. However, this requires the data to be normally distributed. For AUC and C_max, the FDA² recommends logarithmically transforming the data and testing the hypotheses

(3)

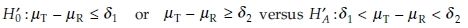
where η_T = log µ_T, η_R = log µ_R, θ_L = log δ_L, and θ_U = log δ_U. As the hypothesis of bioequivalence (H_A) is expressed as an interval, it is then referred to as the interval hypothesis. Westlake⁴ and Schuirmann⁵ introduced the use of interval hypotheses for assessing average bioequivalence. They proposed what is popularly called as the ‘two one-sided tests’ (TOST), which will be used later in this chapter. As stated in Berger and Hsu,⁶ the condition δ_L < µ_T/µ_R = exp (η_T – η_R) < δ_U is equivalent to θ_L < η_T – η_R < θ_U. That is, the hypotheses tested in Eq. (3) can be stated as hypotheses in Eq. (1).

Ratio Hypotheses versus Difference Hypotheses

It is natural and customary to compare the two formulations on the basis of the ratio of the two means. For AUC and C_max, the FDA recommends logarithmically transforming the data and testing hypotheses in Eq. (3). There are two reasons for this recommendation. One reason is that dealing with the ratio of means has been perceived as more difficult than dealing with the difference of means. The second reason is that the untransformed data may not be normal and log transformed data may be normal and better for statistical inference on η_T – η_R. However, these inferences then can be restated in terms of the ratio µ_T/µ_R of means. From a regulatory point of view, as noted by Berger and Hsu,⁶ testing bioequivalence in terms the ratio µ_T/µ_R often reflects clinical rationale rather than the difference µ_T/µ_R. The test of H₀ in Eq. (1) is naturally based on the sample ratio 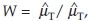which is perceived to be difficult to deal with. Chow and Liu¹ state, ‘It should be noted that the exact distribution of W is rather complicated and is, thus, not trackable’. However, people have overcome this difficulty. Fieller’s theorem enables one to calculate a confidence interval for the ratio of two means. Locke⁷ has proposed an approach for constructing a (1 – 2α) × 100% confidence interval for µ_T/µ_R based on Fieller’s theorem. Recently, Hauschke et al.⁸ have discussed sample size determination for proving equivalence based on the ratio of two means for normally distributed data. Fieller’s theorem approach requires response variables to be normally distributed. As stated in Röhmel,⁹ the construction of confidence interval based on Fieller’s theorem may fail to work occasionally. In this chapter, we propose a statistical test of H₀ in Eq. (1) based on the distribution of the ratio W to assess average bioequivalence. We make inference on µ_T/µ_R directly, and therefore, there is no need for log transformation. Fieller’s theorem approach requires response variables to be normally distributed. Our test procedure requires the sample sizes be large so that the sample means are normally distributed. We describe the test procedure when the data are collected in a crossover design setting.

Crossover Design

In bioavailability/bioequivalence studies, a 2 × 2 crossover design is often used to assess bioequivalence between two formulations (a test formulation and a reference formulation) of a drug product in terms of the extent and rate of absorption of the drug. Under this design, subjects are randomly allocated to two treatment sequences. In sequence 1, subjects receive the test and the reference treatment in periods 1 and 2, respectively. In sequence 2, subjects receive the treatments in reverse order. A sufficiently long washout period between periods is introduced so that carry-over effect is avoided. Let X_ijr and X_ijt denote the bioavailability response of the jth subject ( j = 1, 2, …, n_i) in the ith sequence (i = 1, 2) for the reference formulation and the test formulation, respectively. It is assumed that the covariance matrix of X_ijr and X_ijt is the same for both sequences. Let 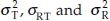denote the variance of X_ijt, the covariance of X_ijr and X_ijt, and the variance of X_ijr, respectively. Let 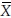_i.r and 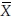_i.t denote the means of bioavailability responses in the ith sequence for the reference formulation and the test formulation, respectively. 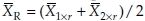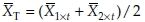Then and are the unbiased estimators of means for the reference and test formulation, respectively. It follows that var 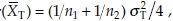and the covariance var 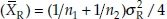and the covariance cov 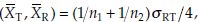We note that the estimates of 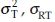and 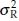are given by

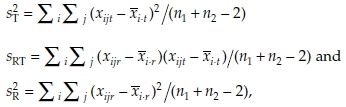
respectively. See Locke⁷ and Hauschke et al.⁸ for further details. In what follows, we set 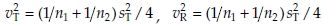and 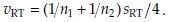We denote the estimated correlation coefficient between 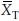and 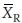as r, where r = v_RT/(v_Tv_R).

New Approach to Bioequivalence Assessment

The objective is to test the null hypothesis in Eq. (1). We propose a new test that depends on what is called the Fieller–Hinkley distribution of the ratio of two normally distributed random variables.

The Fieller-Hinkley distribution is as follows: If 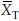and 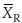are normally distributed with means µ_T and µ_R, variances 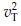and 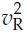, and correlation r, and if P( 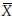_R > 0) → 1, then the distribution of the ratio W = 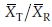is given by

(4)

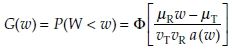
where 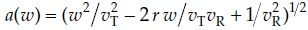and Φ denotes the standard normal distribution function. Note that G can also be written as

(5)

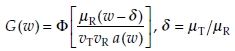
As will be seen later, this distribution function is very easily computed using SAS probnorm function.¹⁰ See Koti¹¹ for further details. Before we discuss the new test procedure, we present a dataset, which will be used throughout this chapter.

Application Data: An Example

Consider the following example, discussed in Chow and Liu,¹ that compares bioavailability between two formulations of a drug product under a standard 2 × 2 crossover design. The study was conducted with 24 healthy volunteers. During each dosing, each subject was administered either five 50-mg tablets (test formulation) or 5 mL of an oral suspension (50 mg/mL; reference formulation). Blood samples were obtained at 0 h before dosing and at various times after dosing. AUC values for 0–32 h, given in Table 19.1 below, were calculated using the trapezoidal method.

Table 19.1. AUC (0-32) for test and reference formulations

Stay updated, free articles. Join our Telegram channel

Join