TERMS
•Percent
•Percent volume-in-volume
•Percent weight-in-volume
•Percent weight-in-weight
•Ratio strength
OBJECTIVES
Upon completion of this chapter, the technician student will be able to:
•Define the three types of percentage preparations.
•Calculate the amount of active ingredient and the amount of inactive ingredient in each of the three types of percentage preparations.
•Define ratio strength.
•Convert ratio strengths to percent strengths and vice versa.
•Calculate the amount of active ingredient in a product using ratio strength.
•Convert percentage concentrations to milligrams per milliliter.
Percentage is an essential part of pharmaceutical calculations. The technician encounters it frequently and uses it as a convenient means of expressing the concentration of an active or inactive material in a pharmaceutical preparation. For example, common expressions are 1% hydrocortisone cream, 0.1% triamcinolone ointment (Fig. 9.1), and a multitude of intravenous solutions, such as 5% dextrose and 0.9% sodium chloride. This chapter explains the various types of percentage preparations and introduces the technician student to calculations involving these products. Many of the calculations in this chapter refer to those relevant to compounding extemporaneous products.
Figure 9.1Examples of percentages used in pharmaceutical preparations.
Percentage and Percentage Preparations
The term percent and its corresponding sign (%) mean by the hundred or in a hundred, and percentage means rate per hundred; so 40% and a percentage of 40 are equivalent expressions. Pharmacy workers most often refer to a percent, not a percentage. A percent may also be expressed as a ratio in a common or decimal fraction. For example, 40% means 40 parts in 100 and may be expressed as 
or 0.4. Percent, therefore, is simply another fraction of such frequent and familiar use that its numerator is expressed but its denominator is understood to be 100.
percent per hundred; or number of parts in each hundred.
For the purposes of computation, percents are usually changed to equivalent decimal fractions. It is much easier mathematically to calculate using a decimal fraction than a ratio. Chapter 1 shows how to convert percents and fractions to decimals. The same methods are used here by dropping the percent sign and dividing the expressed numerator by 100. Thus, 12.5% = 
, or 0.125; and 0.05% = 
, or 0.0005. In the reverse process (changing a decimal to a percent), the decimal is multiplied by 100 and the percent sign is affixed.
The term percent, pharmaceutically speaking, means:
•For solutions or suspensions of solids in liquids, percent weight-in-volume
percent weight-in-volume Measure of a liquid pharmaceutical preparation in grams of solid active ingredient (solute) per 100 mL of the product. It can be applied to solutions, suspensions, lotions, and so on.
•For solutions of liquids in liquids, percent volume-in-volume
percent volume-in-volume Measure of a liquid pharmaceutical preparation in milliliters of active ingredient per 100 mL of the preparation.
•For mixtures of solids or semisolids, percent weight-in-weight
percent weight-in-weight Measure of a pharmaceutical preparation in grams of active ingredient per 100 grams of the preparation.
•For solutions of gases in liquids, percent weight-in-volume
Percentage Weight-in-Volume
In a true expression of percentage (i.e., parts per 100 parts), the percentage of a liquid preparation (e.g., solution, suspension, lotion) would represent the grams of solute or constituent in 100 g of the liquid preparation. However, in practice, the pharmacist most frequently uses a different definition of percentage for solutions and for other liquid preparations, one in which the parts of the percentage represent grams of a solute or constituent in 100 mL of solution or liquid preparation.
Indeed, in weight-in-volume (w/v) expressions, the “correct” strength of a 1% w/v solution or other liquid preparation is defined as containing 1 g of constituent in 100 mL of product. It is assumed that each 100 mL of solution or other liquid preparation weighs 100 g, and that figure is used as the basis for calculating percentage w/v (e.g., 1% w/v = 1% of [100 mL taken to be] 100 g = 1 g in 100 mL).
As with most pharmaceutical calculations, they can be solved in more than one way. No one method is more correct than any other method. Student technicians should be encouraged to become familiar with all methods and to use the method that they best understand.
Weight of Active Ingredient in a Specific Volume, Given Its Percentage Weight-in-Volume
The first method is as follows, taking water to represent any solvent or vehicle and working in the metric system. Multiply the required amount (in milliliters) by the percentage strength, expressed as a decimal, to obtain weight (in grams) of solute or constituent in the solution or liquid preparation. The volume in milliliters represents the weight in grams of the solution or liquid preparation as if it were pure water.
Examples:
How much dextrose (in grams) is required to prepare 4000 mL of a 5% solution?
4000 mL represents 4000 g of solution
5% = 0.05
4000 g × 0.05 = 200 g, answer
Or simply, what is 5% of 4000?
Ratio-proportion is another way to solve this.
A 5% solution contains 5 g in 100 mL. The solution containing 4000 mL must be in the same proportion as the original 5% solution.
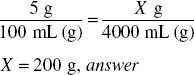
Solve by Dimensional Analysis
How much potassium permanganate (in grams) should be used in compounding the following prescription?
250 ml = 250 g of solution.
0.02% = 0.0002
250 g ×0.0002 = 0.05 g, answer
Or what is 0.02% of 250?
Ratio-proportion is another way to solve this: 0.02% means 0.02 g of potassium permanganate in 100 mL of solution, the solution of 250 mL must be in the same proportion:
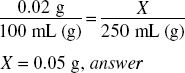
How much aminobenzoic acid (in grams) should be used in preparing 8 fl oz of a 5% solution in 70% alcohol?
8 fl oz = 8 × 30 mL = 240 mL
240 mL represents 240 g of solution.
5% = 0.05
240 g × 0.05 = 12 g, answer
Or simply what is 5% of 240?
We can also solve this using ratio-proportion: 5% means 5 g in 100 mL of solution. The new product with 8 fl oz must be in the same proportion:
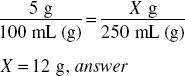
Percentage Weight-in-Volume of Solution, Given Weight of Solute or Constituent and Volume of Solution or Liquid Preparation
For calculation of the percentage w/v of a solution or liquid preparation, given the weight of the solute or constituent and the volume of the solution or liquid preparation, the volume (in milliliters) of the solution represents the weight (in grams) of the solution or liquid preparation as if it were pure water.
Example:
What is the percentage strength w/v of a solution of urea if 80 mL contains 12 g? 80 mL of water weighs 80 g; 80 mL or 80 g = 100% of product. What percent is 12 g?
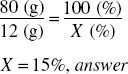
Volume of Solution or Liquid Preparation, Given Percentage Strength Weight-in-Volume and Weight of Solute
Calculating the volume of a solution or liquid preparation, given its percentage strength w/v and the weight of the solute or constituent, entails the following.
Example:
How much (in milliliters) of a 3% solution can be made from 27 g of ephedrine sulfate?
X = 900 g, weight of the solution if it is water.
Volume = 900 mL, answer
Using the ratio-proportion method: 3% means 3 g in 100 mL of solution. The solution containing 27 g must be in the same proportion:
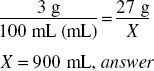
Critical Thinking 9.1
An order was received in the pharmacy. A patient was to receive 50 mg of magnesium sulfate. Magnesium sulfate is available as a 2% w/v product. The pharmacy is in a small rural hospital, and the nursing staff wanted the calculations checked by the pharmacy. The pharmacist was evaluating another critical patient with the physician. The pharmacy technician was registered and certified and had completed an extensive formal training program, and the pharmacist considered the technician competent to check the calculations for the nursing staff. The nurse showed the technician these calculations:
2% = 2 mg/100 mL = 50 mg/X mL
Therefore, to give 50 mg, 100 mL must be used.
Is this amount correct? If not, what error was made?
Review Set 9.1: Percentage Weight-in-Volume
1.What is the percentage strength w/v of solutions using the following amounts of potassium permanganate dissolved in enough purified water to produce 250 mL of solution?
a.25 g
b.50 g
c.5 g
2.How much dextrose (in grams) is in 1 L of 5% dextrose solution?
3.You are to prepare 2 L of a 15% neomycin solution. How much neomycin (in grams) will you need?
4.What volume of a 17% w/v solution contains 1.5 g of active ingredient?
5.What volume of a 20% w/v solution contains 5 g of active ingredient?
6.What volume of a 15% w/v solution contains 7 g of active ingredient?
7.What volume of a 34% w/v solution contains 150 g of active ingredient?
8.How much antipyrine (in grams) should be used in preparing the prescription below?
9.How much tetrahydrozoline hydrochloride (in milligrams) would be used in preparing the prescription below?
10.How much (in milligrams) of a certified red color should be used in preparing 5 L of a 0.01% w/v solution?
11.How much methylparaben (in milligrams) is needed to prepare 8 fl oz of a solution containing 0.12% w/v of methylparaben?
12.How much resin of podophyllum (in grams) should be used in preparing the prescription below?
13.If an injection contains 0.5% w/v of diltiazem hydrochloride, calculate milligrams of the drug in 25 mL of injection.
Percentage Volume-in-Volume
Liquids are usually measured by volume, and the percentage strength indicates the number of parts by volume of the active ingredient in the total volume of the solution or liquid preparation considered as 100 parts by volume. If there is any possibility of misinterpretation, this kind of percentage should be specified as, for example, 10% w/v.
Volume of Active Ingredient in a Specific Volume, Given Percentage Strength Volume-in-Volume
Calculating the volume of the active ingredient in a specified volume of a solution or liquid preparation, given its percentage strength volume-in-volume (v/v), entails the following.
How much liquefied phenol (in milliliters) should be used in compounding the following prescription?
Volume (mL) × %(expressed as a decimal) = milliliters of active ingredient
240 mL × 0.025 = 6 mL, answer
Or simply what is 2.5% of 240?
By ratio-proportion: 2.5% means 2.5 mL of active ingredient in 100 mL of solution. The solution of 240 mL must be in the same proportion:
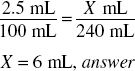
Solve by Dimensional Analysis
