Benjamin K. Poulose and Michael D. Holzman

Introduction

Gastroesophageal reflux disease (GERD) remains one of the most common diseases for which patients seek medical attention. Identifying suitable candidates for surgical management of GERD is a complex process involving documentation of pathologic reflux, assessment of esophageal motility, and discussion of postoperative expectations with patients. The surgical approach to GERD serves to reestablish the original anatomic barriers to reflux, supplemented by fundoplication. The 360-degree fundoplication originally proposed by Rudolph Nissen in the mid-20th century remains the standard by which interventional approaches to GERD are measured.

Surgical Principles

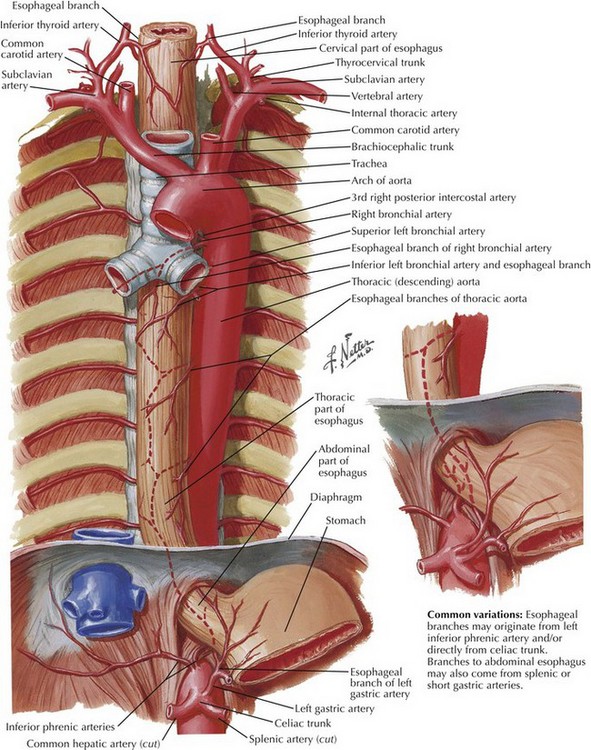
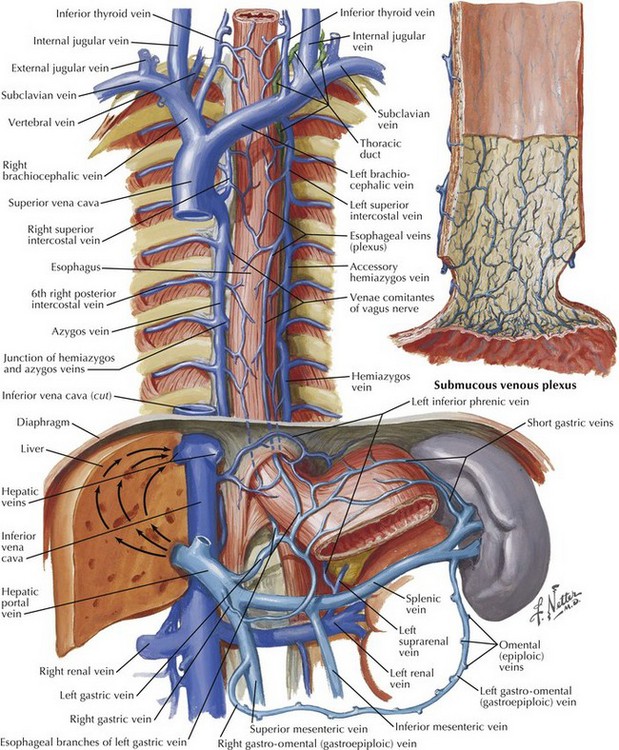
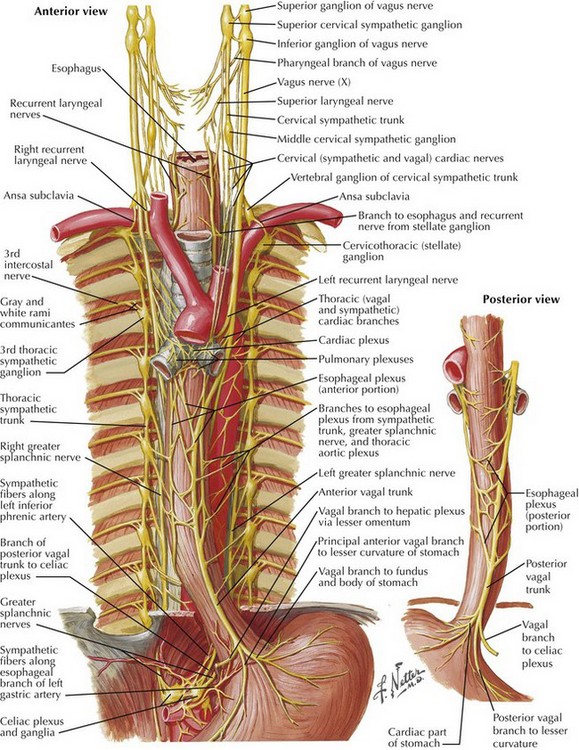
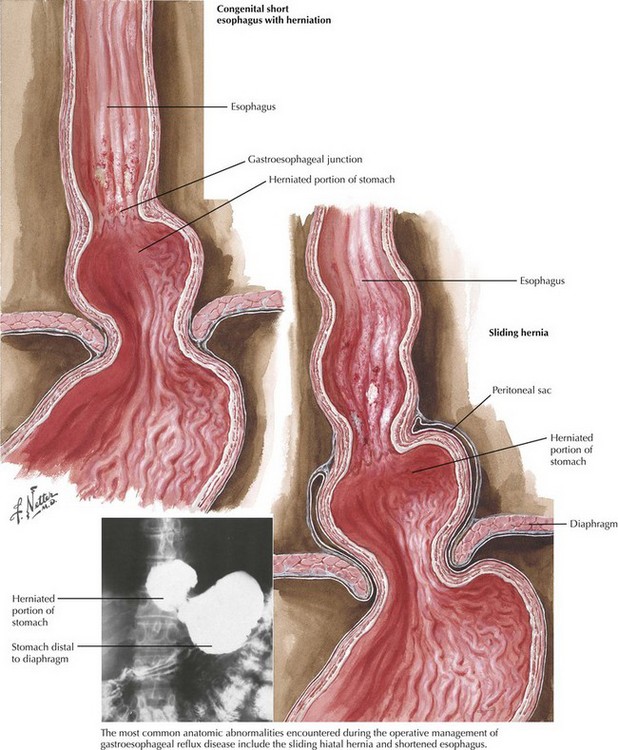
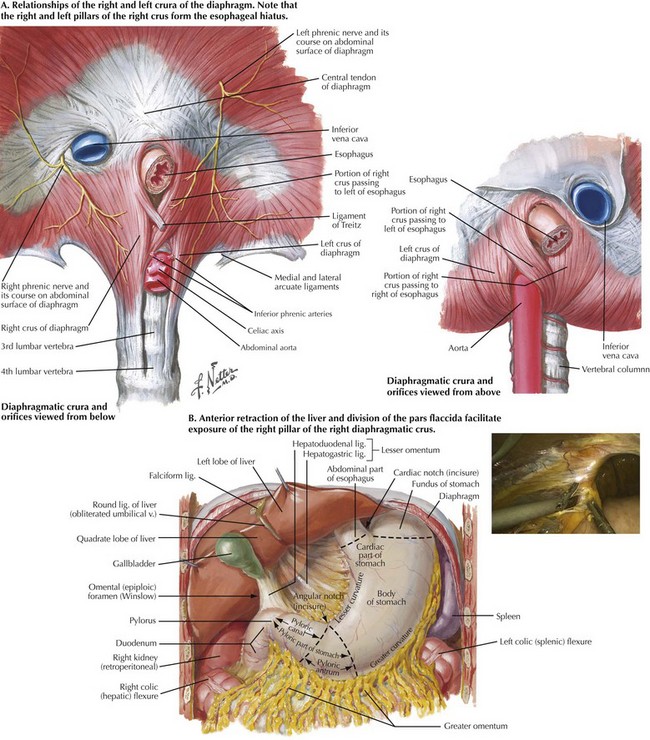
The goals of successful surgical management of GERD are to restore the intraabdominal esophagus, repair the diaphragmatic crura, and reestablish a competent lower esophageal sphincter. A thorough understanding of hiatal anatomy, upper abdominal organ relationships, and mediastinal structures is critical to safe and effective operations for GERD (Figs. 6-1 to 6-3). Restoration of the lower esophageal sphincter is usually accomplished with a “floppy” 360-degree (Nissen) fundoplication formed around the distal esophagus.

Preoperative Studies

Preoperative studies include upper endoscopy, upper gastrointestinal (GI) series, esophageal manometry, and pH testing. Esophageal impedance may help identify patients with pathologic nonacid reflux. Patients with chronic nausea and emesis may benefit from a gastric emptying study to ascertain whether gastroparesis contributes to their symptomatology.

Upper endoscopy can reveal intraluminal pathology that can alter surgical decision making and can help ascertain anatomic changes that would impact the operation for GERD. The most common anatomic abnormality seen in this setting is the sliding, type I hiatal hernia (Fig. 6-4). Upper endoscopy can also reveal a shortened esophagus. The upper GI series also helps define anatomic abnormalities and is useful when more complex hiatal hernias are noted (types II-IV). Testing for acid exposure, nonacid reflux, and assessment of esophageal motility are also important nonimaging modalities that help in preoperative decision making.

Anatomy for Esophageal Mobilization

Adequate esophageal mobilization is important to ensure that sufficient esophagus is present within the abdomen for fundoplication. The end goal of these steps is to confirm at least 4 to 5 cm of esophagus below the diaphragm with circumferential mobilization of the esophagus from surrounding tissues and structures.

Diaphragmatic Crura (Superior and Inferior Views)

In most patients the fibers of the right crus of the diaphragm encircle the esophagus, making the right and left pillars of the right crus the pertinent structures of the esophageal hiatus (Fig. 6-5, A). Abdominal exposure of the right crus is usually obtained by retraction of the left lobe of the liver anteriorly and by incision of the filmy pars flaccida. The right pillar is usually readily identified and bluntly separated from the esophagus (Fig. 6-5, B). If a sizable hiatal hernia is encountered, the plane between the hernia sac and mediastinal structures is developed while preserving healthy endoabdominal fascia overlying the pillars of the crus.

FIGURE 6–5 Anatomy for esophageal mobilization.

Only gold members can continue reading. Log In or Register to continue

Share this:

• Click to share on Twitter (Opens in new window)
• Click to share on Facebook (Opens in new window)

Like this:

Like Loading...

Related

Related posts:

1. Common Bile Duct Surgery and Choledochoduodenostomy
2. Distal Pancreatectomy
3. Abdominoperineal Resection
4. Radical Prostatectomy

Stay updated, free articles. Join our Telegram channel

Join