13 Multivariable Analysis
I Overview of Multivariable Statistics
1. To equalize research groups (i.e., make them as comparable as possible) when studying the effects of medical or public health interventions.
2. To build causal models from observational studies that help investigators understand which factors affect the risk of different diseases in populations (assisting clinical and public health efforts to promote health and prevent disease and injury).
3. To create clinical indices that can suggest the risk of disease in well people or a certain diagnosis, complications, or death in ill people.
Statistical models that have one outcome variable but more than one independent variable are generally called multivariable models (or multivariate models, but many statisticians reserve this term for models with multiple dependent variables).1 Multivariable models are intuitively attractive to investigators because they seem more “true to life” than models with only one independent variable. A bivariate (two-variable) analysis simply indicates whether there is significant movement in Y in tandem with movement in X. Multivariable analysis allows for an assessment of the influence of change in X and change in Y once the effects of other factors (e.g., A, B, and C) are considered.
Multivariable analysis does not enable an investigator to ignore the basic principles of good research design, however, because multivariable analysis also has many limitations. Although the statistical methodology and interpretation of findings from multivariable analysis are difficult for most clinicians, the methods and results are reported routinely in the medical literature.2,3 To be intelligent consumers of the medical literature, health care professionals should at least understand the use and interpretation of the findings of multivariable analysis as usually presented.
II Assumptions Underlying Multivariable Methods
A Conceptual Understanding of Equations for Multivariable Analysis
This statement could be made to look more mathematical simply by making a few slight changes:
The four independent variables on the right side of the equation are almost certainly not of exactly equal importance. Equation 13-2 can be improved by giving each independent variable a coefficient, which is a weighting factor measuring its relative importance in predicting prognosis. The equation becomes:
Before equation 13-3 can become useful for estimating survival for an individual patient, two other factors are required: (1) a measure to quantify the starting point for the calculation and (2) a measure of the error in the predicted value of y for each observation (because statistical prediction is almost never perfect for a single individual). By inserting a starting point and an error term, the ≈ symbol (meaning “varies with”) can be replaced by an equal sign. Abbreviating the weights with a W, the equation now becomes:
Although equation 13-5 looks complex, it really means the same thing as equations 13-1 through 13-4.
B Best Estimates
This equation is true because 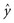 is only an estimate, which can have error. When equation 13-6 is subtracted from equation 13-5, the following equation for the error term emerges:
is only an estimate, which can have error. When equation 13-6 is subtracted from equation 13-5, the following equation for the error term emerges:
In straightforward language, the best estimates for the values of a and b1 through bi are found when the total quantity of error (measured as the sum of squares of the error term, or most simply e2) has been minimized. The values of a and the several bs that, taken together, give the smallest value for the squared error term (squared for reasons discussed in Chapter 9) are the best estimates that can be obtained from the set of data. Appropriately enough, this approach is called the least-squares solution because the process is stopped when the sum of squares of the error term is the least.
C General Linear Model
The multivariable equation shown in equation 13-6 is usually called the general linear model. The model is general because there are many variations regarding the types of variables for y and xi and the number of x variables that can be used. The model is linear because it is a linear combination of the xi terms. For the xi variables, a variety of transformations might be used to improve the model’s “fit” (e.g., square of xi, square root of xi, or logarithm of xi). The combination of terms would still be linear, however, if all the coefficients (the bi terms) were to the first power. The model does not remain linear if any of the coefficients is taken to any power other than 1 (e.g., b2). Such equations are much more complex and are beyond the scope of this discussion.
Numerous procedures for multivariable analysis are based on the general linear model. These include methods with such imposing designations as analysis of variance (ANOVA), analysis of covariance (ANCOVA), multiple linear regression, multiple logistic regression, the log-linear model, and discriminant function analysis. As discussed subsequently and outlined in Table 13-1, the choice of which procedure to use depends primarily on whether the dependent and independent variables are continuous, dichotomous, nominal, or ordinal. Knowing that the procedures listed in Table 13-1 are all variations of the same theme (the general linear model) helps to make them less confusing. Detailing these methods is beyond the scope of this text but readily available both online* and in print.4
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


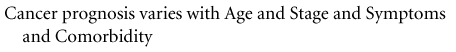 (13-1)
(13-1)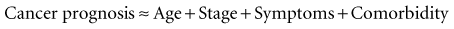 (13-2)
(13-2)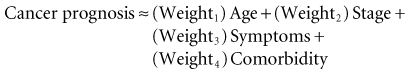 (13-3)
(13-3) (13-4)
(13-4)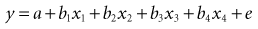 (13-5)
(13-5)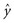 ). If the values of all the observed ys and xs are inserted, the following equation can be solved:
). If the values of all the observed ys and xs are inserted, the following equation can be solved: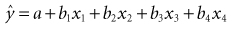 (13-6)
(13-6)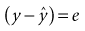 (13-7)
(13-7)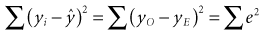 (13-8)
(13-8)
