Figure 3.1 Drug label for Tagamet. (Courtesy of GlaxoSmithKline.)
Mathematical Ability
Nurses find that mathematical calculations are performed using various methods to prepare drugs for administration. Sometimes the math is relatively simple, and a calculation can be done quickly in one’s head. When distractions are present or if conversions are involved, the nurse may use a pen and paper to handwrite out the mathematical equations needed to determine the correct dose. A nurse may use a number of steps in the calculation of a medication and find that a calculator is helpful to hasten the process. When using any of these methods, it is important for the nurse to understand the basic concepts of the dose calculation to ensure the right answer is obtained.
In the remainder of this chapter a variety of calculation methods are presented. Try the calculations with the different formulas to discover the best way you calculate drug doses. See Appendix F for a review of basic mathematical concepts if you have difficulty understanding the math involved with the calculations.
Basic Formula Method of Dosage Calculation
Once the nurse has identified the basic information about the drug, the calculation can be performed to prepare the drug.
CALCULATION #1
Looking at the label in Figure 3.1, use this information to solve the following dose problem:
The primary health care provider orders: 400 mg of cimetidine after each meal. How many tablets will the nurse administer following breakfast? (See Appendix G for answer.)
Although most hospital pharmacies dispense drugs as single doses or in a unit dose system, on occasion you must compute a drug dosage because it differs from the dose of the drug that is available. This is particularly true of long-term care facilities, of outpatient clinics, and in the home where the dose may be changed periodically or in situations in which having multiple dosage strengths of a particular drug for the patient would be costly.
CALCULATION #2
Looking at the label in Figure 3.1, use this information to solve the following dose problem:
The primary health care provider changes the order after late morning rounds: 800 mg of cimetidine after each meal. How many tablets will the nurse administer after meals? (See Appendix G for answer.)
Some nurses can do this type of calculation in their heads; others find it helpful to do the problem by hand on paper. This is especially helpful when the dosage ordered by the primary health care provider may not be available.
Basic Formula Method by Hand
To find the correct dosage of a solid oral preparation, the following formula may be used:
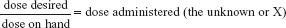
This formula may be abbreviated as:
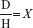
When the dose ordered by the primary health care provider (dose desired) is written in the same measurement as the dose on the drug container (dose on hand) (e.g., they are both milligrams), then these two figures may be inserted into the formula without changes.
EXAMPLE
The primary health care provider orders cimetidine 800 mg (milligrams). The drug is available as cimetidine 400 mg (milligrams).
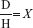
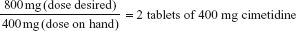

Figure 3.2 Drug label for Zyprexa. (Courtesy of Lilly Company.)
QUESTION #3
Use the label in Figure 3.2 to solve the following problem.
Looking at the label, find the drug name, form, and dosage strength. (See Appendix G for answer.)
CALCULATION #3
Looking at the label in Figure 3.2, use this information to solve the following dose problem:
The primary health care provider orders: 10 mg Zyprexa daily. How many tablets will the nurse administer? (See Appendix G for answer.)
Understanding the Metric System of Measurement
If the primary health care provider orders ascorbic acid (vitamin C) 0.5 g, and the drug container label reads ascorbic acid 250 mg, a conversion of grams to milligrams (because the drug container is labeled in milligrams) would be necessary before the basic formula can be used. Therefore, it is important for the nurse to understand the metric system of measurement.
There are three systems of measurement associated with drug dosing: (1) the metric system, (2) the apothecary system, and (3) household measurements.
The metric system is the most commonly used system of measurement in medicine. The metric system uses decimals (or the decimal system). In the metric system, the gram is the unit of weight, the liter the unit of volume, and the meter the unit of length. Display 3.1 lists the measurements used in the metric system. The abbreviations for the measurements are given in parentheses.
The apothecary system at one time was used for weight measurement. In 1994, recommendations were made by the Institute for Safe Medication Practices (ISMP) to eliminate this system due to the high rate of medication errors it produced (information about this system can be found in Appendix F). The household system is rarely used in a hospital setting but may be used to measure drug dosages in the home.
Display 3.1 Metric Measurements
Weight
The unit of weight is the gram.
1 kilogram (kg) = 1000 grams (g)
1 gram (g) = 1000 milligrams (mg)
1 milligram (mg) = 1000 micrograms (mcg)
Volume
The unit of volume is the liter.
1 deciliter (dL) = 10 liters (L)
1 liter (L) = 1000 milliliters (mL)
1 milliliter (mL) = 0.001 liter (L)
Length
The unit of length is the meter.
1 meter (m) = 100 centimeters (cm)
1 centimeter (cm) = 0.01 meter (m)
1 millimeter (mm) = 0.001 meter (m)
Ratio and Proportion Method of Dosage Calculation
Converting Units for Calculation
When using the basic formula, the numerator and the denominator must be of like terms—for example, milligrams over milligrams or grams over grams. To set up a problem, a fraction must be stated in like terms; therefore, proportion may be used to convert grams to milligrams.
 NURSING ALERT
NURSING ALERT
Errors made by nurses in using this and other drug formulas will be reduced if the entire dose is labeled rather than just writing the numbers.

This will eliminate the possibility of using unlike terms in the fraction.
In the aforementioned example, where the order read ascorbic acid 0.5 g and the drug container was labeled ascorbic acid 250 mg, a conversion of grams to milligrams is necessary to perform the dose calculation. A nurse may be able to perform this calculation without writing it down. If it is done by hand, the proportion and a known equivalent are set up in a ratio and used for this type of conversion.
Ratio and Proportion Method by Hand
EXAMPLE
Convert 0.5 gram (g) to milligrams (mg); using proportion and the known equivalent 1000 mg = 1 g, set up the ratio:
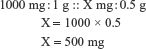

Figure 3.3 Drug label for Lanoxin. (Courtesy of GlaxoSmithKline.)
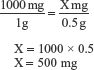
Therefore, 0.5 gram (g) equals 500 milligrams (mg). After changing 0.5 g to 500 mg, use the basic method formula:
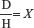
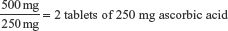
Safeguard in Preventing Errors
To prevent dose calculation errors, many manufacturers include both levels of measurement (grams and milligrams) on the label if the drug is frequently ordered in doses different from the size dispensed (Fig. 3.3). This is very important when doses are in small amounts such as micrograms (mcg). Again, manufacturers typically include the dose strength in both units of measurement (milligrams and micrograms). Even when both are included, the nurse should perform the calculation to double check that the dose is correct.
Errors are a frequent problem when zeros (0) are involved. When there is no number to the left of the decimal, a zero is written, for example, 0.25. Although in general mathematics the zero may not be required, it should be used in the writing of all drug doses. Use of the zero lessens the chance of drug errors, especially when the dose of a drug is hurriedly written and the decimal point is indistinct.
For example, if a drug order is written as digoxin (Lanoxin) .25 mg instead of digoxin 0.25 mg, the order might be interpreted as 25 mg, which is 100 times the prescribed dose.
QUESTION #4
Use the label in Figure 3.3 to understand the following example.
Looking at the label, find the drug name, form, and dosage strength in both units of measurement. (See Appendix G for answer.)
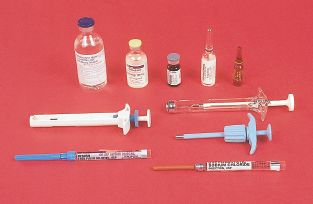
Figure 3.4 Drug preparations in solution form: (top row) vials and ampules; (middle/bottom rows) prefilled cartridges and holders.
CALCULATION #4
Looking at the label in Figure 3.3, use this information to solve the following dose problem:
The primary health care provider orders: 0.50 mg of digoxin daily. How many tablets will the nurse administer? (See Appendix G for answer.)
Drugs in Liquid Form
Drugs may be ordered in liquid form for many reasons: The patient is a child, the drug is to be put in a feeding tube or injected directly into the tissues or intravenous (IV) line, or the patient is too ill to swallow a solid form of the drug like a tablet. In these situations, the drug is made in a solution form.
Solutions
A solute is a substance dissolved in a solvent to make a solution. Usually, water is used as the solvent for preparing a solution unless another liquid is specified. Today, most solutions are prepared by a clinical pharmacist or the manufacturer and not by the nurse. It is important for the nurse to understand how the solutions will be prepared and labeled.

Figure 3.5 Drug label for Augmentin. (Courtesy of GlaxoSmithKline.)
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


