CHAPTER 5 Generation and Conduction of Action Potentials
An action potential is a rapid, all-or-none change in the membrane potential followed by a return to the resting membrane potential.
MEMBRANE POTENTIALS
Observations of Membrane Potentials
All cells, including neurons, have a resting potential that is typically around −70 mV, as detailed in Chapter 1. One of the signature features of neurons is their ability to change their membrane potential rapidly in response to an appropriate stimulus, and the most significant of these responses is the action potential. Our current knowledge about the ionic mechanisms of action potentials comes from experiments with many species. One of the most studied, however, is the squid because the large diameter (up to 0.5 mm) of the squid giant axon makes it a convenient model for electrophysiological research with intracellular electrodes. When a microelectrode (tip diameter <0.5 μm) is inserted through the plasma membrane of the squid giant axon, a potential difference is observed between the tip of the microelectrode inside the cell and an electrode placed outside the cell. The internal electrode is approximately 70 mV negative with respect to the external electrode. This 70-mV potential difference is the resting membrane potential of the axon. By convention, membrane potentials are expressed as the intracellular potential minus the extracellular potential; therefore, the resting potential of squid giant axons, as well as many mammalian neurons, is about −70 mV. In the absence of perturbing influences, the resting membrane potential remains at −70 mV.
The Passive Response
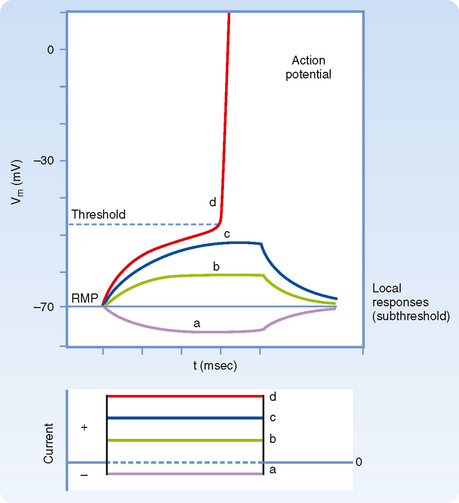
Figure 5-1 illustrates the results of an experiment in which the membrane potential of an axon is perturbed by passing rectangular pulses of depolarizing or hyperpolarizing current across the plasma membrane. The injection of positive charge, which changes the membrane potential from −70 mV to −60 mV, is depolarizing because it makes the cell more positive (i.e., decreases the potential difference across the cell membrane). Conversely, a change in the membrane potential from −70 mV to −80 mV as a result of the injection of negative charge increases the polarization of the membrane; this change in potential is called hyperpolarization. The more current that passes across the plasma membrane, the larger the change in the membrane potential.
Note that although the current is injected as rectangular pulses, with vertical rising and falling edges, the shape of the membrane response to smallamplitude current pulses has a slower rise and fall. For hyperpolarizing and small-amplitude depolarizing current pulses, the rise and fall in the membrane voltage response has an exponential shape because the membrane is responding to the current as would a passive RC circuit. That is, the stimulus causes no change in membrane resistance or capacitance, and thus the time course of the rise and fall simply reflects the time required to discharge or charge the membrane capacitance. Recall that because there is an excess of negative ions inside the axon in comparison to outside, those negative ions will attract some positive ions to the outside of the membrane. These charges remain separated from each other by the cell membrane, similar to the storage of charge in a capacitor. Thus, at least in this passive domain, the membrane response to electrical stimuli closely follows the same laws that govern an electric circuit composed of a resistor and capacitor connected in parallel.
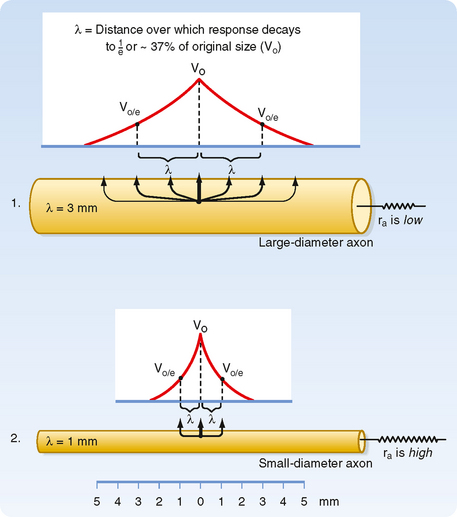
When current pulses that elicit only passive responses are passed across the plasma membrane, the size of the potential change recorded depends on the distance of the recording electrode from the point of passage of the current (Fig. 5-2). The closer the recording electrode to the site of current passage, the larger and steeper the potential change. The magnitude of the potential change decreases exponentially with distance from the site of passage of the current, and the potential change is said to reflect passive or electrotonic conduction. Such changes do not spread very far along the membrane before they become insignificant. As shown in Figure 5-2, an electrotonically conducted signal dies away over a distance of a few millimeters. The distance over which the potential change decreases to 1/e (37%) of its maximal value is called the length constant or space constant (e is the base of natural logarithms and is equal to 2.7182). A length constant of 1 to 3 mm is typical for mammalian axons.
Based on cable theory, the length constant can be related to axonal resistance and is equal to 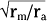 . By using this relationship we can determine how changes in axonal diameter will affect the length constant and hence how the decay of electrotonic potentials will vary. An increase in diameter of the axon will reduce both ra and rm. However, rm is inversely proportional to diameter (because it is related to the circumference of the axon), whereas ra varies inversely to the diameter squared (because it is related to the cross-sectional area of the axon). Thus, radecreases more rapidly than rm does as axonal diameter increases, and therefore the length constant increases (Fig. 5-3).
. By using this relationship we can determine how changes in axonal diameter will affect the length constant and hence how the decay of electrotonic potentials will vary. An increase in diameter of the axon will reduce both ra and rm. However, rm is inversely proportional to diameter (because it is related to the circumference of the axon), whereas ra varies inversely to the diameter squared (because it is related to the cross-sectional area of the axon). Thus, radecreases more rapidly than rm does as axonal diameter increases, and therefore the length constant increases (Fig. 5-3).
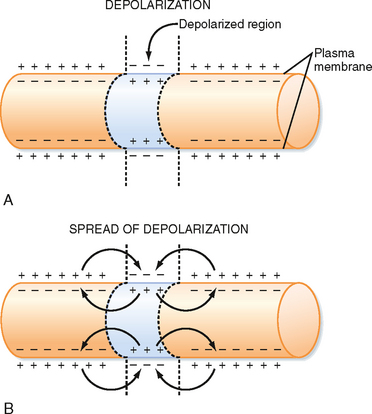
Membrane capacitance is a major factor that shapes the time course of passive responses. To depolarize an adjacent portion of axon, the injected depolarizing positive charges must draw the inner negative charges from the membrane and thereby free the external positive charges (Fig. 5-4). The time that this process takes increases with the amount of axon membrane to be depolarized.
The Local (Subthreshold) Response
If a somewhat larger depolarizing current pulse is applied to a small portion of the membrane of an axon (Fig. 5-1, c), the voltage response no longer looks like that of a passive RC circuit (e.g., the tail does not decay exponentially). The shape is altered because the stimulus has changed the membrane potential sufficiently to cause the opening of significant numbers of voltage-sensitive Na+ channels (see later). Opening of these channels changes the membrane’s resistance and allows Na+ to enter, driven by its electrochemical gradient. This entry of positive charge enhances the depolarization by adding to the current pulse. The resulting depolarization is called a local or subthreshold response. The local response results from active changes in membrane properties (specifically rm), which distinguishes it from the passive electrotonic response. Nevertheless, it is not self-regenerating and does not propagate down the axon but, again, decreases in amplitude with distance. The change in membrane properties is insufficient for what is needed to generate an action potential.
SUPRATHRESHOLD RESPONSE: THE ACTION POTENTIAL
Somewhat larger local responses are observed with still larger depolarizing current pulses until a threshold membrane potential is reached at which a different sort of response, the action potential (or spike), occurs (Fig. 5-5; see also Fig. 5-1, d). For example, the threshold value for the squid giant axon is near −55 mV. When the membrane potential exceeds this value, an action potential is triggered. Thus, the threshold can be defined as the membrane voltage at which there is a 50 : 50 chance of generating an action potential.
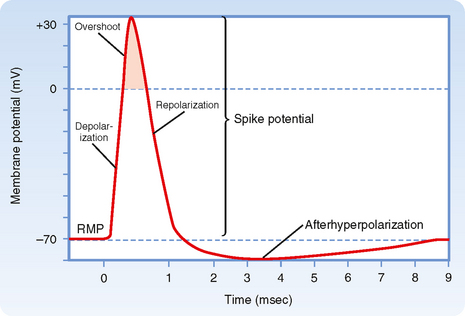
Action potentials can be generated in other parts of the nerve cell membrane, but their most prominent role is signal conduction along the axon. When the membrane is depolarized to threshold, the depolarization becomes explosive (Fig. 5-5). The depolarization completely depolarizes the membrane and even overshoots such that the membrane potential reverses from negative to positive. The peak of the action potential approaches +50 mV. The membrane potential then returns toward the resting membrane potential almost as rapidly as it was depolarized. After repolarization, a variable hyperpolarization occurs that is known as the afterhyperpolarization. The action potential’s depolarization has a duration of 1 to 2 msec, but the hyperpolarizing afterpotential can persist from a few to 100 msec, depending on the particular type of neuron.
Ionic Basis of Action Potentials
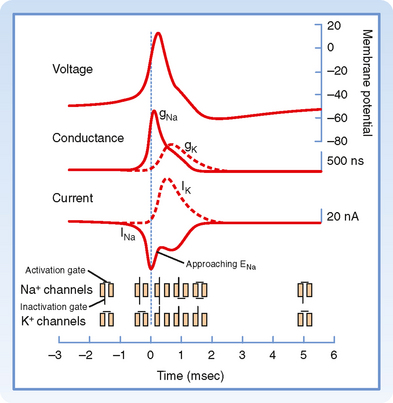
An action potential is the result of successive, rapid, and transient changes in plasma membrane conductance to sodium and potassium ions. In the squid giant axon, the resting membrane potential (Vm) is about −70 mV, and the equilibrium potential of K+ (EK) is about −100 mV. An increase in gK would therefore hyperpolarize the membrane, whereas a decrease in gK would tend to depolarize the membrane (see Chapter 2). Conversely, an increase in gNa would cause depolarization and, if of sufficient magnitude, even a reversal in membrane polarity because ENa is about +65 mV in the squid giant axon.
As with the resting membrane potential, the action potential depends on the opposing tendencies of (1) the Na+ gradient to bring the resting membrane potential toward the equilibrium potential for Na+ and (2) the K+ gradient to bring the resting membrane potential toward the equilibrium potential for K+. The relationship between potential, conductance, and ion current during an action potential includes the following (Fig. 5-6):
Ion Channels and Gates
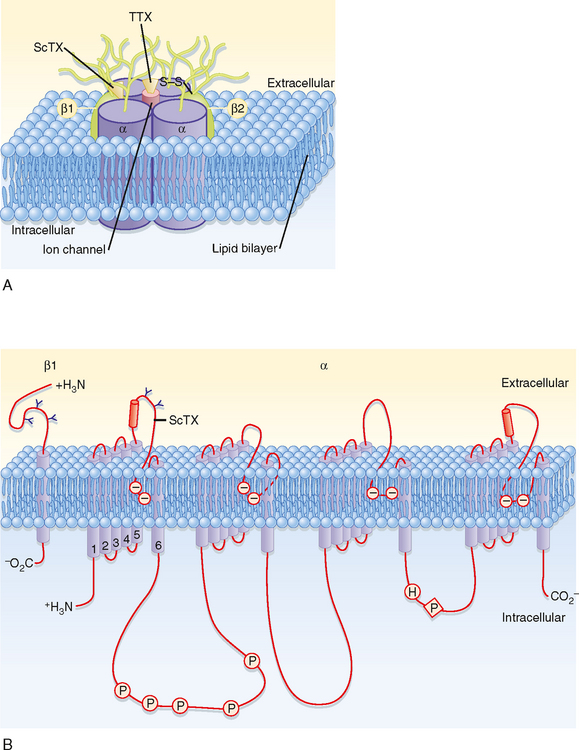
The structure of a voltage-gated Na+ channel (Fig. 5-7) consists of a single α subunit in association with a β1 and a β2 subunit. The α subunit has four repeated motifs of six transmembrane helices that surround a central ion channel or pore. The channel’s walls are partly formed by the number 6 helices in each motif. The functional channels of most voltage-gated K+ channels are comprised of four separate subunits, each consisting of a polypeptide with six membrane-spanning segments and similar to the motifs which make up the single α subunit of the Na+ channel.
Another important characteristic of some channels such as those that underlie the action potential is that they are gated by change in voltage (i.e., they are voltage-gated channels). The gates sense the potential across the membrane and then act to either open or close the channel according to the membrane potential. The gates are formed by groups of charged amino acid residues, and the voltage dependence of the Na+ and K+ channel gates can account for the complex changes in gNa and gK that occur during an action potential.
Behavior of Individual Ion Channels during the Action Potential
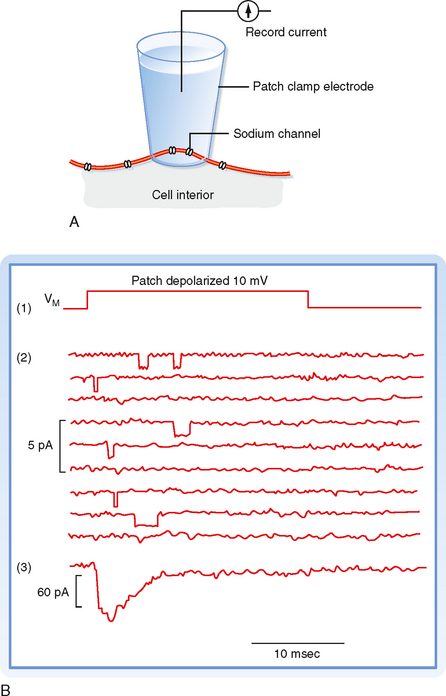
One way to study the behavior of individual ion channels and how they contribute to the membrane potential is to incorporate either purified ion channel proteins or bits of nerve membrane into planar lipid bilayers separating two aqueous compartments. Electrodes placed in the aqueous compartments can then be used to monitor or impose currents and voltages across the membrane. Another way to study individual ion channels involves the use of patch electrodes. A fire-polished microelectrode is placed against the surface of a cell, and suction is applied to the electrode. A high-resistance seal is formed around the tip of the electrode (Fig. 5-8, A). The sealed patch electrodecan then be used to monitor the activity of whatever channels happen to be trapped inside the seal. Under ideal conditions only one or only a few ion channels of a single type may be present in either the planar membrane or the membrane patch. The ion channels spontaneously oscillate between conductance states: an open state and a closed state. In the case of voltage-gated channels, the time spent in a particular state will be a probabilistic function of the membrane potential.
< div class='tao-gold-member'>
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree