OBJECTIVES
After studying this chapter, you should be able to:
Define units used in measuring physiologic properties.
Define pH and buffering.
Understand electrolytes and define diffusion, osmosis, and tonicity.
Define and explain the significance of resting membrane potential.
Understand in general terms the basic building blocks of the cell: nucleotides, amino acids, carbohydrates, and fatty acids.
Understand higher-order structures of the basic building blocks: DNA, RNA, proteins, and lipids.
Understand the basic contributions of the basic building blocks to cell structure, function, and energy balance.
INTRODUCTION
In unicellular organisms, all vital processes occur in a single cell. As the evolution of multicellular organisms progressed, various cell groups organized into tissues and organs have taken over particular functions. In humans and other vertebrate animals, the specialized cell groups include a gastrointestinal system to digest and absorb food; a respiratory system to take up O2 and eliminate CO2; a urinary system to remove wastes; a cardiovascular system to distribute nutrients, O2, and the products of metabolism; a reproductive system to perpetuate the species; and nervous and endocrine systems to coordinate and integrate the functions of the other systems. This book is concerned with the way these systems function and the way each contributes to the functions of the body as a whole. This first chapter focuses on a review of basic biophysical and biochemical principles and the introduction of the molecular building blocks that contribute to cellular physiology.
GENERAL PRINCIPLES
The cells that make up the bodies of all but the simplest multicellular animals, both aquatic and terrestrial, exist in an “internal sea” of extracellular fluid (ECF) enclosed within the integument of the animal. From this fluid, the cells take up O2 and nutrients; into it, they discharge metabolic waste products. The ECF is more dilute than present-day seawater, but its composition closely resembles that of the primordial oceans in which, presumably, all life originated.
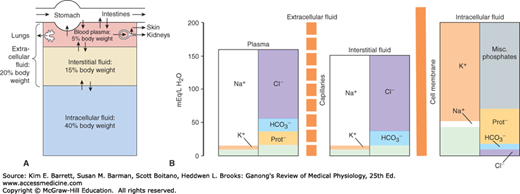
In animals with a closed vascular system, the ECF is divided into the interstitial fluid, the circulating blood plasma, and the lymph fluid that bridges these two domains. The plasma and the cellular elements of the blood, principally red blood cells, fill the vascular system, and together they constitute the total blood volume. The interstitial fluid is that part of the ECF that is outside the vascular and lymph systems, bathing the cells. About one-third of the total body water is extracellular; the remaining two-thirds is intracellular (intracellular fluid). Inappropriate compartmentalization of the body fluids can result in edema (Clinical Box 1–1). In the average young adult male, 18% of the body weight is protein and related substances, 7% is mineral, and 15% is fat. The remaining 60% is water. The distribution of this water is shown in Figure 1–1A.
FIGURE 1–1
Organization of body fluids and electrolytes into compartments. A) Body fluids can be divided into intracellular and extracellular fluid compartments (ICF and ECF, respectively). Their contribution to percentage body weight (based on a healthy young adult male; slight variations exist with age and gender) emphasizes the dominance of fluid makeup of the body. Transcellular fluids, which constitute a very small percentage of total body fluids, are not shown. Arrows represent fluid movement between compartments. B) Electrolytes and proteins are unequally distributed among the body fluids. This uneven distribution is crucial to physiology. Prot–, protein, which tends to have a negative charge at physiologic pH.
CLINICAL BOX 1–1 Edema
Edema is the build up of body fluids within tissues. The increased fluid is related to an increased leak from the blood and/or reduced removal by the lymph system. Edema is often observed in the feet, ankles, and legs, but can happen in many areas of the body in response to disease, including those of the heart, lung, liver, kidney, or thyroid.
THERAPEUTIC HIGHLIGHTSThe best treatment for edema includes reversing the underlying disorder. Thus, proper diagnosis of the cause of edema is the primary first step in therapy. More general treatments include restricting dietary sodium to minimize fluid retention and using appropriate diuretic therapy.
The intracellular component of the body water accounts for about 40% of body weight and the extracellular component for about 20%. Approximately 25% of the extracellular component is in the vascular system (plasma = 5% of body weight) and 75% outside the blood vessels (interstitial fluid = 15% of body weight). The total blood volume is about 8% of body weight. Flow between these compartments is tightly regulated.
In considering the effects of various physiologically important substances and the interactions between them, the number of molecules, electrical charges, or particles of a substance per unit volume of a particular body fluid are often more meaningful than simply the weight of the substance per unit volume. For this reason, physiologic concentrations are frequently expressed in moles, equivalents, or osmoles.
A mole is the gram-molecular weight of a substance, that is, the molecular weight of the substance in grams. Each mole (mol) consists of 6 × 1023 molecules. The millimole (mmol) is 1/1000 of a mole, and the micromole (μmol) is 1/1,000,000 of a mole. Thus, 1 mol of NaCl = 23 g + 35.5 g = 58.5 g and 1 mmol = 58.5 mg. The mole is the standard unit for expressing the amount of substances in the SI unit system.
The molecular weight of a substance is the ratio of the mass of one molecule of the substance to the mass of one-twelfth the mass of an atom of carbon-12. Because molecular weight is a ratio, it is dimensionless. The dalton (Da) is a unit of mass equal to one-twelfth the mass of an atom of carbon-12. The kilodalton (kDa = 1000 Da) is a useful unit for expressing the molecular mass of proteins. Thus, for example, one can speak of a 64-kDa protein or state that the molecular mass of the protein is 64,000 Da. However, because molecular weight is a dimensionless ratio, it is incorrect to say that the molecular weight of the protein is 64 kDa.
The concept of electrical equivalence is important in physiology because many of the solutes in the body are in the form of charged particles. One equivalent (Eq) is 1 mol of an ionized substance divided by its valence. One mole of NaCl dissociates into 1 Eq of Na+ and 1 Eq of Cl–. One equivalent of Na+ = 23 g, but 1 Eq of Ca2+ = 40 g/2 = 20 g. The milliequivalent (mEq) is 1/1000 of 1 Eq.
Electrical equivalence is not necessarily the same as chemical equivalence. A gram equivalent is the weight of a substance that is chemically equivalent to 8.0 g of oxygen. The normality (N) of a solution is the number of gram equivalents in 1 L. A 1 N solution of hydrochloric acid contains both H+ (1.0 g) and Cl– (35.5 g) equivalents, = (1.0 g + 35.5 g)/L = 36.5 g/L.
The water molecule (H2O) is an ideal solvent for physiologic reactions. H2O has a dipole moment where oxygen slightly pulls away electrons from the hydrogen atoms and creates a charge separation that makes the molecule polar. This allows water to dissolve a variety of charged atoms and molecules. It also allows the H2O molecule to interact with other H2O molecules via hydrogen bonding. The resulting hydrogen bond network in water allows for several key properties relevant to physiology: (1) water has a high surface tension, (2) water has a high heat of vaporization and heat capacity, and (3) water has a high dielectric constant. In layman’s terms, H2O is an excellent biologic fluid that serves as a solute; it provides optimal heat transfer and conduction of current.
Electrolytes (eg, NaCl) are molecules that dissociate in water to their cation (Na+) and anion (Cl–) equivalents. Because of the net charge on water molecules, these electrolytes tend not to reassociate in water. There are many important electrolytes in physiology, notably Na+, K+, Ca2+, Mg2+, Cl–, and HCO3–. It is important to note that electrolytes and other charged compounds (eg, proteins) are unevenly distributed in the body fluids (Figure 1–1B). These separations play an important role in physiology.
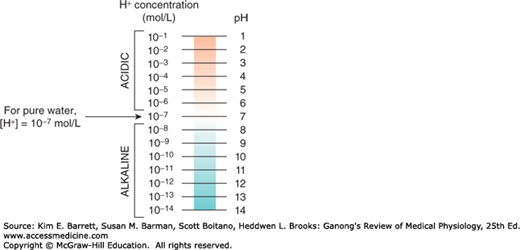
The maintenance of a stable hydrogen ion concentration ([H+]) in body fluids is essential to life. The pH of a solution is defined as the logarithm to the base 10 of the reciprocal of the H+, that is, the negative logarithm of the [H+]. The pH of water at 25°C, in which H+ and OH– ions are present in equal numbers, is 7.0 (Figure 1–2). For each pH unit less than 7.0, the [H+] is increased 10-fold; for each pH unit above 7.0, it is decreased 10-fold. In the plasma of healthy individuals, pH is slightly alkaline, maintained in the narrow range of 7.35–7.45 (Clinical Box 1–2). Conversely, gastric fluid pH can be quite acidic (on the order of 3.0) and pancreatic secretions can be quite alkaline (on the order of 8.0). Enzymatic activity and protein structure are frequently sensitive to pH; in any given body or cellular compartment, pH is maintained to allow for maximal enzyme/protein efficiency.
Molecules that act as H+ donors in solution are considered acids, while those that tend to remove H+ from solutions are considered bases. Strong acids (eg, HCl) or bases (eg, NaOH) dissociate completely in water and thus can most change the [H+] in solution. In physiologic compounds, most acids or bases are considered “weak,” that is, they contribute or remove relatively few H+ from solution. Body pH is stabilized by the buffering capacity of the body fluids. A buffer is a substance that has the ability to bind or release H+ in solution, thus keeping the pH of the solution relatively constant despite the addition of considerable quantities of acid or base. Of course there are a number of buffers at work in biologic fluids at any given time. All buffer pairs in a homogenous solution are in equilibrium with the same [H+]; this is known as the isohydric principle. One outcome of this principle is that by assaying a single buffer system, we can understand a great deal about all of the biologic buffers in that system.
CLINICAL BOX 1–2 Acid–Base Disorders
Excesses of acid (acidosis) or base (alkalosis) exist when the blood is outside the normal pH range (7.35–7.45). Such changes impair the delivery of O2 to and removal of CO2 from tissues. There are a variety of conditions and diseases that can interfere with pH control in the body and cause blood pH to fall outside of healthy limits. Acid–base disorders that result from respiration to alter CO2 concentration are called respiratory acidosis and respiratory alkalosis. Nonrespiratory disorders that affect HCO3– concentration are referred to as metabolic acidosis and metabolic alkalosis. Metabolic acidosis or alkalosis can be caused by electrolyte disturbances, severe vomiting or diarrhea, ingestion of certain drugs and toxins, kidney disease, and diseases that affect normal metabolism (eg, diabetes).
THERAPEUTIC HIGHLIGHTSProper treatments for acid–base disorders are dependent on correctly identifying the underlying causal process(es). This is especially true when mixed disorders are encountered. Treatment of respiratory acidosis should be initially targeted at restoring ventilation, whereas treatment for respiratory alkalosis is focused on the reversal of the root cause. Bicarbonate is typically used as a treatment for acute metabolic acidosis. An adequate amount of a chloride salt can restore acid–base balance to normal over a matter of days for patients with a chloride-responsive metabolic alkalosis whereas chloride-resistant metabolic alkalosis requires treatment of the underlying disease.
When acids are placed into solution, there is dissociation of some of the component acid (HA) into its proton (H+) and free acid (A–). This is frequently written as an equation:
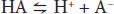
According to the laws of mass action, a relationship for the dissociation can be defined mathematically as:
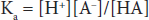
where Ka is a constant, and the brackets represent concentrations of the individual species. In layman’s terms, the product of the proton concentration ([H+]) times the free acid concentration ([A–]) divided by the bound acid concentration ([HA]) is a defined constant (K). This can be rearranged to read:
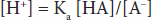
If the logarithm of each side is taken:
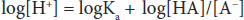
Both sides can be multiplied by –1 to yield:
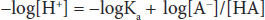
This can be written in a more conventional form known as the Henderson-Hasselbalch equation:
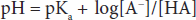
This relatively simple equation is quite powerful. One thing that can be discerned right away is that the buffering capacity of a particular weak acid is best when the pKa of that acid is equal to the pH of the solution, or when:
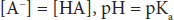
Similar equations can be set up for weak bases. An important buffer in the body is carbonic acid. Carbonic acid is a weak acid, and thus is only partly dissociated into H+ and HCO3–:
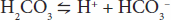
If H+ is added to a solution of carbonic acid, the equilibrium shifts to the left and most of the added H+ is removed from solution. If OH– is added, H+ and OH– combine, taking H+ out of solution. However, the decrease is countered by more dissociation of H2CO3, and the decline in H+ concentration is minimized. A unique feature of HCO3– is the linkage between its buffering ability and the ability for the lungs to remove CO2 from the body. Other important biologic buffers include phosphates and proteins.
Diffusion is the process by which a gas or a substance in a solution expands, because of the motion of its particles, to fill all the available volume. The particles (molecules or atoms) of a substance dissolved in a solvent are in continuous random movement. A given particle is equally likely to move into or out of an area in which it is present in high concentration. However, because there are more particles in the area of high concentration, the total number of particles moving to areas of lower concentration is greater; that is, there is a net flux of solute particles from areas of high concentration to areas of low concentration. The time required for equilibrium by diffusion is proportional to the square of the diffusion distance. The magnitude of the diffusing tendency from one region to another is directly proportional to the cross-sectional area across which diffusion is taking place and the concentration gradient, or chemical gradient, which is the difference in concentration of the diffusing substance divided by the thickness of the boundary (Fick’s law of diffusion). Thus,
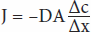
where J is the net rate of diffusion, D is the diffusion coefficient, A is the area, and Δc/Δx is the concentration gradient. The minus sign indicates the direction of diffusion. When considering movement of molecules from a higher to a lower concentration, Δc/Δx is negative, so multiplying by –DA gives a positive value. The permeabilities of the boundaries across which diffusion occurs in the body vary, but diffusion is still a major force affecting the distribution of water and solutes.
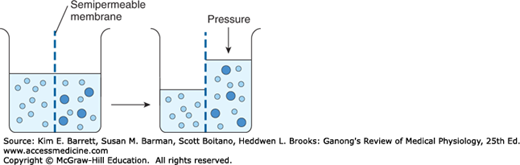
When a substance is dissolved in water, the concentration of water molecules in the solution is less than that in pure water, because the addition of solute to water results in a solution that occupies a greater volume than does the water alone. If the solution is placed on one side of a membrane that is permeable to water but not to the solute, and an equal volume of water is placed on the other, water molecules diffuse down their concentration (chemical) gradient into the solution (Figure 1–3). This process—the diffusion of solvent molecules into a region in which there is a higher concentration of a solute to which the membrane is impermeable—is called osmosis. It is an important factor in physiologic processes. The tendency for movement of solvent molecules to a region of greater solute concentration can be prevented by applying pressure to the more concentrated solution. The pressure necessary to prevent solvent migration is the osmotic pressure of the solution.
FIGURE 1–3
Diagrammatic representation of osmosis. Water molecules are represented by small open circles, and solute molecules by large solid circles. In the diagram on the left, water is placed on one side of a membrane permeable to water but not to solute, and an equal volume of a solution of the solute is placed on the other. Water molecules move down their concentration (chemical) gradient into the solution, and, as shown in the diagram on the right, the volume of the solution increases. As indicated by the arrow on the right, the osmotic pressure is the pressure that would have to be applied to prevent the movement of the water molecules.
Osmotic pressure—like vapor pressure lowering, freezing-point depression, and boiling-point elevation—depends on the number rather than the type of particles in a solution; that is, it is a fundamental colligative property of solutions. In an ideal solution, osmotic pressure (P) is related to temperature and volume in the same way as the pressure of a gas:
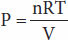
where n is the number of particles, R is the gas constant, T is the absolute temperature, and V is the volume. If T is held constant, it is clear that the osmotic pressure is proportional to the number of particles in solution per unit volume of solution. For this reason, the concentration of osmotically active particles is usually expressed in osmoles. One osmole (Osm) equals the gram-molecular weight of a substance divided by the number of freely moving particles that each molecule liberates in solution. For biologic solutions, the milliosmole (mOsm; 1/1000 of 1 Osm) is more commonly used.
If a solute is a nonionizing compound such as glucose, the osmotic pressure is a function of the number of glucose molecules present. If the solute ionizes and forms an ideal solution, each ion is an osmotically active particle. For example, NaCl would dissociate into Na+ and Cl– ions, so that each mole in solution would supply 2 Osm. One mole of Na2SO4 would dissociate into Na+, Na+, and SO42– supplying 3 Osm. However, the body fluids are not ideal solutions, and although the dissociation of strong electrolytes is complete, the number of particles free to exert an osmotic effect is reduced owing to interactions between the ions. Thus, it is actually the effective concentration (activity) in the body fluids rather than the number of equivalents of an electrolyte in solution that determines its osmotic capacity. This is why, for example, 1 mmol of NaCl per liter in the body fluids contributes somewhat less than 2 mOsm of osmotically active particles per liter. The more concentrated the solution, the greater the deviation from an ideal solution.
The osmolal concentration of a substance in a fluid is measured by the degree to which it depresses the freezing point, with 1 mol of an ideal solution depressing the freezing point by 1.86°C. The number of milliosmoles per liter in a solution equals the freezing point depression divided by 0.00186. The osmolarity is the number of osmoles per liter of solution (eg, plasma), whereas the osmolality is the number of osmoles per kilogram of solvent. Therefore, osmolarity is affected by the volume of the various solutes in the solution and the temperature, while the osmolality is not. Osmotically active substances in the body are dissolved in water, and the density of water is 1, so osmolal concentrations can be expressed as osmoles per liter (Osm/L) of water. In this book, osmolal (rather than osmolar) concentrations are considered, and osmolality is expressed in milliosmoles per liter (of water).
Note that although a homogeneous solution contains osmotically active particles and can be said to have an osmotic pressure, it can exert an osmotic pressure only when it is in contact with another solution across a membrane permeable to the solvent but not to the solute.
The freezing point of normal human plasma averages –0.54°C, which corresponds to an osmolal concentration in plasma of 290 mOsm/L. This is equivalent to an osmotic pressure against pure water of 7.3 atmospheres (atm). The osmolality might be expected to be higher than this, because the sum of all the cation and anion equivalents in plasma is over 300 mOsm/L. It is not this high because plasma is not an ideal solution and ionic interactions reduce the number of particles free to exert an osmotic effect. Except when there has been insufficient time after a sudden change in composition for equilibrium to occur, all fluid compartments of the body are in (or nearly in) osmotic equilibrium. The term tonicity is used to describe the osmolality of a solution relative to plasma. Solutions that have the same osmolality as plasma are said to be isotonic; those with greater osmolality are hypertonic; and those with lesser osmolality are hypotonic. All solutions that are initially isosmotic with plasma (ie, that have the same actual osmotic pressure or freezing-point depression as plasma) would remain isotonic if it were not for the fact that some solutes diffuse into cells and others are metabolized. Thus, a 0.9% saline solution remains isotonic because there is no net movement of the osmotically active particles in the solution into cells and the particles are not metabolized. On the other hand, a 5% glucose solution is isotonic when initially infused intravenously, but glucose is metabolized, so the net effect is that of infusing a hypotonic solution.
It is important to note the relative contributions of the various plasma components to the total osmolal concentration of plasma. All but about 20 of the 290 mOsm in each liter of normal plasma are contributed by Na+ and its accompanying anions, principally Cl– and HCO3–. Other cations and anions make a relatively small contribution. Although the concentration of the plasma proteins is large when expressed in grams per liter, they normally contribute less than 2 mOsm/L because of their very high molecular weights. The major nonelectrolytes of plasma are glucose and urea, which in the steady state are in equilibrium with cells. Their contributions to osmolality are normally about 5 mOsm/L each but can become quite large in hyperglycemia or uremia. The total plasma osmolality is important in assessing dehydration, overhydration, and other fluid and electrolyte abnormalities (Clinical Box 1–3).
Some weak acids and bases are quite soluble in cell membranes in the undissociated form, whereas they cannot cross membranes in the charged (ie, dissociated) form. Consequently, if molecules of the undissociated substance diffuse from one side of the membrane to the other and then dissociate, there is appreciable net movement of the undissociated substance from one side of the membrane to the other. This phenomenon is called nonionic diffusion.
CLINICAL BOX 1–3 Plasma Osmolality & Disease
Unlike plant cells, which have rigid walls, animal cell membranes are flexible. Therefore, animal cells swell when exposed to extracellular hypotonicity and shrink when exposed to extracellular hypertonicity. Cells contain ion channels and pumps that can be activated to offset moderate changes in osmolality; however, these can be overwhelmed under certain pathologies. Hyperosmolality can cause coma (hyperosmolar coma). Because of the predominant role of the major solutes and the deviation of plasma from an ideal solution, one can ordinarily approximate the plasma osmolality within a few mOsm/L by using the following formula, in which the constants convert the clinical units to millimoles of solute per liter:
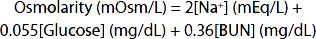
BUN is the blood urea nitrogen. The formula is also useful in calling attention to abnormally high concentrations of other solutes. An observed plasma osmolality (measured by freezing-point depression) that greatly exceeds the value predicted by this formula probably indicates the presence of a foreign substance such as ethanol, mannitol (sometimes injected to shrink swollen cells osmotically), or poisons such as ethylene glycol (component of antifreeze) or methanol (alternative automotive fuel).
When an ion on one side of a membrane cannot diffuse through the membrane, the distribution of other ions to which the membrane is permeable is affected in a predictable way. For example, the negative charge of a nondiffusible anion hinders diffusion of the diffusible cations and favors diffusion of the diffusible anions. Consider the following situation,
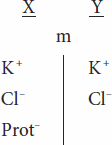
in which the membrane (m) between compartments X and Y is impermeable to charged proteins (Prot–) but freely permeable to K+ and Cl–. Assume that the concentrations of the anions and of the cations on the two sides are initially equal. Cl– diffuses down its concentration gradient from Y to X, and some K+ moves with the negatively charged Cl– because of its opposite charge. Therefore,
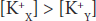
Furthermore,

that is, more osmotically active particles are on side X than on side Y.
Donnan and Gibbs showed that in the presence of a nondiffusible ion, the diffusible ions distribute themselves so that at equilibrium their concentration ratios are equal:
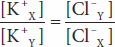
Cross-multiplying,
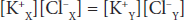
This is the Gibbs–Donnan equation. It holds for any pair of cations and anions of the same valence.
The Donnan effect on the distribution of ions has three effects in the body introduced here and discussed below. First, because of charged proteins (Prot–) in cells, there are more osmotically active particles in cells than in interstitial fluid, and because animal cells have flexible walls, osmosis would make them swell and eventually rupture if it were not for Na, K ATPase pumping ions back out of cells. Thus, normal cell volume and pressure depend on Na, K ATPase. Second, because at equilibrium the distribution of permeant ions across the membrane (m in the example used here) is asymmetric, an electrical difference exists across the membrane whose magnitude can be determined by the Nernst equation (see below). In the example used here, side X will be negative relative to side Y. The charges line up along the membrane, with the concentration gradient for Cl– exactly balanced by the oppositely directed electrical gradient, and the same holds true for K+. Third, because there are more proteins in plasma than in interstitial fluid, there is a Donnan effect on ion movement across the capillary wall.
The forces acting across the cell membrane on each ion can be analyzed mathematically. Chloride ions (Cl–) are present in higher concentration in the ECF than in the cell interior, and they tend to diffuse along this concentration gradient into the cell. The interior of the cell is negative relative to the exterior, and chloride ions are pushed out of the cell along this electrical gradient. An equilibrium is reached between Cl– influx and Cl– efflux. The membrane potential at which this equilibrium exists is the equilibrium potential. Its magnitude can be calculated from the Nernst equation, as follows:
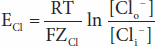
where
ECl = equilibrium potential for Cl–
R = gas constant
T = absolute temperature
F = the Faraday number (number of coulombs per mole of charge)
ZCl = valence of Cl– (–1)
[Clo–] = Cl– concentration outside the cell
[Cli–] = Cl– concentration inside the cell
Converting from the natural log to the base 10 log and replacing some of the constants with numeric values holding temperature at 37°C, the equation becomes:
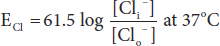
Note that in converting to the simplified expression the concentration ratio is reversed because the –1 valence of Cl– has been removed from the expression.
The equilibrium potential for Cl– (ECl) in the mammalian spinal neuron, calculated from the standard values listed in Table 1–1, is –70 mV, a value identical to the typical measured resting membrane potential of –70 mV. Therefore, no forces other than those represented by the chemical and electrical gradients need be invoked to explain the distribution of Cl– across the membrane.
A similar equilibrium potential can be calculated for K+ (EK; again, at 37°C):
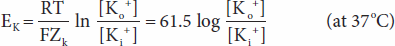
where
EK = equilibrium potential for K+
ZK = valence of K+ (+1)
[Ko+] = K+ concentration outside the cell
[Ki+] = K+ concentration inside the cell R, T, and F as above
In this case, the concentration gradient is outward and the electrical gradient inward. In mammalian spinal motor neurons EK is –90 mV (Table 1–1). Because the resting membrane potential is –70 mV, there is somewhat more K+ in the neurons that can be accounted for by the electrical and chemical gradients.
The situation for Na+ in the mammalian spinal motor neuron is quite different from that for K+ or Cl–. The direction of the chemical gradient for Na+ is inward, to the area where it is in lesser concentration, and the electrical gradient is in the same direction. ENa is +60 mV (Table 1–1). Because neither EK nor ENa is equal to the membrane potential, one would expect the cell to gradually gain Na+ and lose K+ if only passive electrical and chemical forces were acting across the membrane. However, the intracellular concentration of Na+ and K+ remain constant because selective permeability and because of the action of the Na, K ATPase that actively transports Na+ out of the cell and K+ into the cell (against their respective electrochemical gradients).
The distribution of ions across the cell membrane and the nature of this membrane provide the explanation for the membrane potential. The concentration gradient for K+ facilitates its movement out of the cell via K+ channels, but its electrical gradient is in the opposite (inward) direction. Consequently, an equilibrium is reached in which the tendency of K+ to move out of the cell is balanced by its tendency to move into the cell, and at that equilibrium there is a slight excess of cations on the outside and anions on the inside. This condition is maintained by Na, K ATPase, which uses the energy of ATP to pump K+ back into the cell and keeps the intracellular concentration of Na+ low. Because the Na, K ATPase moves three Na+ out of the cell for every two K+ moved in, it also contributes to the membrane potential, and thus is termed an electrogenic pump. It should be emphasized that the number of ions responsible for the membrane potential is a minute fraction of the total number present and that the total concentrations of positive and negative ions are equal everywhere except along the membrane.
ENERGY PRODUCTION
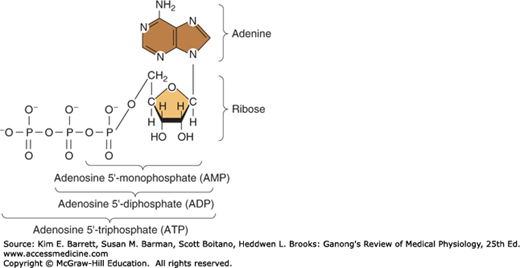
Energy used in cellular processes is primarily stored in bonds between phosphoric acid residues and certain organic compounds. Because the energy of bond formation in some of these phosphates is particularly high, relatively large amounts of energy (10–12 kcal/mol) are released when the bond is hydrolyzed. Compounds containing such bonds are called high-energy phosphate compounds. Not all organic phosphates are of the high-energy type. Many, like glucose 6-phosphate, are low-energy phosphates that on hydrolysis liberate 2–3 kcal/mol. Some of the intermediates formed in carbohydrate metabolism are high-energy phosphates, but the most important high-energy phosphate compound is adenosine triphosphate (ATP). This ubiquitous molecule (Figure 1–4) is the energy storehouse of the body. On hydrolysis to adenosine diphosphate (ADP), it liberates energy directly to such processes as muscle contraction, active transport, and the synthesis of many chemical compounds. Loss of another phosphate to form adenosine monophosphate (AMP) releases more energy.
FIGURE 1–4
Energy-rich adenosine derivatives. Adenosine triphosphate is broken down into its backbone purine base and sugar (at right) as well as its high energy phosphate derivatives (across bottom). (Reproduced with permission from Murray RK, et al: Harper’s Biochemistry, 28th ed. New York, NY: McGraw-Hill; 2009.)
Another group of high-energy compounds are the thioesters, the acyl derivatives of mercaptans. Coenzyme A (CoA)
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree