INTRODUCTION
Before the discovery of general anesthetics, pain and shock severely limited the possibilities for surgical intervention. Postoperative mortality dropped dramatically following the first public demonstration of diethyl ether at Massachusetts General Hospital in 1846. Since then, the administration of agents for the induction and maintenance of anesthesia has become a separate medical specialty. The modern anesthesiologist is responsible for all aspects of patient health during surgery. As part of this process, the anesthesiologist controls the depth of anesthesia and maintains homeostatic equilibrium with an arsenal of inhaled and intravenous anesthetics as well as many adjuvant drugs.
General anesthetics induce a generalized, reversible depression of the central nervous system (CNS). Under general anesthesia, there is a lack of perception of all sensations. The anesthetic state includes loss of consciousness, amnesia, and immobility (a lack of response to noxious stimuli) but not necessarily complete analgesia. Other desirable effects provided by anesthetics or adjuvants during surgery may include muscle relaxation, loss of autonomic reflexes, analgesia, and anxiolysis. All of these effects facilitate safe and painless completion of the procedure; some effects are more important in certain types of surgery than others. For example, abdominal surgery necessitates near-complete relaxation of the abdominal muscles, whereas neurosurgery often requires light anesthesia that may be lifted rapidly when the neurosurgeon needs to judge the patient’s ability to respond to commands.
This chapter provides a framework for understanding the pharmacodynamics and pharmacokinetics of general anesthetics in the context of physiologic and pathophysiologic variables. After discussing the pharmacology of specific agents and how a balanced anesthetic approach is achieved, the chapter considers what is currently known about the mechanism of action of general anesthetics.
Matthew is a 7-year-old, 20-kg boy who has been undergoing multidrug chemotherapy for aggressive osteosarcoma of his right femur. The time has now come for a surgical resection.
8:00 PM (night before the operation): Dr. Snow, the anesthesiologist, provides reassurance and revisits the importance of fasting after midnight to prevent aspiration of gastric contents while under general anesthesia.
6:30 AM: Matthew clings to his mother and appears anxious, cachectic, and in some pain. His vital signs are stable with an elevated pulse of 120 and a blood pressure of 110/75. An oral dose of midazolam (a benzodiazepine; see Chapter 13, Pharmacology of GABAergic and Glutamatergic Neurotransmission) is given to relieve anxiety and to allow Matthew to separate from his parents.
7:00 AM: Dr. Snow injects a small amount of lidocaine subcutaneously (a local anesthetic; see Chapter 12, Local Anesthetic Pharmacology) before inserting an intravenous catheter (which he carefully conceals from Matthew until the last possible moment). Through the catheter, Dr. Snow delivers an infusion of morphine sulfate (an opioid; see Chapter 18, Pharmacology of Analgesia) for analgesia.
7:30 AM: Dr. Snow rapidly induces anesthesia with an intravenous bolus of 60 mg (3 mg/kg) of thiopental (a barbiturate; see Chapter 13). Within 45 seconds, Matthew is in a deep anesthetic state. The doctor adds a dose of intravenous succinylcholine (a depolarizing muscle relaxant; see Chapter 10, Cholinergic Pharmacology) to facilitate endotracheal intubation, and Matthew is placed on artificial respiration.
7:32 AM: A mixture of inhaled general anesthetics consisting of 2% isoflurane, 50% nitrous oxide, and 48% oxygen is provided through the ventilator to maintain the anesthetic state.
7:50 AM: Matthew shows no response, either through movement or increased sympathetic tone (e.g., increased heart rate, increased blood pressure), to the first surgical incision.
8:20 AM: Dr. Snow notices with a start that Matthew’s pulse has fallen to 55 and his blood pressure to 85/45. Berating himself for forgetting to turn down the inspired partial pressure of the anesthetic as its mixed venous partial pressure increased, Dr. Snow reduces the inspired isoflurane level to 0.8% while keeping the nitrous oxide level at 50%. Within 15 minutes, Matthew’s pulse and blood pressure rebound.
12:35 PM: After a long surgery, Dr. Snow stops the isoflurane and nitrous oxide and turns on pure oxygen for a few minutes.
12:45 PM: In less than 10 minutes, Matthew is breathing spontaneously and is able to respond to questions, although he is still somewhat groggy. Matthew’s parents are relieved to find him awake and alert after more than 5 hours of anesthesia.
Questions
1. What determines the rate of induction and recovery from anesthesia, and how does this differ for children as compared to adults?
2. Why is it necessary to reduce the inspired partial pressure of isoflurane some minutes into the procedure (as Dr. Snow initially neglected to do)?
3. Why did Dr. Snow give pure oxygen for a few minutes following the cessation of anesthetic administration?
4. What are the advantages of using a mixture of two anesthetics (in this example, nitrous oxide and isoflurane) instead of just one or the other?
PHARMACODYNAMICS OF INHALED ANESTHETICS
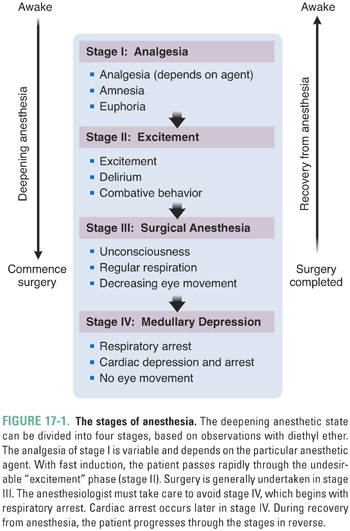
General anesthetics distribute well to all parts of the body, becoming most concentrated in the fatty tissues. The CNS is the primary site of action of anesthetics. Most likely, loss of consciousness and amnesia ensue from supraspinal action (i.e., action in the brainstem, midbrain, and cerebral cortex), while immobility in response to noxious stimuli is caused by depression of both supraspinal and spinal sensory and motor pathways. Different sites in the CNS are differentially affected by general anesthetics, giving rise to the classical stages observed with increasing anesthetic depth (Fig. 17-1).
The Minimum Alveolar Concentration (MAC)
To control the depth of anesthesia, the anesthesiologist must control rather precisely the level of anesthetic in the CNS. This level is denoted by the partial pressure of anesthetic in the CNS, also called the CNS partial pressure, PCNS. (See Box 17-1 for a discussion of partial pressures versus concentrations and Appendix A for a glossary of abbreviations and symbols.) The anesthesiologist maintains PCNS within the desired range by varying the inspired partial pressure, PI. Because the value of PCNS cannot be monitored directly, it is commonly inferred from the alveolar partial pressure, Palv. The alveolar partial pressure is a useful substitute for PCNS, because PCNS tracks Palv with only a small time lag (see below). Palv may be measured directly as the partial pressure of anesthetic in the end-tidal exhaled gas, when the dead space no longer contributes to the exhaled gas.
BOX 17-1 Partial Pressure Versus Concentration |
The partial pressure of Gas A in a mixture of gases is the portion of the total pressure that is supplied by Gas A. For ideal gases, the partial pressure of Gas A is obtained by multiplying the total pressure by the mole fraction of A in the mixture (i.e., the fraction of molecules in the mixture represented by Gas A). The concentration of Gas A in the mixture ([A]mixture) is the number of moles of Gas A (nA) divided by the volume (V); [A]mixture can also be obtained from the ideal gas equation by dividing the partial pressure of Gas A (PA) by the temperature (T) and the universal gas constant (R): [A]mixture = nA / V = PA / RT Inhaled anesthetics dissolve in the tissues of the body, such as the blood and the brain. The partial pressure of a gas dissolved in a liquid is equal to the partial pressure of free gas in equilibrium with that liquid. For gases, partial pressures are convenient because the partial pressures in all compartments are equal at equilibrium. This is true, independent of whether the compartments contain gas that is in the gaseous (alveoli) or the dissolved (tissues) form. In contrast, the concentrations within different compartments are not equal at equilibrium. To convert the partial pressure of a dissolved gas to its concentration within the solvent, the partial pressure is multiplied by a measure of solubility known as the solvent/gas partition coefficient. |
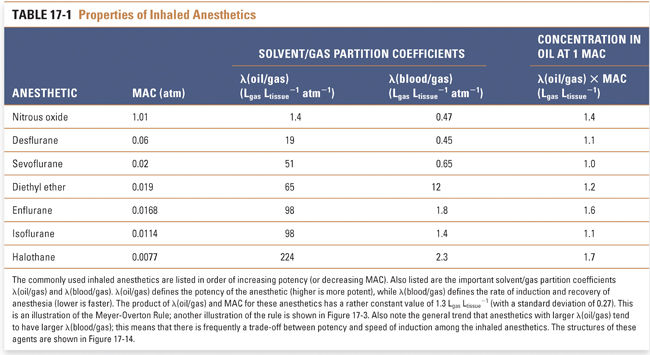
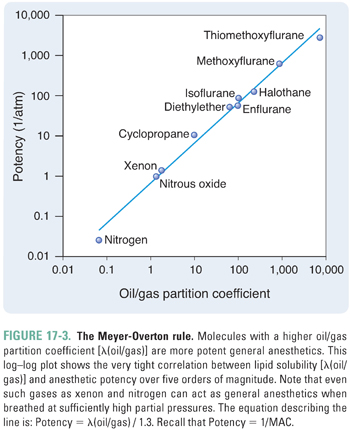
The alveolar partial pressure that results in the lightest possible anesthesia is termed the minimum alveolar concentration (MAC). Specifically, MAC is the alveolar partial pressure that abolishes a movement response to a surgical incision in 50% of patients. The potency of an anesthetic is related inversely to its MAC. If the MAC is small, then the potency is high, and a relatively low partial pressure will be sufficient to cause anesthesia. For example, isoflurane—which has a MAC of 0.0114 atm—is much more potent than nitrous oxide—which has a MAC of 1.01 atm (Table 17-1).
Therapeutic and Analgesic Indices
Loss of response to extremely noxious stimuli, such as endotracheal intubation, requires a higher partial pressure of anesthetic than is required for loss of response to a surgical incision (Fig. 17-2). Still higher partial pressures of anesthetic cause medullary depression. In general, however, anesthetics have steep dose–response curves and low therapeutic indices, defined as the ratio of LP50 (the partial pressure that is lethal in 50% of subjects) to MAC (which is analogous to ED50; see Chapter 2, Pharmacodynamics). Furthermore, the variability among patients in their response to a given dose of anesthetic is small. Therefore, for all patients, the levels of anesthetic that cause respiratory and cardiac arrest are not much higher than the levels that cause general anesthesia. It should also be noted that no pharmacologic antagonists of general anesthetics exist to counteract inadvertently high levels of anesthetic. Although these disadvantages are partially offset by the ability to control PCNS through control of PI (i.e., the anesthetic can be breathed out), the combination of low therapeutic index and lack of antagonist means that anesthetics are dangerous drugs that demand specialty training for their proper and safe administration.
Pain relief (analgesia) may or may not occur at a partial pressure lower than that required for surgical anesthesia. The partial pressure at which 50% of persons lose nociception is the AP50 (partial pressure that results in analgesia in 50% of patients), and the analgesic index is the ratio of MAC to AP50. A high analgesic index implies that analgesia is induced at a partial pressure of anesthetic significantly lower than that required for surgical anesthesia. For example, nitrous oxide has a high analgesic index and is a good analgesic, whereas halothane has a low analgesic index and is a poor analgesic.
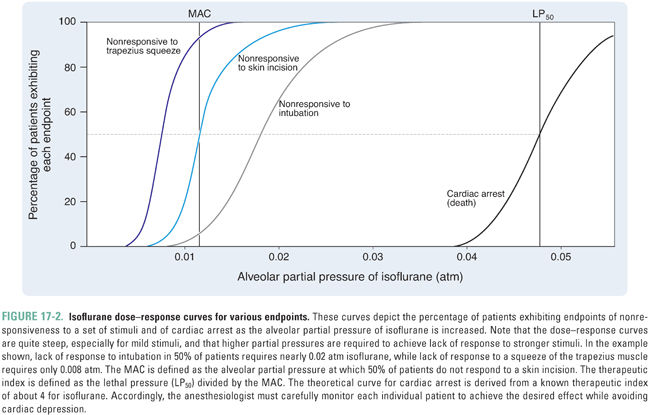
The potency of an anesthetic can be predicted from its physicochemical characteristics. The most reliable predictor has been the anesthetic’s solubility in olive oil (or in another lipophilic solvent, such as octanol), as denoted by the oil/gas partition coefficient, λ(oil/gas) (Box 17-2). Specifically, the potency of an anesthetic increases as its solubility in oil increases. That is, as λ(oil/gas) increases, MAC decreases.
BOX 17-2 Partition Coefficients |
The solvent/gas partition coefficient, λ(solvent/gas), defines the solubility of a gas in a solvent or, in other words, the extent to which the gas “partitions” between its gaseous state and the solution. More specifically, λ(solvent/gas) is the ratio of the amount of gas dissolved in a given volume of solvent to the amount of free gas that would occupy the same volume of space, all at standard temperature (25°C) and pressure (1.0 atm) (STP). The solvent could be olive oil, blood, or brain tissue, for example. Dissolved amounts of gas are typically given not in terms of moles but in terms of the volume that the gas would occupy at STP in a gaseous state. Recall that, to convert from moles to liters at STP, one multiplies by the volume of one mole of gas at 25°C and 1.0 atm (i.e., by 24.5 L/mol). Thus, λ(solvent/gas) is the number of liters of gas that will dissolve in one liter of solvent per atmosphere of partial pressure. [Note that the units of λ(solvent/gas) are Lgas Lsolvent−1 atm−1, or simply atm−1.] For a particular solvent, a gas with a larger λ(solvent/gas) is more soluble in that solvent. For example, diethyl ether has a λ(blood/gas) of about 12 Ldiethyl ether Lblood−1 atm−1, so diethyl ether is relatively soluble in blood. In contrast, nitrous oxide has a λ(blood/gas) of about 0.47 Lnitrous oxide Lblood−1 atm−1, so nitrous oxide is relatively insoluble in blood (see Table 17-1 and Fig. 17-8 for examples). Likewise, a gas may have different solubilities in different solvents. Solvents or tissues in which a gas has a high partition coefficient (high solubility) will dissolve large amounts of the gas at a given partial pressure, resulting in a high concentration of the gas in that solvent or tissue. Thus, large amounts of gas must be transferred to change the partial pressure by an appreciable amount. In contrast, solvents or tissues in which a gas has a low partition coefficient (low solubility) will dissolve only small amounts of the gas at a given partial pressure. In this case, transferring a small amount of the gas will significantly change the partial pressure (Fig. 17-8). For any given partial pressure, Henry’s law for dilute solutions allows the concentration of Gas A in a solvent ([A]solution) to be calculated from λ(solvent/gas). The partial pressure is multiplied by the partition coefficient to calculate the concentration in terms of Lgas per Lsolvent. The result is divided by the volume of one mole of gas at 25°C at 1.0 atm (24.5 L/mol) to yield the molar concentration. [A]solution = Psolvent × λ(solvent/gas) {in terms of Lgas/Lsolvent} = Psolvent × λ(solvent/gas)/(24.5 L/mol) {in terms of molgas/Lsolvent} For example, because the λ(blood/gas) of nitrous oxide is 0.47 Lnitrous oxide Lblood−1 atm−1, if the partial pressure of nitrous oxide in the blood is 0.50 atm, then the concentration is 0.50 atm × 0.47 Lnitrous oxide Lblood−1 atm−1 = 0.24 Lnitrous oxide Lblood−1 or 9.6 mM (after dividing by 24.5 L/mol). Also note that doubling the partial pressure will double the concentration. A partition coefficient can also be defined for the partitioning of a gas between two solvents. For example, the tissue/blood partition coefficient, λ(tissue/blood), is the ratio of the molar concentration of gas in the tissue ([A]tissue) to the molar concentration of gas in the blood ([A]blood) at equilibrium (note that this coefficient is unitless). From the previous equation defining concentration and the fact that partial pressures are equal at equilibrium, it follows that λ(tissue/blood) = [A]tissue/[A]blood = λ(tissue/gas)/λ(blood/gas) |
The relationship between MAC and λ(oil/gas) is such that MAC multiplied by λ(oil/gas) is nearly constant, independent of the identity of the anesthetic. Because multiplication of the partition coefficient by the partial pressure yields the concentration of anesthetic (Box 17-2), this is equivalent to saying that, at 1 MAC, the concentration of anesthetic in a lipophilic solvent (such as olive oil) is nearly constant for all anesthetics. Thus, the MAC, which varies with the identity of the anesthetic, is actually the partial pressure required to generate a particular concentration of anesthetic in a lipophilic medium, such as the lipid bilayers in the CNS. This correlation, known as the Meyer-Overton rule, holds over at least five orders of magnitude of anesthetic potency (Fig. 17-3). The constant that represents the concentration of anesthetic at 1 MAC is 1.3 liters of gas per liter of oil (Lgas / Loil), or 0.05 M after dividing by the volume of one mole (see Box 17-2). Thus, if one knows the oil/gas partition coefficient of an anesthetic, one can estimate its MAC from the following equation (see also Table 17-1):
PHARMACOKINETICS OF INHALED ANESTHETICS
A cardiopulmonary model of the uptake of anesthetic from the alveoli into the circulation and the distribution of anesthetic from the circulation to the tissues allows determination of the rate at which the partial pressure of anesthetic rises within the CNS. The anesthesiologist must navigate the small space between allowing a patient to awaken and causing medullary depression by predicting the effects of various physiologic responses and disease states on the depth of anesthesia. For example, an understanding of the distribution characteristics of anesthetics enabled Dr. Snow to respond appropriately to Matthew’s hypotension by lowering the PI of isoflurane without overcorrecting and causing him to awaken.
The anesthesiologist must also be aware of the differences in the pharmacokinetics of the various anesthetics. The pharmacokinetic characteristics of an ideal general anesthetic would be such that the anesthetic provides a rapid and pleasant induction of surgical anesthesia, followed by a smooth and rapid recovery to a fully functional and conscious state. The pharmacokinetics of individual agents are discussed below; this section deals with general principles of the uptake model, which uses basic respiratory and cardiovascular physiology to predict the pharmacokinetics of the inhaled anesthetics. As discussed below, the uptake model depends on calculations of the time required for the equilibration of anesthetic partial pressures in the tissues with the inspired anesthetic partial pressure.
Concepts from Respiratory Physiology
During general anesthesia, the patient breathes, either spontaneously or via a ventilator, an anesthetic or mixture of anesthetics together with oxygen and/or normal air. Once the anesthetic gas reaches the alveoli, it must diffuse across the respiratory epithelium into the alveolar capillary bed. According to Fick’s law, the rate of diffusion of gas through a sheet of tissue down its partial pressure gradient is proportional to the tissue area and the partial pressure difference between the two sides and is inversely proportional to the thickness of the sheet:
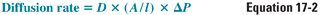
where D = diffusion constant; A = surface area; l = thickness; and ΔP = partial pressure difference.
One principle evident from Fick’s law is that the equalization of the partial pressure of the gas, not its concentration, defines the approach to equilibrium across a boundary sheet. Thus, at equilibrium (i.e., when the net diffusion rate is zero), the partial pressure in the two compartments is the same, even though the concentration in the two compartments may be different.
With its enormous alveolar surface area (~75 m2, or nearly half a tennis court) and thin epithelium (~0.3 μm, which is less than 1/20th the diameter of a red blood cell), the lung optimizes the rate of gas diffusion. Accordingly, the alveolar partial pressure Palv and the systemic arterial partial pressure Part are nearly the same at all times. (In normal individuals, small amounts of physiologic shunting keep Part slightly lower than Palv.) By using the lungs as an uptake system for inhaled anesthetics, anesthesiologists take advantage of the body’s system for absorbing oxygen.
Similarly, the capillary beds in tissues have evolved to deliver oxygen rapidly to all cells in the body. The distances between arterioles are small, and diffusion pathways are on the order of one cell diameter. Consequently, the arterial partial pressure of a general anesthetic can equilibrate completely with tissues in the time required for blood to traverse the capillary bed. Likewise, the partial pressure in the postcapillary venules Pvenule equals the partial pressure in the tissue Ptissue.
Another way of stating the above conclusion is that the transfer of anesthetic in both the lungs and the tissues is limited by perfusion rather than diffusion. Because perfusion is rate-limiting, increasing the rate of diffusion (e.g., by using a lower molecular weight anesthetic) will not, by itself, increase the rate of induction of anesthesia.
If an anesthetic is inspired for a sufficiently long period of time, all compartments in the body will equilibrate to the same partial pressure (equal to PI). This global equilibration may be divided into a series of partial pressure equilibrations between each successive compartment and its incoming flow of anesthetic. In the case of the tissues, the incoming flow is the arterial blood flow, with partial pressure approximately equal to Palv. In the case of the alveoli, the incoming flow is the alveolar ventilation with partial pressure PI.
The time constant τ describes the rate of approach of a compartment’s partial pressure to that of its incoming flow. Specifically, τ is the time required for equilibration to be 63% complete. This time constant is convenient because it can be calculated by dividing the compartment’s volume capacity (relative to the delivering medium; see below) by the flow rate. In other words, once a volume of flow equal to the capacity of a compartment has gone through that compartment, the partial pressure of anesthetic in the compartment (i.e., in the tissues or alveoli) will be 63% of the partial pressure in the incoming flow (i.e., in the arterial blood flow or alveolar ventilation, respectively). Equilibration is 95% complete after three time constants.
where t = elapsed time.
These equations describe what should make intuitive sense: equilibration of the partial pressure of the compartment with the incoming flow takes place more quickly (i.e., the time constant is smaller) when the inflow is larger or the compartment capacity is smaller.
For simplicity, the model of anesthetic uptake and distribution organizes the tissues of the body into groups based on similar characteristics. Each group can be modeled as a container with a particular capacity for anesthetic and a particular level of blood flow delivering anesthetic. An adequate approximation groups the tissues into three main compartments that are perfused in parallel (Fig. 17-4). The vessel-rich group (VRG), which consists of the CNS and visceral organs, has a low capacity and high flow. The muscle group (MG), which consists of muscle and skin, has a high capacity and moderate flow. The fat group (FG) has a very high capacity and low flow. (A fourth group, the vessel-poor group [VPG], which consists of bone, cartilage, and ligaments, has a negligible capacity and flow, and its omission does not significantly affect the model.)
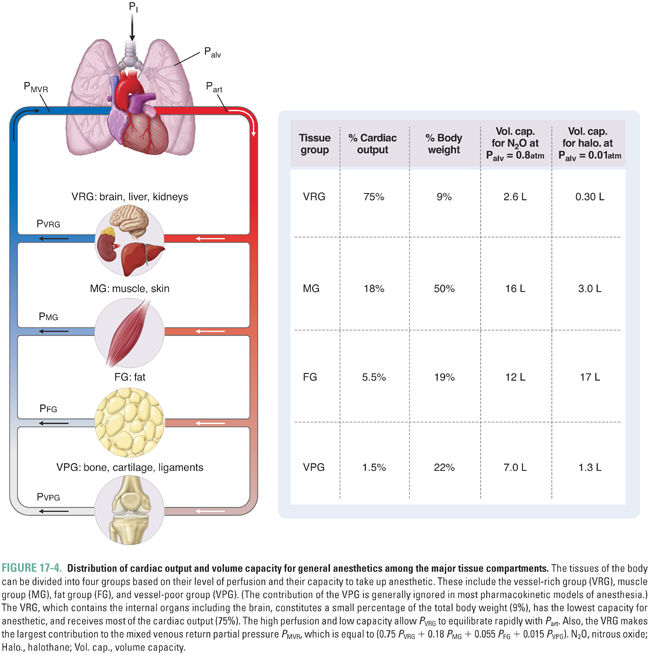
The rate of increase of the partial pressure in the VRG (PVRG) is of the greatest interest because the VRG includes the CNS. The overall equilibration of PVRG with the inspired partial pressure occurs in two steps, either of which may be rate-limiting. First, the alveolar and inspired partial pressures equilibrate (Palv approaches PI, or Palv → PI). Second, PVRG (and specifically PCNS) equilibrates with the arterial partial pressure (which is essentially equal to the alveolar partial pressure) (PVRG → Part). The discussion will now consider the time constant for each of these two steps and define conditions under which one or the other is rate-limiting.
Equilibration of Alveolar with Inspired Partial Pressure
The equilibration of Palv with PI is conceptually the first step of the equilibration of PVRG with PI. During induction of anesthesia, PVRG can never be higher than Palv; if Palv rises slowly, then PVRG must also rise slowly.
To calculate the time constant for the approach of Palv to PI, τ{Palv→PI}, the flow rate and volume capacity must be defined. The delivering medium is free gas arriving through the airways, and the compartment is the lung and alveoli. The volume capacity is simply the volume of gas that remains in the lungs after normal exhalation, or the functional residual capacity (FRC, typically ~3 L for an average adult). Assume initially that the only component of the flow rate is the rate of alveolar ventilation, which delivers the anesthetic (Valv = {Tidal Volume − Dead Space} × Respiratory Rate; for an average adult, Valv = {0.5 L − 0.125 L} × 16 min−1 ≈ 6 L/min). Then, because
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
