TERMS
•Arabic numbers
•Common fraction
•Decimal fraction
•Denominator
•Improper fraction
•Number
•Numeral
•Numerator
•Percent
•Proportion
•Ratio
•Reciprocal
•Roman numerals
•Significant figure
OBJECTIVES
Upon completion of this chapter, the technician student will be able to:
•Convert Roman numerals to Arabic numbers and convert Arabic numbers to Roman numerals.
•Reduce fractions to their lowest terms.
•Convert fractions into whole numbers and mixed numbers, and convert whole numbers and mixed numbers into fractions.
•Correctly add, subtract, multiply, and divide fractions, mixed numbers, and improper fractions.
•Correctly add, subtract, multiply, and divide decimal fractions.
•Correctly round decimals to a given place.
•Correctly convert fractions to decimals and decimals to fractions.
•Correctly change decimals and fractions to percents.
•Demonstrate an understanding of significant figures.
•Define ratio and proportion and calculate problems for a missing term using ratio and proportion.
This chapter focuses on a basic review of numbers, fractions, decimals, and their mathematical operations, as well as calculating basic ratio and proportion problems. The student will also be introduced briefly to dimensional analysis.
Numbers and Numerals
A number indicates the total quantity of units. A numeral is a word, sign, or group of words or signs expressing a number. For example 3, 6, and 48 are Arabic numerals expressing numbers that are, respectively, 3 times, 6 times, and 48 times the unit 1.
number A total quantity or amount of units.
numeral A word, symbol, or group of words or symbols that expresses a number.
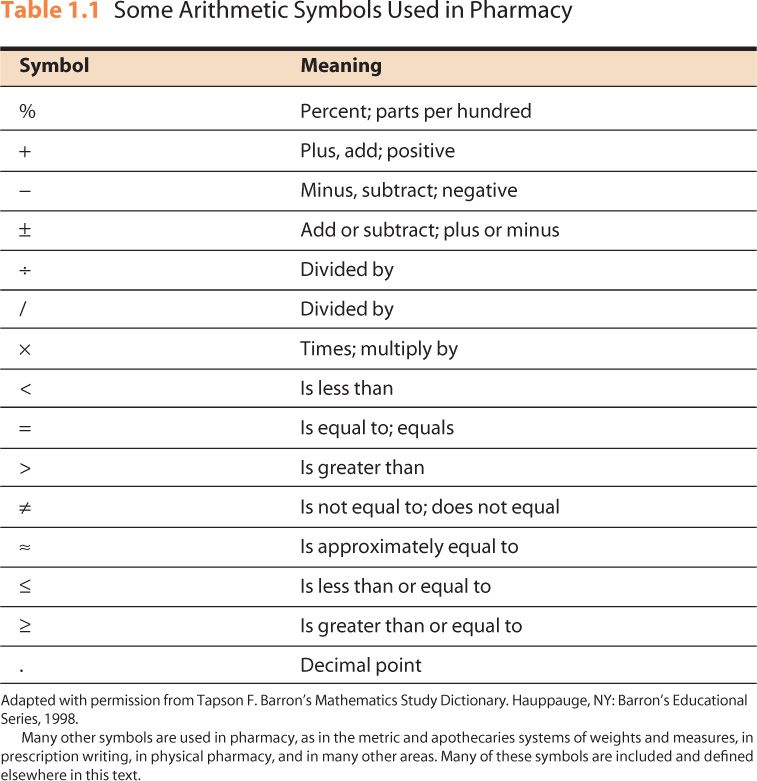
Many symbols in mathematics and science are used to provide instructions for a specific calculation or that indicate relative value. Some of the common symbols of arithmetic are presented in Table 1.1.
Kinds of Numbers
In arithmetic, the science of calculating with positive real numbers, the number is usually (a) a natural or whole number (integer), such as 549; (b) a fraction, or subdivision, of a whole number, such as 
; or (c) a mixed number, consisting of a whole number plus a fraction, or part, such as 
.
A number such as 4, 8, or 12, taken by itself without a label to indicate distinction, is called an abstract or pure number. It merely designates how many times the unit 1 is represented; it does not imply anything else about what is being counted or measured. An abstract number may be added to, subtracted from, multiplied by, or divided by any other abstract number. The result of any of these operations always results in an abstract number designating a new total of units.
A number that designates a quantity of objects or units of measure, such as 4 g, 8 mL, or 12 oz, is called a concrete or denominate number. It designates the total quantity of whatever is being measured. A denominate number has a label and indicates precisely what is to be counted or measured. A denominate number may be added to or subtracted from any other number of the same denomination, but a denominate number may be multiplied or divided only by a pure number. The result of these operations is always the same denomination.
Examples:
4 apples + 6 apples = 10 apples
10 g − 5 g = 5 g
4 apples × 2 = 8 apples
12 oz ÷ 3 = 4 oz
Differing Denominations Rule
Numbers of different denominations cannot be added or subtracted from one another. For example, it is not possible to add four apples and three oranges; a common denominator is necessary. Four pieces of fruit can be added to three pieces of fruit to get seven pieces of fruit. A denominate number can be multiplied or divided by a different denomination, in fact the multiplier or divisor is an abstract number. For example, if 1 oz costs $0.05, to find the cost of 12 oz, one multiplies $0.05 not by 12 oz but by the abstract number 12 to get the cost of $0.60 for 12 oz.
Arabic Numbers
The Arabic system of notation is the one we are most familiar with. It uses the Arabic numbers 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. These numbers can be written as fractions or decimals.
Arabic numbers The standard set of symbols, 1, 2, 3, and so on, to designate units. Arabic numbers are used in fractions and decimals.
Roman Numerals
The Roman numeral system of notation dates to the ancient days of Rome and uses letters to designate amounts. Roman numerals merely record quantities; they are of no use in computations. Roman numerals were used exclusively in the apothecaries’ system of measure. We will see this number system used in prescription and medication orders to indicate doses.
Roman numerals A numbering system using the letters I, V, X, L, C, D, and M to designate units. This system dates to ancient Rome and is used in the apothecary system of measure.
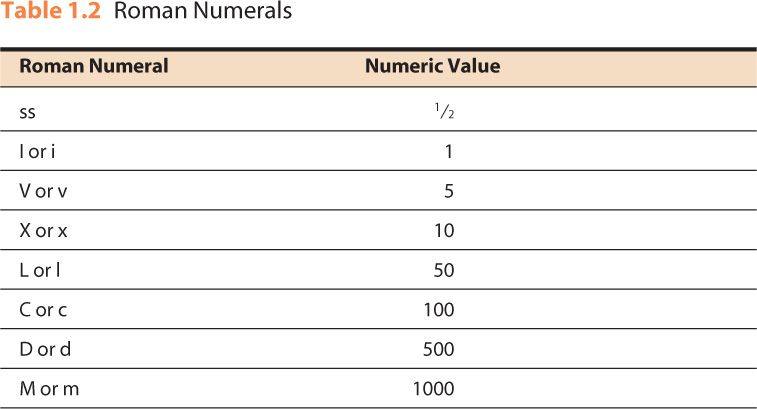
To express quantities in the Roman system, eight letters of fixed values are used, as shown in Table 1.2.
When Roman numerals are written in lowercase letters i, vi, xii, they may be topped by a horizontal line to help avoid errors. In the case of i the dot is above the line.
Rules to Apply to Roman Numerals
•When a Roman numeral of equal or lesser value is placed after one of equal or greater value, the value of the numerals is added. A numeral is not repeated more than three times.
•When a Roman numeral of lesser value is placed before a numeral of greater value, the value of the first numeral is subtracted from the numeral of greater value.
Review Set 1.1: Arabic and Roman Numerals
Write the Roman numerals for the following:
1.4
2.8
3.½
4.18
5.64
6.37
7.99
8.48
9.20
10.45
Write the Arabic numbers for the following:
11.IV
12.XXIV
13.xix
14.XC
15.xlv
16.xii
17.MDCCCXIV
18.ii
19.CCLVII
20.CCIV
Interpret the quantity in each of the phrases taken from prescriptions:
21.Capsules no. xlv
22.Drops ii
23.Tablets no. XLVIII
24.Ounces no. lxiv
25.Lozenges no. xvi
26.Transdermal patches no. LXXXIV
27.Tablets no. xxiv
28.Ounces no. viii
29.Capsules no. C
30.Troches no. xxxv
Common Fractions, Decimal Fractions, and Percents
The arithmetic of pharmacy requires expertise in the handling of common fractions and decimal fractions. Even if the student technician already has a good working knowledge of their use, the following brief review of certain principles and rules should be helpful, and the practice problems should provide a means of gaining accuracy and speed in their manipulations.
Fractions
Fractions are an expression of parts of a whole number. A fraction contains two parts: a numerator, the top number, expresses the number of parts in question; the denominator, the bottom number, expresses the total parts of the whole number (Fig. 1.1).
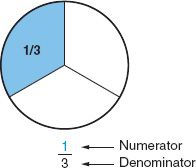
Figure 1.1Numerator and denominator.
numerator The top number of a fraction, which indicates the number of parts in question. For example, in 
, the whole is three parts; the number of parts in question is 1.
denominator The bottom number in a fraction; it indicates the number of parts in the whole. For example, in 
, the number of parts in the whole is 3.
In a common fraction, also called a proper fraction, the numerator is less than the denominator. The value of a common or proper fraction is less than one. (The value of a fraction is the numerator divided by the denominator.) Examples of common fractions include 
, 
, ½, and 
.
common fraction A part of a whole number, sometimes termed a proper fraction (e.g., ½); the numerator is less than the denominator. The value of a common or proper fraction is less than 1.
In an improper fraction the numerator is larger than the denominator, and the value is greater than 1. Examples include 
and 
improper fraction A fraction with the numerator (top number) larger than the denominator (bottom number). The value of an improper fraction is greater than 1.
A mixed number is a whole number and a fraction, such as 1½ or 3
. Mixed numbers can easily be converted into improper fractions by following the principles governing arithmetical operations for fractions.
Fundamental Rules of Fractions
•Multiplying or dividing the numerator and denominator of a fraction by the same number does not change the value of the fraction.
•To change a fraction to its lowest terms, divide its numerator and its denominator by the largest whole number that will go into both evenly.
•The lowest common denominator is the smallest whole number that can be divided evenly by all of the denominators in a problem.
Example of multiplying or dividing the numerator and denominator of a fraction by the same number:
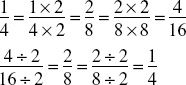
Therefore, the lowest term for 
is ¼. Figure 1.2 illustrates this point.
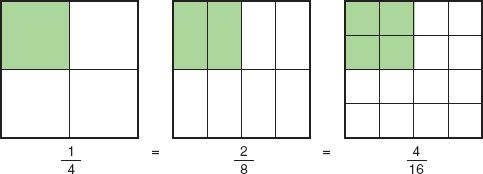
Figure 1.2Fractions.
Example of changing a fraction to its lowest terms:
The first fundamental rule of fractions allows us to reduce fractions to the lowest common denominator, which is the smallest number divisible by all of the other given denominators.
Reduce 
to its lowest terms.
The largest common divisor is 36.
Example of finding the lowest common denominator:
Reduce the fractions ¾, 
, and 
to a common denominator.
By testing successive multiples of 5, we discover that 60 is the smallest number divisible by 4, 5, and 3; 4 is contained 15 times in 60; 5, 12 times; and 3, 20 times.
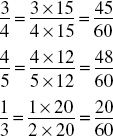
Rules Governing Arithmetical Operations of Fractions
•Reduce every mixed and improper fraction.
•Express whole numbers as a fraction having 1 for its denominator.
Rules for Adding Fractions
Step 1.Convert fractions to lowest common denominator if necessary.
Step 2.Add numerators; place sum over denominator.
Step 3.Reduce to lowest terms.
The first rule for adding fractions states that it is necessary to convert fractions to the lowest common denominator. This is accomplished using the third fundamental rule of fractions, remembering that the lowest common denominator is the smallest number into which all of the denominators will divide evenly.
Examples:
answer
Reduce by dividing both the numerator and denominator by 2:
answer
¼ + 
=
Find the lowest common denominator.
The lowest common denominator is 12.
answer
Convert the mixed number into an improper fraction:
Reduce:
answer
In preparing batches of a formula, a pharmacist used ¼ oz, 
oz, 
oz, and 
oz of a chemical. Calculate the total quantity used.
The lowest common denominator is 24.
and 
Reduce:
oz, answer
Rules for Subtracting Fractions
Step 1.Convert fractions to lowest common denominator if necessary.
Step 2.Subtract the numerators and place the amount over the denominator.
Step 3.Reduce to lowest terms.
Examples:
Lowest common denominator is 6.
Reduce:
answer
− 2
=Convert mixed numbers into improper fractions:
Reduce:
answer
A hospitalized patient received 
L of a prescribed intravenous infusion. If he had not received the final 
L, what fraction of a liter would he have received?
The lowest common denominator is 24.
L, answer
Rules for Multiplying Fractions
Step 1.Convert mixed numbers into improper fractions.
Step 2.Multiply the numerators to get a new numerator.
Step 3.Multiply the denominators to get a new denominator.
Step 4.Reduce to lowest terms.
Examples:
Reduce:
, answer
¼ × ½ = 
, answer
2
× 1½ =
Convert mixed numbers to improper fractions:
Reduce:
answer
If the adult dose of a medication is 2 teaspoonfuls and the child dose is ¼ the adult dose, calculate the dose for a child.
Reduce:
½ teaspoonful, answer
Rules for Dividing Fractions
Step 1.Convert mixed numbers into improper fractions.
Step 2.Find the reciprocal of the divisor (the second fraction) (invert the second fraction) and multiply.
Step 3.Reduce to lowest terms.
reciprocal 1 divided by the number in question.
Examples:
Reduce:
1½, answer
Reduce:
answer
If ½ oz is divided into 4 equal parts, how much will each part contain?
½ oz ÷ 
= ½ × ¼ = 
oz, answer
A manufacturer wishes to prepare samples of an ointment in sealed foil envelopes, each containing 
oz of ointment. How many samples may be prepared from 1 lb (16 oz) of ointment?
samples, answer
If a child’s dose of a cough syrup is ¾ teaspoonful and that is ¼ of the adult dose, what is the adult dose?
tsp, answer
Indicate which fraction is the smallest:
1.
2.
3.
Indicate which fraction is the largest:
4.
5.
6.
Reduce the following to the lowest terms:
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
Add the following:
17. 
+ ½
18.2½ + 4¼
19.
20.
21.
Subtract the following:
22.¾ − ½ =
23.2
− 1
24.
25.
26.
27.
Find the product of the following:
28.½ × 
29.
× ¾
30.
31.
32.
33.
34.
35.6 × 
36.3
× 4½
37.
× 
38.
39.¼ × ½ × 
40.
41.2½ × 12 × 
42.
What is the reciprocal of each of the following?
43.
44.3
45.
46.
47.1
48.
Find the quotient of each of the following:
49.2 ÷ ½
50.
÷ ¼
51.
52.25 ÷ ½
53.
54.2 ÷ 
55.
56.3
÷ 4
57.50 ÷ ½
58.
59.
60.6¼ ÷ ½
61.
62.A cookie mix makes 36 cookies. The day care provider gives each child 3 cookies. What fractional part of the batch did each child receive?
63.A bottle of Tylenol® children’s liquid contains 24 doses, each measuring 5 mL. If one child receives 4 doses, what fractional part of the bottle does the child receive?
