8
Enzymes: Kinetics

Peter J. Kennelly, PhD & Victor W. Rodwell, PhD

BIOMEDICAL IMPORTANCE

Enzyme kinetics is the field of biochemistry concerned with the quantitative measurement of the rates of enzyme-catalyzed reactions and the systematic study of factors that affect these rates. Kinetic analysis can reveal the number and order of the individual steps by which enzymes transform substrates into products. Together with site-directed mutagenesis and other techniques that probe the protein structure, kinetic analyses can reveal details of the catalytic mechanism of a given enzyme.

A complete, balanced set of enzyme activities is of fundamental importance for maintaining homeostasis. An understanding of enzyme kinetics thus is important to understanding how physiologic stresses such as anoxia, metabolic acidosis or alkalosis, toxins, and pharmacologic agents affect that balance. The involvement of enzymes in virtually all physiologic processes makes them the targets of choice for drugs that cure or ameliorate human disease. Applied enzyme kinetics represents the principal tool by which scientists identify and characterize therapeutic agents that selectively inhibit the rates of specific enzyme-catalyzed processes. Enzyme kinetics thus plays a central and critical role in drug discovery and comparative pharmacodynamics, as well as in elucidating the mode of action of drugs.

CHEMICAL REACTIONS ARE DESCRIBED USING BALANCED EQUATIONS

A balanced chemical equation lists the initial chemical species (substrates) present and the new chemical species (products) formed for a particular chemical reaction, all in their correct proportions or stoichiometry. For example, balanced equation (1) describes the reaction of one molecule each of substrates A and B to form one molecule each of products P and Q:

The double arrows indicate reversibility, an intrinsic property of all chemical reactions. Thus, for reaction (1), if A and B can form P and Q, then P and Q can also form A and B. Designation of a particular reactant as a “substrate” or “product” is therefore somewhat arbitrary since the products for a reaction written in one direction are the substrates for the reverse reaction. The term “products” is, however, often used to designate the reactants whose formation is thermodynamically favored. Reactions for which thermodynamic factors strongly favor formation of the products to which the arrow points often are represented with a single arrow as if they were “irreversible”:

Unidirectional arrows are also used to describe reactions in living cells where the products of reaction (2) are immediately consumed by a subsequent enzyme-catalyzed reaction. The rapid removal of product P or Q therefore effectively precludes occurrence of the reverse reaction, rendering equation (2) functionally irreversible under physiologic conditions.

CHANGES IN FREE ENERGY DETERMINE THE DIRECTION & EQUILIBRIUM STATE OF CHEMICAL REACTIONS

The Gibbs free energy change ΔG (also called either free energy or Gibbs energy) describes both the direction in which a chemical reaction will tend to proceed and the concentrations of reactants and products that will be present at equilibrium. ΔG for a chemical reaction equals the sum of the free energies of formation of the reaction products ΔG_p minus the sum of the free energies of formation of the substrates ΔG_s. ΔG⁰ denotes the change in free energy that accompanies transition from the standard state, one-molar concentrations of substrates and products, to equilibrium. A more useful biochemical term is ΔG⁰’, which defines ΔG⁰ at a standard state of 10^–7 M protons, pH 7.0 (Chapter 11). If the free energy of formation of the products is lower than that of the substrates, the signs of ΔG⁰ and ΔG^0’ will be negative, indicating that the reaction as written is favored in the direction left to right. Such reactions are referred to as spontaneous. The sign and the magnitude of the free energy change determine how far the reaction will proceed. Equation (3) illustrates the relationship between the equilibrium constant K_eq and ΔG⁰:

where R is the gas constant (1.98 cal/mol°K or 8.31 J/mol°K) and T is the absolute temperature in degrees Kelvin. K_eq is equal to the product of the concentrations of the reaction products, each raised to the power of their stoichiometry, divided by the product of the substrates, each raised to the power of their stoichiometry:

For the reaction

and for reaction (5)

ΔG⁰ may be calculated from equation (3) if the molar concentrations of substrates and products present at equilibrium are known. If ΔG⁰ is a negative number, K_eq will be greater than unity, and the concentration of products at equilibrium will exceed that of the substrates. If ΔG⁰ is positive, K_eq will be less than unity, and the formation of substrates will be favored.

Note that, since ΔG⁰ is a function exclusively of the initial and final states of the reacting species, it can provide information only about the direction and equilibrium state of the reaction. ΔG⁰ is independent of the mechanism of the reaction and therefore provides no information concerning rates of reactions. Consequently—and as explained below—although a reaction may have a large negative ΔG⁰ or ΔG⁰’, it may nevertheless take place at a negligible rate.

THE RATES OF REACTIONS ARE DETERMINED BY THEIR ACTIVATION ENERGY

Reactions Proceed via Transition States

The concept of the transition state is fundamental to understanding the chemical and thermodynamic basis of catalysis. Equation (7) depicts a group transfer reaction in which an entering group E displaces a leaving group L, attached initially to R:

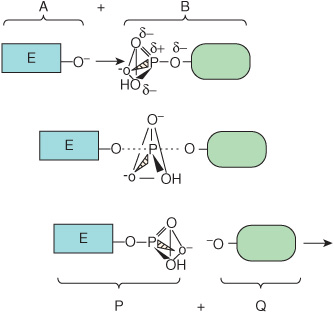
The net result of this process is to transfer group R from L to E. Midway through the displacement, the bond between R and L has weakened but has not yet been completely severed, and the new bond between E and R is yet incompletely formed. This transient intermediate—in which neither free substrate nor product exists—is termed the transition state, E···R···L. Dotted lines represent the “partial” bonds that are undergoing formation and rupture. Figure 8–1 provides a more detailed illustration of the transition state intermediate formed during the transfer of a phosphoryl group.

FIGURE 8–1 Formation of a transition state intermediate during a simple chemical reaction, Shown are three stages of a chemical reaction in which a phosphoryl group is transferred from leaving group L to entering group E. Top: entering group E (A) approaches the other reactant, L-phosphate (B). Notice how the three oxygen atoms linked by the triangular lines and the phosphorus atom of the phosphoryl group form a pyramid. Center: as E approaches L-phosphate, the new bond between E and the phosphate group begins to form (dotted line) as that linking L to the phosphate group weakens. These partially formed bonds are indicated by dotted lines. Bottom: formation of the new product, E-phosphate (P), is now complete as the leaving group L (Q) exits. Notice how the geometry of the phosphoryl group differs between the transition state and the substrate or product. Notice how the phosphorus and three oxygen atoms that occupy the four corners of a pyramid in the substrate and product become coplanar, as emphasized by the triangle, in the transition state.

Reaction (7) can be thought of as consisting of two “partial reactions,” the first corresponding to the formation (F) and the second to the subsequent decay (D) of the transition state intermediate. As for all reactions, characteristic changes in free energy, ΔG_F and ΔG_D are associated with each partial reaction:

For the overall reaction (10), ΔG is the sum of ΔG_F and ΔG_D. As for any equation of two terms, it is not possible to infer from ΔG either the sign or the magnitude of ΔG_F or ΔG_D.

Many reactions involve multiple transition states, each with an associated change in free energy. For these reactions, the overall ΔG represents the sum of all of the free energy changes associated with the formation and decay of all of the transition states. Therefore, it is not possible to infer from the overall ΔG the number or type of transition states through which the reaction proceeds. Stated another way, overall thermodynamics tells us nothing about kinetics.

Δ G_F Defines the Activation Energy

Regardless of the sign or magnitude of ΔG, ΔG_F for the overwhelming majority of chemical reactions has a positive sign. The formation of transition state intermediates therefore requires surmounting energy barriers. For this reason, ΔG_F for reaching a transition state is often termed the activation energy, E_act. The ease—and hence the frequency—with which this barrier is overcome is inversely related to E_act. The thermodynamic parameters that determine how fast a reaction proceeds thus are the ΔG_F values for formation of the transition states through which the reaction proceeds. For a simple reaction, where ∝ means “proportionate to,”

The activation energy for the reaction proceeding in the opposite direction to that drawn is equal to –ΔG_D.

NUMEROUS FACTORS AFFECT THE REACTION RATE

The kinetic theory—also called the collision theory—of chemical kinetics states that for two molecules to react they (1) must approach within bond-forming distance of one another, or “collide,” and (2) must possess sufficient kinetic energy to overcome the energy barrier for reaching the transition state. It therefore follows that anything that increases the frequency or energy of collision between substrates will increase the rate of the reaction in which they participate.

Temperature

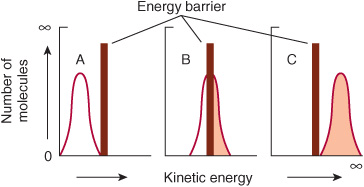
Raising the temperature increases the kinetic energy of molecules. As illustrated in Figure 8–2, the total number of molecules whose kinetic energy exceeds the energy barrier E_act (vertical bar) for formation of products increases from low (A) through intermediate (B) to high (C) temperatures. Increasing the kinetic energy of molecules also increases their rapidity of motion and therefore the frequency with which they collide. This combination of more frequent and more highly energetic, and hence productive, collisions increases the reaction rate.

FIGURE 8–2 The energy barrier for chemical reactions. (See text for discussion.)

Reactant Concentration

The frequency with which molecules collide is directly proportionate to their concentrations. For two different molecules A and B, the frequency with which they collide will double if the concentration of either A or B is doubled. If the concentrations of both A and B are doubled, the probability of collision will increase fourfold.

For a chemical reaction proceeding at constant temperature that involves one molecule each of A and B,

the number of the molecules that possess kinetic energy sufficient to overcome the activation energy barrier will be a constant. The number of collisions with sufficient energy to produce product P therefore will be directly proportionate to the number of collisions between A and B, and thus to their molar concentrations, denoted by the square brackets:

Similarly, for the reaction represented by

which can also be written as

The corresponding rate expression is

or

For the general case, when n molecules of A react with m molecules of B,

the rate expression is

Replacing the proportionality sign with an equals sign by introducing a rate constant k characteristic of the reaction under study gives equations (20) and (21), in which the subscripts 1 and –1 refer to the forward and reverse reactions, respectively:

The sum of the molar ratios of the reactants defines the kinetic order of the reaction. Consider reaction (5). The stoichiometric coefficient for the sole reactant, A, is 2. Therefore, the rate of production of P is proportional to the square of [A] and the reaction is said to be second order with respect to reactant A. In this instance, the overall reaction is also second order. Therefore, k₁ is referred to as a second-order rate constant.

Reaction (12) describes a simple second-order reaction between two different reactants, A and B. The stoichiometric coefficient for each reactant is 1. Therefore, while the overall order of the reaction is 2, it is said to be first order with respect to A and first order with respect to B. In the laboratory, the kinetic order of a reaction with respect to a particular reactant, referred to as the variable reactant or substrate, can be determined by maintaining the concentration of the other reactants at a constant, or fixed, concentration in large excess over the variable reactant. Under these pseudo-first-order conditions, the concentration of the fixed reactant(s) remains virtually constant. Thus, the rate of reaction will depend exclusively on the concentration of the variable reactant, sometimes also called the limiting reactant. The concepts of reaction order and pseudo-first-order conditions apply not only to simple chemical reactions but also to enzyme-catalyzed reactions.

K_eq Is a Ratio of Rate Constants

While all chemical reactions are to some extent reversible, at equilibrium the overall concentrations of reactants and products remain constant. At equilibrium, the rate of conversion of substrates to products therefore equals the rate at which products are converted to substrates:

Therefore,

and

The ratio of k₁ to k_–1 is termed the equilibrium constant, K_eq. The following important properties of a system at equilibrium must be kept in mind.

1. The equilibrium constant is a ratio of the reaction rate constants (not the reaction rates).

2. At equilibrium, the reaction rates (not the rate constants) of the forward and back reactions are equal.

3. Equilibrium is a dynamic state. Although there is no net change in the concentration of substrates or products, individual substrate and product molecules are continually being interconverted.

4. The numeric value of the equilibrium constant K_eq can be calculated either from the concentrations of substrates and products at equilibrium or from the ratio k₁/k_–1.

THE KINETICS OF ENZYMATIC CATALYSIS

Enzymes Lower the Activation Energy Barrier for a Reaction

All enzymes accelerate reaction rates by lowering ΔG_F for the formation of transition states. However, they may differ in the way this is achieved. Where the mechanism or the sequence of chemical steps at the active site is essentially equivalent to those for the same reaction proceeding in the absence of a catalyst, the environment of the active site lowers ΔG_F by stabilizing the transition state intermediates. To put it another way, the enzyme can be envisioned as binding to the transition state intermediate (Figure 8–1) more tightly than it does to either substrates or products. As discussed in Chapter 7, stabilization can involve (1) acid–base groups suitably positioned to transfer protons to or from the developing transition state intermediate, (2) suitably positioned charged groups or metal ions that stabilize developing charges, or (3) the imposition of steric strain on substrates so that their geometry approaches that of the transition state. HIV protease (see Figure 7–6) illustrates catalysis by an enzyme that lowers the activation barrier by stabilizing a transition state intermediate.

Catalysis by enzymes that proceeds via a unique reaction mechanism typically occurs when the transition state intermediate forms a covalent bond with the enzyme (covalent catalysis). The catalytic mechanism of the serine protease chy-motrypsin (see Figure 7–7) illustrates how an enzyme utilizes covalent catalysis to provide a unique reaction pathway.

ENZYMES DO NOT AFFECTK_eq

While enzymes undergo transient modifications during the process of catalysis, they always emerge unchanged at the completion of the reaction. The presence of an enzyme therefore has no effect on ΔG⁰ for the overall reaction, which is a function solely of the initial and final states of the reactants. Equation (25) shows the relationship between the equilibrium constant for a reaction and the standard free energy change for that reaction:

Stay updated, free articles. Join our Telegram channel

Join