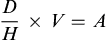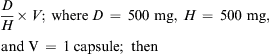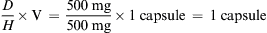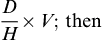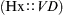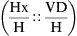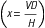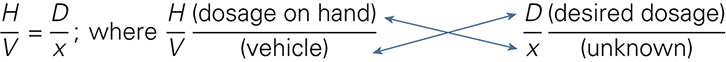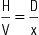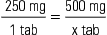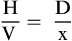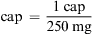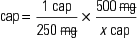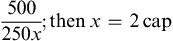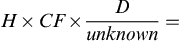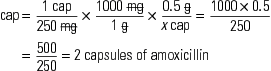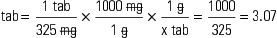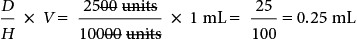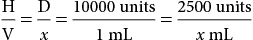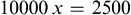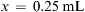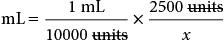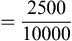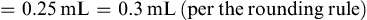http://evolve.elsevier.com/McCuistion/pharmacology
Objectives
• Discuss the metric and household systems of measurement.
• Convert larger units to smaller units and smaller units to larger units within the metric system.
• Convert larger units to smaller units and smaller units to larger units within the household system.
• Convert between metric and household measurements.
Metric System
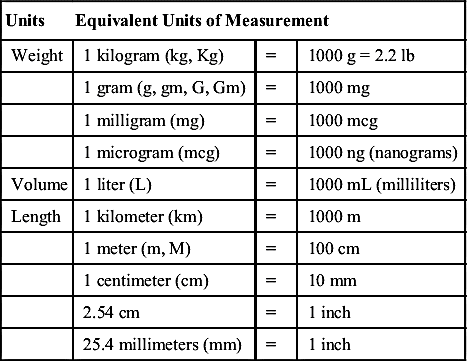
The metric system is a decimal system based on the power of 10. The basic units of measure used in dosage calculations include the gram (g, gm, G, Gm) for weight, liter (L) for volume, and meter (m, M) for linear measurement or length. Prefixes such as nano, micro, milli, centi, and kilo indicate the size of the units in powers of 10 of the base unit and stand for a specific degree of magnitude: for instance, kilo stands for thousands, milli for one thousandth, and centi for one hundredth. To be able to convert a quantity, one of the values must be known, such as a gram (g, G), liter (l, L), meter (m), milligram (mg), milliliter (mL), millimeter (mm), or microgram (mcg). Grams, liters, and meters are larger units, whereas milligrams, milliliters, millimeters, and micrograms are smaller units. Because the conversion between degrees of magnitude always involves multiplying by a power of 10, converting from one magnitude to another is relatively easy.
Conversions Within the Metric System
Common conversions used to calculate drug dosages using the metric system are listed in Table 11A.1.
Grams and milligrams are related by three factors of 10 according to this relationship. In the first illustration below, the larger unit (gram) is converted to the smaller unit (milligram). In the second illustration, the smaller unit is converted to the larger unit.
1g=1mg×103=1000mg
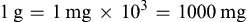
and
1000mg=1 g×10−3=1g
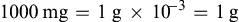
The easiest way to convert larger units to smaller units is to move the decimal point the appropriate number of spaces to the right. In the illustration below, grams have been converted to milligrams by moving the decimal point three spaces to the right:
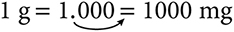
To convert smaller units to larger units, move the decimal point the appropriate number of spaces to the left. In the illustration below, milligrams have been converted to grams by moving the decimal point three spaces to the left (thousandths):
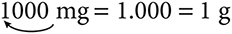
Remember: When changing larger units to smaller units, move the decimal point to the right; when changing smaller units to larger units, move the decimal point to the left. There should always be a zero (0) placed before the decimal point, called a leading zero, to alert the reader that the number is less than 1. For example, 0.5 clearly indicates a value of ½. If the number was to be written as .5, the reader could mistake the number for 5. Do not leave extraneous zeroes after a decimal point (trailing zeroes). The reader may perceive a number that is many times larger than the desired dose. For example, 1.0 could be misread as 10.
Household System
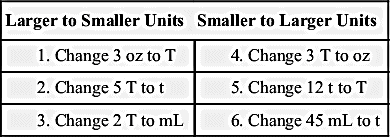
Because of the lack of standardization of spoons, cups, and glasses, household measurement is not as accurate as the metric system, therefore measurements are approximate (Table 11A.2). According to the official U.S. Pharmacopeia, a teaspoon (t) is considered to be equivalent to 5 mL in the metric system. Three teaspoons equal 1 tablespoon (T), therefore 1 T equals 15 mL. Ounces (oz) are fluid ounces in the household measurement system, and there are 2 T in 1 oz therefore 1 ounce equals 30 mL in the metric system.
TABLE 11A.2
| 1 measuring cup | = | 8 oz or 240 mL (1 oz = 30 mL) |
| 1 medium-size glass (tumbler size) | = | 8 oz or 240 mL |
| 1 ounce (oz) | = | 2 tablespoons or 30 mL |
| 1 tablespoon (T) | = | 3 teaspoons or 15 mL |
| 1 teaspoon (t) | = | 60 drops (60 gtt) |
Conversions Within the Household System
When converting larger units to smaller units within the household system, multiply the requested number by the basic equivalent value.
Because household measurements are not as accurate as the metric measurements, instruct patients and caregivers to obtain an approved drug-measuring device to dispense liquid medicine, such as the following:
Answers to Practice Problems
Section 11B
Calculation Methods—Enteral and Parenteral Drug Dosages
Key Terms
basic formula (BF), p. 117
body surface area (BSA), p. 125
body weight (BW), p. 124
controlled substance, p. 114
dimensional analysis (DA), p. 119
drug label, p. 117
fractional equation (FE), p. 118
ratio and proportion (RP), p. 117
square root method, p. 125
trade name, p. 114
units, p. 120
Objectives
• Interpret drug labels.
• Calculate drug dosages using the basic formula, the ratio and proportion/fractional equation method, and the dimensional analysis method.
• Convert all measures to the same system and unit of measure within the system before calculating final drug dosages.
• Calculate drug dosages according to body weight.
• Calculate drug dosages according the body surface area using the West nomogram.
• Calculate drug dosages according the body surface area using the square root method.
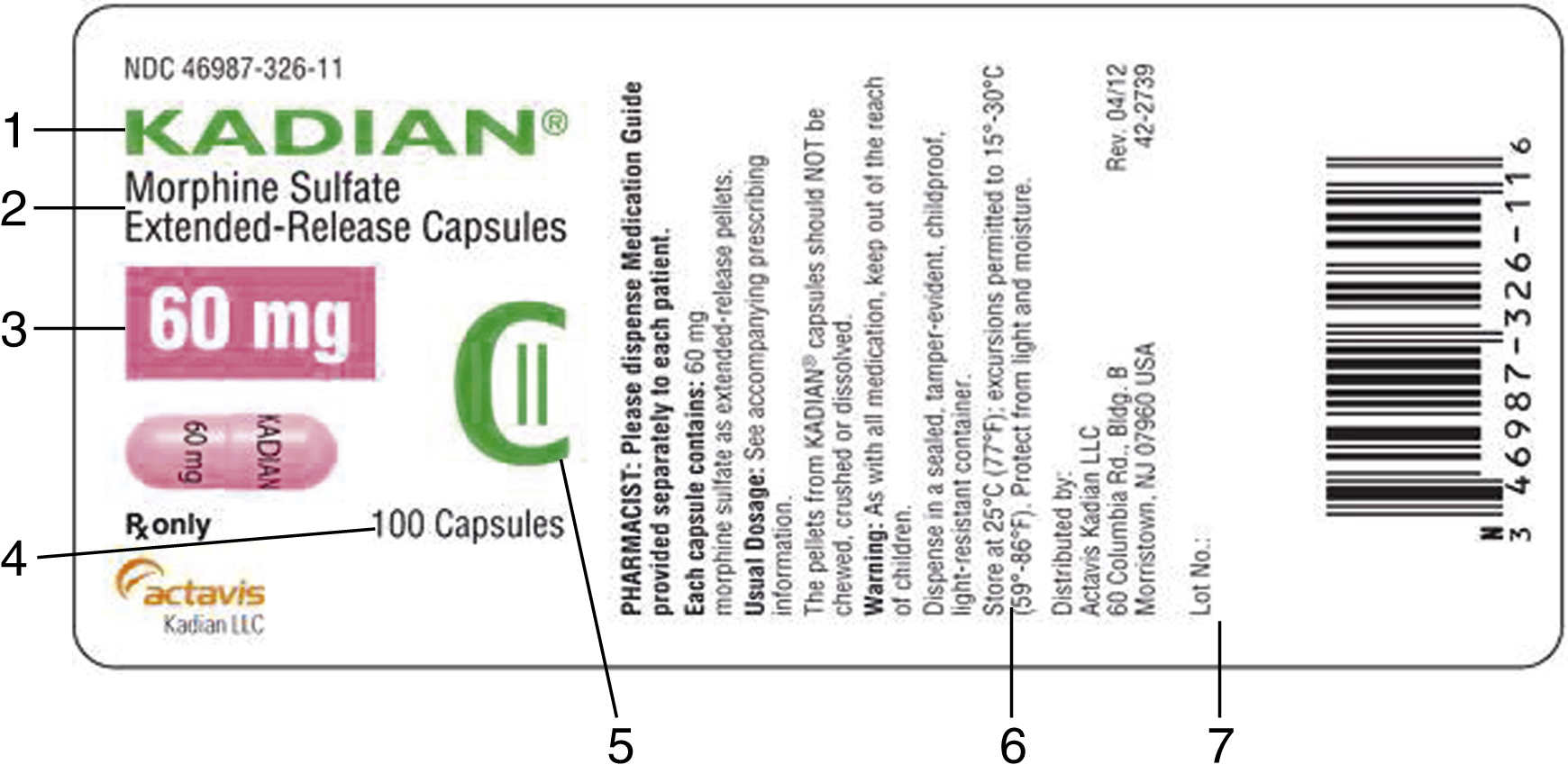
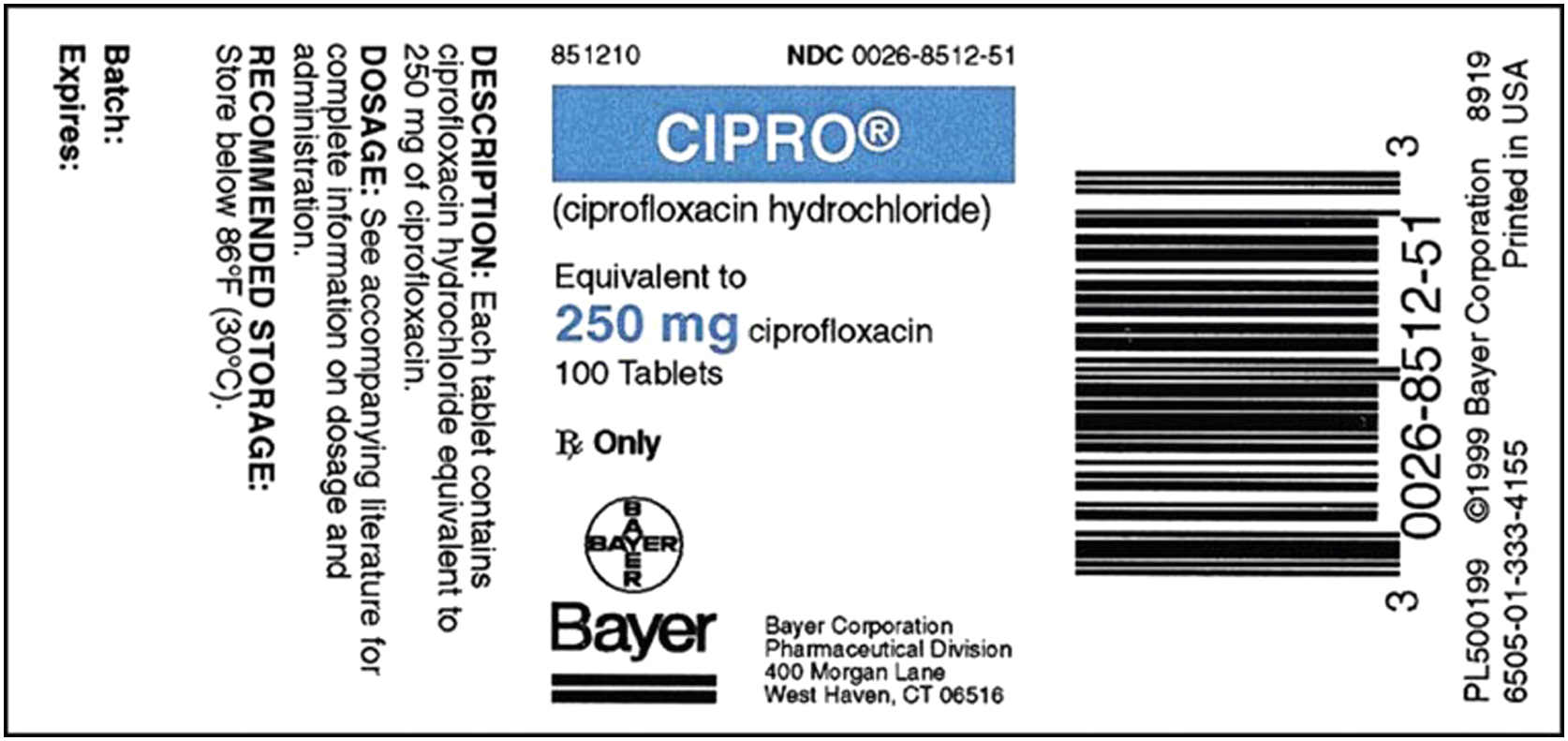
Interpreting Drug Labels
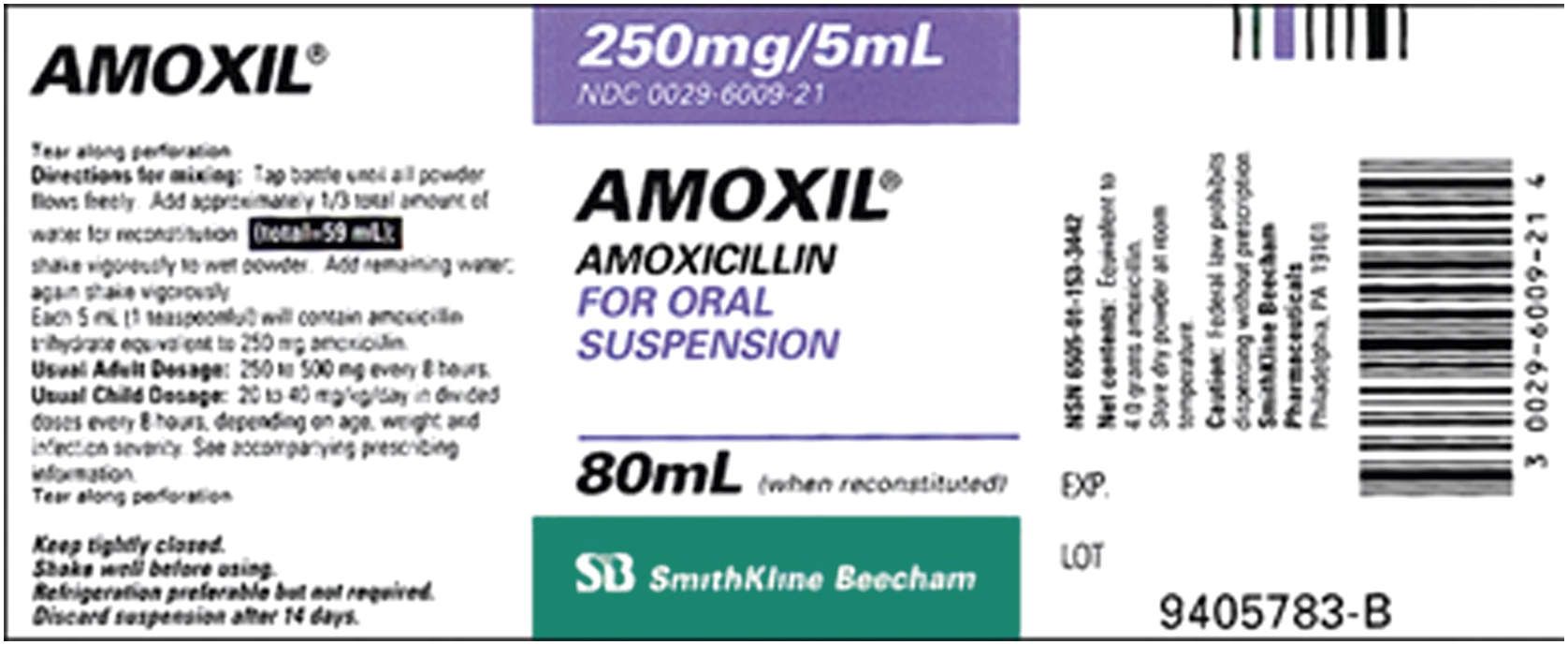
Pharmaceutical companies usually label their drugs with the brand name, also called the trade name, first in large letters with the generic name, then in smaller letters. Labels for generic drugs may have only the generic name of the drug listed. The formulation or the drug amount per tablet, capsule, or unit of liquid (for oral and parenteral doses) is printed on the drug label. Other information found on drug labels includes lot number, expiration date, proper storage of the drug, and whether it is a controlled substance. Two examples of drug labels are given below, the first for an oral drug and the second for a parenteral drug. The third example shows additional information provided on drug labels.
Examples
Interpreting Enteral Drug Labels
1. Tylenol is the brand (trade) name, acetaminophen is the generic name, and the formulation is 500 mg per caplet. That the container holds 100 caplets is irrelevant when calculating the drug dosage.
2. This label lists the generic name only (folic acid). The formulation is 5 mg per mL. There are 10 mL in the vial, which is an irrelevant number when calculating the drug dosage.
3. Kadian1 is the brand (trade) name and morphine sulfate2 is the generic name. The formulation3 is 60 mg per capsule, and the container holds 1004 capsules. It is a schedule II5 drug, which is a controlled substance because of its potential for abuse. The label indicates how the drug is to be stored6, and the lot number7 also appears.
Precautions when Reading Drug Labels
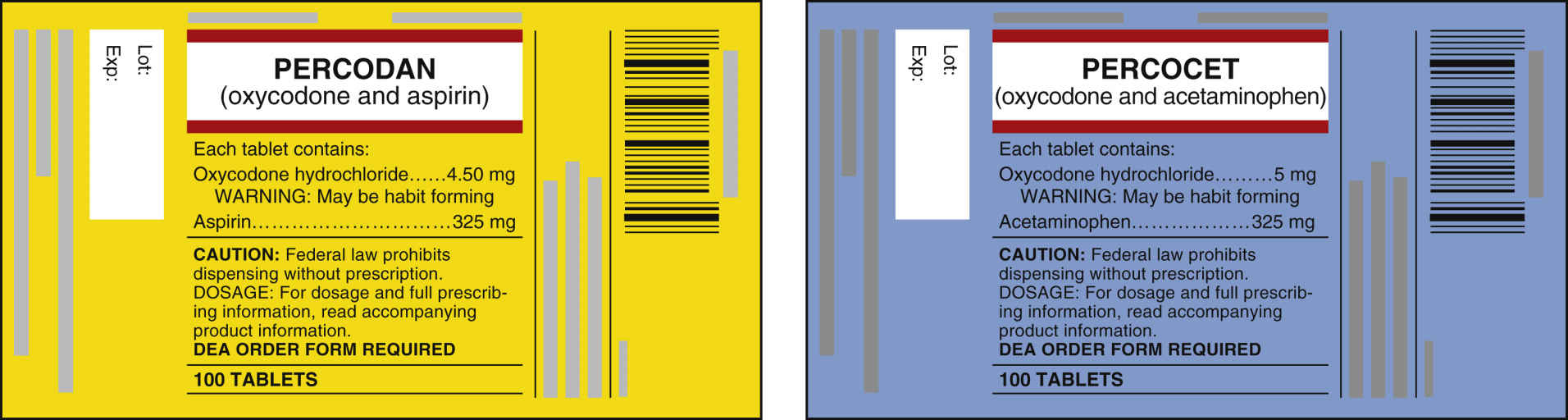
Be aware of drug names that sound or look alike; for example, note the similarity between the trade names Percodan and Percocet. Percocet, which contains oxycodone and acetaminophen, is the preparation most commonly prescribed.
Percodan contains oxycodone and aspirin, and a patient may be allergic to aspirin or should not take aspirin because of a stomach ulcer. Acetaminophen can cause liver toxicity; in persons with normal liver function, the maximum dosage of acetaminophen is 3000 mg per 24 hours.
Note the similarity between quinine sulfate and quinidine gluconate. These drugs differ greatly. Quinine is prescribed for malaria, whereas quinidine is prescribed for cardiac arrhythmias.
To decrease medication errors, the nurse administering the drug should perform a minimum of three label checks with the patient’s medication administration record (MAR).
Practice Problems
Reading Drug Labels
1.
a. What are the generic names? __________________________
b. What are the trade names? ______________________________
c. Is this drug a controlled substance? ____________
d. What is the amount of the drug and the form? _________________
e. How many tablets are in the package? ____________
f. How should this drug be stored? ____________________
2.
a. What is the generic name? __________________________
b. What is the trade name? ______________________________
c. Is this drug a controlled substance? ____________
d. What is the amount of the drug and the form? _________________
e. How many tablets are in the package? ____________
f. How should this drug be stored? ____________________
3.
a. What is the generic name? __________________________
b. What is the trade name? ______________________________
c. Is this drug a controlled substance? ____________
d. What is the concentration of the drug? _________________
e. What is the total volume? ____________
f. How should this drug be stored? ____________________
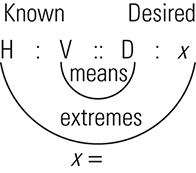
Methods of Drug Calculation
Generally, calculations are made for one dose. For example, if the order states that a patient is to be given 500 mg of a drug three times a day, you would calculate the amount of drug that is equivalent to 500 mg. Occasionally, nurses calculate the full daily dose, which in this case would be 1500 mg (500 mg times three doses).
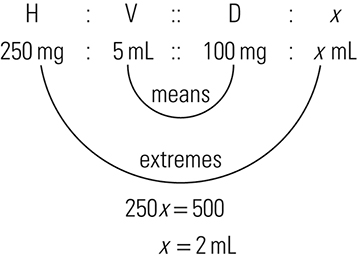
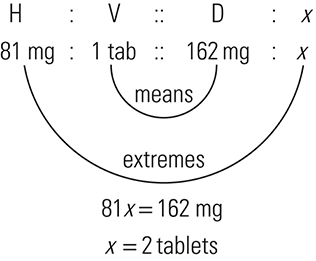
The three general methods for the calculation of drug dosages are the (1) basic formula (BF), (2) ratio and proportion/fractional equation (RP/FE), and (3) dimensional analysis (DA). These methods are used to calculate most enteral and parenteral drug dosages. The nurse should select one of the methods to calculate drug dosages and use that method consistently. All but the dimensional analysis requires using the same units of measure. It is most helpful to convert to the system used on the drug label. If the drug is ordered in grams (g, G) and the drug label gives the dose in milligrams (mg), convert grams to milligrams (the measurement on the drug label) and proceed with the drug calculation.
For drugs that require individualized dosing, calculation by body weight (BW) or by body surface area (BSA) may be necessary. These last two methods are mostly used for the calculation of pediatric dosages and for drugs used in the treatment of cancer (antineoplastic drugs). BW and BSA methods of calculation are also useful for individuals whose BW is low, who are obese, or who are older adults.
Method 1
Basic Formula
The basic formula (BF) is easy to recall:
DH×V=A
Where:
D is the desired dose (as ordered)
H is the drug on hand (available)
V is the vehicle or volume of a drug form (tablet, capsule, liquid [mL])
A is the amount calculated to be given to the patient.
Examples Using the Basic Formula
1. Order: Cefaclor 0.5 g PO bid
Available: Cefaclor 500 mg capsule
How many capsules should the patient receive per dose? (This is a two-step process.)
a. The unit of measure that is ordered (grams) and the unit of measure on the label (milligrams) are from the same system of measurement—the metric system. Conversion to the same unit as on the label is necessary to solve the problem. Because the label is in milligrams, convert grams to milligrams.
To convert grams (large value) to milligrams (smaller value), move the decimal point three spaces to the right as discussed earlier:
b. DH×V;whereD=500 mg,H=500 mg,andV=1capsule; then
DH×V=500mg500mg×1capsule=1capsule
Answer: 500 mg, or 1 tablet
The nurse will administer 1 tablet per dose.
2. Order: Phenobarbital 30 mg PO STAT
Available: Phenobarbital 15 mg per tablet
How many tablets should the patient receive per dose?
The dosage is ordered in milligrams and the unit of measure on the label is also expressed in milligrams. There is no need for conversion.
DH×V;then
30mg15mg×1tablet=2tablets
Answer: 30 mg = 2 tablets
The nurse will administer 2 tablets per dose.
Method 2
Ratio and Proportion/Fractional Equation
Ratio and Proportion: Linear Method
The ratio and proportion (RP) method can be expressed linearly or as a fraction (a fractional equation). The linear setup is as follows:
Where:
D is the desired dose (as ordered)
H is the drug on hand (available)
V is the vehicle or volume of a drug form (tablet, capsule, liquid [mL])
x is the unknown amount to give to the patient
The double colon symbol (::) stands for “as” or “equal to”
Multiply the extremes and the means (Hx∷VD)
. Solve for x HxH∷VDH
; H is the divisor (x=VDH)
.
. Solve for x HxH∷VDH; H is the divisor (x=VDH).Examples Using Ratio and Proportion: Linear Method
1. Order: Amoxicillin 100 mg PO qid
Available: Amoxicillin 250 mg per 5 mL
How many milliliters should the patient receive per dose?
Conversion is not needed because both are expressed in the same unit of measure.
Answer: Amoxicillin 100 mg = 2 mL
The nurse will administer 2 mL per dose.
2. Order: Aspirin 162 mg PO once daily
Available: Aspirin 81 mg per tablet
How many tablets should the patient receive per dose?
Answer: Aspirin 162 mg = 2 tablets
The nurse will administer 2 tablets per dose.
Fractional Equation
The fractional equation (FE) setup is written as a fraction and is more commonly used than the linear setup. This setup will be used to illustrate RP/FE for the rest of this chapter.
Cross-multiply and solve for x, where Hx=VD;thenx=VDH
.
.Examples Using the Fractional Equation—Fraction Method
1. Order: Ciprofloxacin 500 mg PO q12h
Available: Ciprofloxacin 250 mg per tablet
How many tablet(s) should the patient receive per dose?
HV=Dx
Where:
H = 250 mg
V = tablet (tab)
D = 500 mg
x = unknown number of tablets
250mg1tab=500mgxtab
Cross-multiply and solve for x.
250x = 500
x = 2
Answer: 500 mg = 2 tablets
2. Order: Citalopram 10 mg PO once daily
Available: Citalopram 20 mg per tablet
HV=Dx
20mg1tab=10mgxtab
Cross-multiply and solve for x.
20x = 10
x = 0.5 tablet (1/2 tab)
(Note that this tablet is scored to allow it to be split in half.)
Answer: x = 0.5 tablet
The nurse will administer 0.5 tablet per dose.
(For the duration of this chapter, any RP or FE calculation will be shown using the FE method.)
Method 3
Dimensional Analysis
Dimensional analysis (DA) is a calculation method known as units and conversions. The D, H, and V are still used in DA. The advantage of DA is that all the steps for calculating drug dosages are conducted in one equation without having to remember various formulas. However, conversion factors still need to be memorized.
Steps for Dimensional Analysis
1. Identify the unit/form (tablet, capsule, mL) of the drug to be calculated. Place the unit/form to one side of the equal sign (=). This is your desired unit/form.
2. Determine the known dose and unit/form from the drug label that matches the unit/form of the desired dosage. Place this on the other side of the equal sign.
3. Continue with additional fractions using a multiplication operation between each fraction until all but that one unit you want is eliminated.
4. Multiply the numerators and multiply the denominators.
5. Solve for x (the unknown).
Examples Using Dimensional Analysis
1. Order: Amoxicillin 500 mg PO q8h
Available: 250 mg per capsule
How many capsules (cap) will the nurse administer per dose?
a/b. cap=1cap250mg
(H = on-hand)
(H = on-hand)c. Notice that the drug form “cap” to the left of the equal sign is the same as the “cap” in the numerator to the right of the equal sign. (We must determine how many capsules need to be administered for the dose to be 500 mg). The available capsule is 250 mg; this is placed in the denominator.
d. The available strength (250 mg) is the denominator, and the unit/form “mg” must match the next numerator, which is the ordered dose of 500 mg (desired dose). The next denominator would be x cap (unknown) or it would be left blank.
cap=1cap250mg×500mgxcap
e. Cancel out the mg, multiply the numerators, then multiply the denominators.
f. Solve for x by isolating x; reduce the resulting fraction. (Reducing fractions could be done earlier). What remain are cap and 2.
500250x;thenx=2cap
Answer: 2 capsules
When conversions are needed (e.g., between milligrams and grams) a conversion factor (CF) is needed to calculate dosages using the basic formula or RP/FE, requiring a multistep process. When using DA, there should only be the one unknown value in the equation (x). This will be especially important when calculating dosages that involve milligrams per kilogram (mg/kg) or milligrams per meters squared (mg/m2).
2. Order: Amoxicillin 0.5 g PO q8h
Available: 250 mg per capsule
How many capsules will the nurse administer?
A conversion is needed between grams and milligrams. Following the steps for DA, the equation looks like this:
H×CF×Dunknown=
cap=1cap250mg×1000mg1g×0.5gxcap=1000×0.5250=500250=2capsulesofamoxicillin
As with other methods of calculation, the three components are D, H, and V as indicated in the above problem. With dimensional analysis, the conversion factor (CF) is built into the equation and is included when the ordered drug’s unit of measurement and the drug available differ. If the same units of measurement are used, the conversion factor is eliminated from the equation, as shown in the first example.
3. Order: Acetaminophen 1 g PO q6h PRN for headache
Available: Acetaminophen 325 mg per tablet
Conversion factor: 1000 mg = 1 g
How many tablet(s) should be given?
tab=1tab325mg×1000mg1g×1gxtab=1000325=3.07
Answer: 1000 mg [1 g] = 3 tablets
The nurse will administer 3 tablets per dose.
Rounding Rules
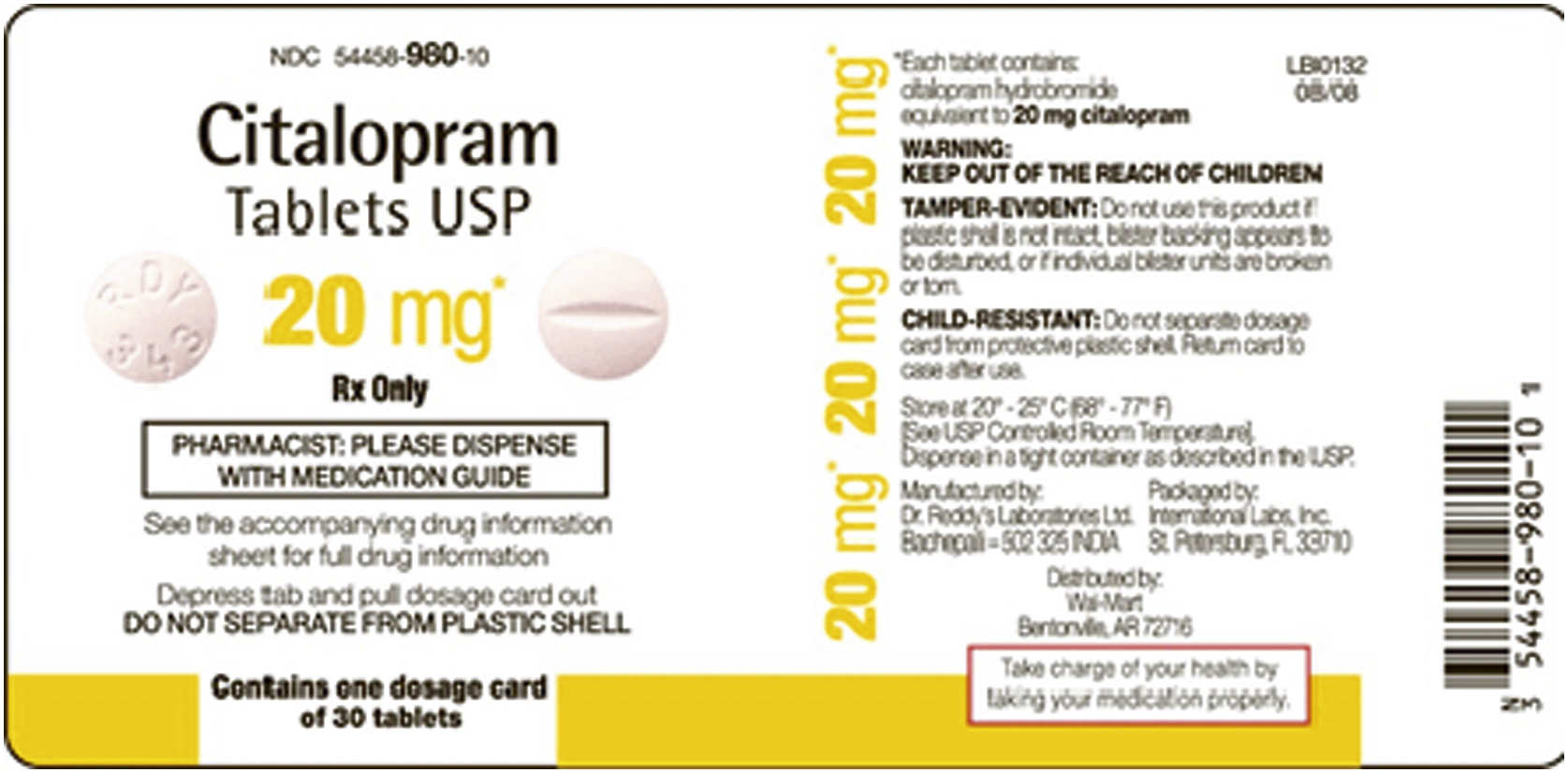
Notice when to round. Tablets and caplets can be rounded to the nearest half if they are scored (see the image for citalopram). Some tablets are scored in fourths. In this case, the dosage can be rounded to the nearest fourth. However, tablets and caplets that are extended release, sustained release, controlled release, or enteric coated should not be split because splitting or crushing these preparations destroys the properties that render the drug long lasting. For this reason, capsules are rounded to the nearest whole number. Liquid drugs can be rounded to the nearest tenth; the exception to this rule is when calculating dosages of drops, which are rounded to the nearest whole number.
When rounding, determine how many places beyond the decimal point are appropriate. The general rounding rules are:
1. If a number to the right of the digit needs to be rounded and is 4 or less, round down. For example, when rounding 1.343 to the hundredth place, the number becomes 1.34. Rounding 1.343 to the tenth place, it becomes 1.3. Rounding 1.343 to a whole number, it becomes 1.
2. If a number to the right of the digit needs to be rounded and is 5 or greater, round up. For example, when rounding 1.745 to the hundredth place, the number becomes 1.75. Rounding 1.745 to the tenth place, it becomes 1.7. Rounding 1.745 to a whole number, it becomes 2.
Calculating Dosages for Drugs Measured in Units or Milliequivalents
Some medications, such as heparin and insulin, are measured in units. Typically, units are not converted into any other measure.
Example
Drug Measured in Units
1. Order: Heparin 2500 units subcut daily
Available: Heparin 10,000 units per mL in a multiple-dose vial (10 mL)
Basic Formula
DH×V=2500units10000units×1mL=25100=0.25mL
Ratio and Proportion/Fractional Equation Methods
HV=Dx=10000units1mL=2500unitsxmL
10000x=2500
Cross-multiply: x=0.25mL
Answer: Heparin 2500 units = 0.25 mL = 0.3 mL
Dimensional Analysis
mL=1mL10000units×2500unitsx
=250010000
=0.25mL=0.3mL(pertheroundingrule)
Electrolytes are often ordered in milliequivalents (mEq). An example is pictured below.
Practice Problems
Enteral and Parenteral Drugs Using Basic Formula, Ratio and Proportion/Fractional Equation, or Dimensional Analysis
1. Order: Ranitidine 150 mg PO q12h
Available: Ranitidine 75 mg per tablet
2. Order: Doxycycline 100 mg PO q12h
Available: Doxycycline 100 mg capsules
Administer how many capsules per dose? _________________
3. Order: Warfarin 2 mg PO once daily
Available: Warfarin 2 mg tablets
Administer how many tablets per dose? _________________
4. Order: Hydrochlorothiazide 12.5 mg PO every morning
Available: Hydrochlorothiazide 25 mg tablets
Administer how many tablets per dose? __________________
5. Order: Furosemide 20 mg IM STAT
Available: Furosemide 10 mg per mL
Administer how many milliliters per dose? __________________
6. Ordered: Atropine sulfate 0.4 mg subcut STAT
Available: Atropine sulfate 1 mg per mL
Administer how many milliliters for the STAT dose? ____________________
(There could be a point of confusion with this label. The concentration is 1 mg/mL in each vial, and there are 25 vials in the package.)
7. Ordered: Lactulose solution 20 g by mouth tid
Available: Lactulose solution 10 g per 15 mL
Administer how many milliliters per dose? _________
8. Ordered: Phenytoin oral solution 0.25 g PO bid
Available: Phenytoin oral solution 125 mg per 5 mL
9. Order: Heparin 7500 units subcut now; 3500 units subcut daily
Available: 5000 units per mL single-dose vial
a. Administer how many milliliters for the now dose? ______________
b. Administer how many milliliters for the daily dose? _____________
c. How many vial(s) of heparin are needed? ________________
