Dosage regimens
John H. Collett and Soraya Dhillon
Chapter contents
Dosage regimens: influence on the plasma concentration-time profile of a drug in the body
One-compartment open model of drug disposition in the body
Rate of drug input versus rate of drug output
Elimination rate constant and biological half-life of a drug
Concentration-time curve of a drug in the body following the oral administration of equal doses of a drug at fixed time intervals
Important factors influencing steady-state plasma concentrations of a drug
Dose size and frequency of administration
Population data and basic pharmacokinetic parameters
Influence of changes in the apparent elimination rate constant of a drug: patients with renal impairment
Key points
Dosage regimens: influence on the plasma concentration-time profile of a drug in the body
The design of a dosage regimen determines the therapeutic benefit for patients. The principles of clinical pharmacokinetics are applied to design a dosage regimen for a patient that ensures the appropriate formulation of drug is chosen for an appropriate route of administration. On the basis of the patient’s drug handling parameters, which require an understanding of absorption, distribution, metabolism and excretion, the dosage regimen for the medicine in a particular patient, can be optimized. The pharmacist needs to ensure the appropriate regimen is prescribed to achieve optimal efficacy and minimal toxicity.
Clinical pharmacokinetics provides a basic understanding of the principles required to design a dosage regimen. Pharmacokinetics provides a mathematical basis to assess the time course of drugs and their concentrations in the body. It enables the following processes to be quantified:
It is these four pharmacokinetic processes, often referred to as ADME, that determine the drug concentration in the body following administration of a medicine (see also Chapter 18).
The influence that physiological factors, physicochemical properties of a drug and dosage form factors can have in determining whether a therapeutically effective concentration of a drug is achieved in the plasma following oral administration of a single dose of drug has been discussed previously in Chapters 19 and 20.
Whilst a single dose of certain drugs, e.g. single-dose hypnotics, analgesics and antiemetics, may be used in some clinical situations, most medicines are given as a multiple dosage regimen. For example, for the treatment of a respiratory tract infection, amoxicillin may be prescribed as one 250 mg capsule three times a day. The design of the regimen, i.e. formulation, route of administration, dose size and the dosage frequency are important factors which influence what plasma concentration is achieved and maintained in the body over the prescribed course of drug treatment. Other factors to consider are: patient choice and lifestyle, including the route of administration (the oral route is often preferred by patients), the dosing interval (once, twice or three times a day) needs to be suitable for a patient’s work pattern and the dosage form must be appropriate, for instance a liquid may be preferable to a capsule for young and elderly patients.
Rates of ADME processes
To describe the processes of ADME, there is a need to consider the rates of the various processes. In zero-order reactions, the reaction proceeds at a constant rate and is independent of the concentration of a substance present in the body. An example is the elimination of alcohol. Drugs exhibiting this type of elimination will show accumulation of plasma levels of the drug, and hence non-linear pharmacokinetics. In first-order reactions, the reaction proceeds at a rate which is dependent on the concentration of a drug in the body. Most ADME processes follow first-order kinetics (Chapter 7).
The majority of drugs used clinically at therapeutic dosages will show first-order rate processes, e.g. the rate of elimination of most drugs will be first order. However, some drugs show non-linear rates of elimination, for instance phenytoin and high dose salicylates. First-order rate processes do not result in accumulation, i.e. as the amount of drug administered increases, the body is able to eliminate the drug accordingly. Hence, if the dose is doubled, the steady-state plasma concentration is doubled. Whether a drug shows first- or zero-order elimination is determined by its Michaelis Constant (Km). This parameter is the plasma concentration at which the elimination of the drug proceeds at half the maximum metabolic capacity (Vm). If normal therapeutic plasma levels of the drug exceed the drug’s Michaelis Constant, then the drug will show non-linear drug handling. For most drugs, the Michaelis Constant is much higher than the levels achieved through normal therapeutic use.
One-compartment open model of drug disposition in the body
To understand how the design of a dosage regimen can influence the time course of a drug in the body, as measured by its plasma concentration-time profile, it is important to consider the complex pharmacokinetic processes of: drug input (i.e. administration); output (i.e. elimination/metabolism) and distribution within the body. This can be described using the one-compartment open model of drug disposition, shown in Figure 22.1.
Pharmacokinetic models are hypothetical constructs, which describe the fate of a drug in a biological system following its administration. The purpose of modeling is to characterize the ADME profile for a drug to indicate how the drug is handled by the patient and to characterize basic parameters. These basic parameters describe the fate of the drug following administration and are used to optimize a dosage regimen. In a one-compartment model, the drug is considered to be distributed instantly throughout the whole body following its release and absorption from the dosage form. Thus, the body behaves as a single compartment in which absorbed drug is distributed so rapidly that a concentration equilibrium exists at any given time between the plasma, other body fluids and the tissues into which the drug has become distributed.
Rate of drug input versus rate of drug output
In a one-compartment open model, the overall kinetic processes of drug input and drug output are described by first-order kinetics. Following administration of an oral dosage form, the process of drug input into the body compartment involves drug release from the dosage form and passage of drug (absorption) across the cellular membranes, in this case the gastrointestinal barrier. The rate of drug input (absorption) at any given time is proportional to the concentration of drug, which is assumed to be in an absorbable form, in solution in the gastrointestinal fluids at the site(s) of absorption, i.e. the effective concentration, Ce, of drug at time, t.
Hence:
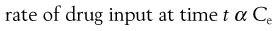 (22.1)
(22.1)
and
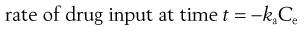 (22.2)
(22.2)
where ka is the apparent absorption rate constant.
The negative sign in Equation 22.2 indicates that the effective concentration of drug at the absorption site(s) decreases with time. The apparent absorption rate constant gives the proportion (or fraction) of drug which enters the body compartment per unit time. Unlike the rate of drug input into the body compartment, the apparent absorption rate constant, ka, is independent of the effective concentration of drug at the absorption site(s). The rate of drug input will decrease gradually with time as the effective drug concentration at the site of absorption decreases (assumes first-order absorption). Other processes, such as chemical degradation and movement of drug away from the absorption site(s), will also contribute to the gradual decrease in the drug concentration with time at the absorption site.
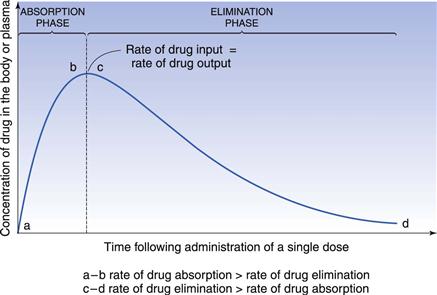
In the case of a one-compartment open model, the rate of drug output or elimination is a first-order process. Consequently, the magnitude of this parameter at any given time is dependent on the concentration of drug in the body compartment at that time. Immediately following administration of the first dose of an oral dosage form, the rate of drug output from the body, i.e. elimination, will be low since a limited amount of drug has been absorbed into the body compartment. However, as absorption proceeds, initially at a higher rate than the rate of drug output, the net concentration of drug in the body will increase with time. As the rate of drug output from the body compartment increases whilst the rate of drug input into the body compartment is decreasing with time, there will be a point at which the rate of drug input is equal to the rate of drug output, such that the net concentration of drug in the body compartment will reach a peak value (Cmax) and then begin to fall with time. At this stage, the rate of drug output exceeds the rate of drug input.
These changes in the rates of drug input and output, relative to each other, with time are responsible for the characteristic shape of the concentration-time course of a drug in the body shown in Figure 22.2 following oral administration of a single dose of a drug.
The shape of the curve is determined by the relationship between the rate of absorption and the rate of elimination. The greater the rate of drug input relative to the rate of drug output from the body compartment over the net absorption phase, the higher will be the peak concentration achieved in the body or plasma following oral administration of a single dose of drug. This explains why increases in dose size and formulation changes in dosage forms, which produce increases in the effective concentration of drug at the absorption site(s), result in higher peak plasma and body concentrations being obtained for a given drug. It should also be noted that any unexpected decrease in the rate of drug output relative to the rate of drug input, which may occur as the result of renal impairment or poor drug metabolism, is also likely to result in higher plasma and body concentrations of drug than expected, and the possibility of the patient exhibiting toxicity. The adjustment of dosage regimens in cases of patients having severe renal impairment is considered later.
Elimination rate constant and biological half-life of a drug
In the case of a one-compartment open model, the rate of elimination or output of a drug from the body compartment follows first-order kinetics and is related to the concentration of drug, Ct, remaining in the body compartment at time t, by the following equation:
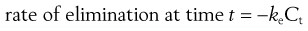 (22.3)
(22.3)
where ke is the apparent elimination rate constant. The negative sign in Equation 22.3 indicates that elimination is removing drug from the body compartment.
The apparent elimination rate constant of a drug gives the proportion, or fraction, of that drug which is eliminated from the body per unit time. Its units are in terms of time−1. The apparent elimination constant of a given drug thus provides a quantitative index of the persistence of that drug in the body.
For example the fraction of drug remaining after time t is calculated from:
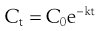 (22.4)
(22.4)
where 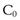 is the starting concentration. e−kt is the fraction of drug remaining and the fraction eliminated is given by:
is the starting concentration. e−kt is the fraction of drug remaining and the fraction eliminated is given by:
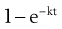 (22.5)
(22.5)
Application of these equations is shown in Box 22.1.
An alternative parameter used is the biological or elimination half-life of the drug, t1/2
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree



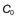 , of 16 mg/L, then at 4 hours the fraction remaining in the body (Ct) is equal to
, of 16 mg/L, then at 4 hours the fraction remaining in the body (Ct) is equal to 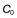 e−kt. Thus:
e−kt. Thus: