Dissolution and solubility
Michael E. Aulton
Chapter contents
Solution, solubility and dissolution
Energy/work changes during dissolution
Dissolution rates of solids in liquids
Factors affecting the rate of dissolution
Measurement of dissolution rates of drugs from dosage forms
Methods of expressing solubility and concentration
Solubility of solids in liquids
Solubility of gases in liquids
Solubility of liquids in liquids
Distribution of solutes between immiscible liquids
Solubility of solids in solids
Key points
Introduction
Solutions are encountered frequently in pharmaceutical development, either as a dosage form in their own right or as a clinical trials material. Additionally, almost all drugs function in solution in the body.
This chapter discusses the principles underlying the formation of solutions from solute and solvent and the factors that affect the rate and extent of the dissolution process. This process will be discussed particularly in the context of a solid dissolving in a liquid as this is the situation most likely to be encountered in the formation of a drug solution, either during manufacturing or during drug delivery.
Further properties of solutions are discussed in Chapter 3 and 24. Because of the number of principles and properties that need to be considered, the contents of each of these chapters should only be regarded as introductions to the various topics. The student is encouraged, therefore, to refer to the bibliography cited at the end of each chapter in order to augment the present contents. The textbook written by Florence & Attwood (2011) is recommended particularly. It uses a large number of pharmaceutical examples to aid in the understanding of physicochemical principles.
Definition of terms
This chapter will begin by clarifying some of the key terms relevant to solutions.
Solution, solubility and dissolution
A solution may be defined as a mixture of two or more components that form a single phase that is homogeneous down to the molecular level. The component that determines the phase of the solution is termed the solvent; it usually (but not necessarily) constitutes the largest proportion of the system. The other component(s) are termed solute(s) and these are dispersed as molecules or ions throughout the solvent, i.e. they are said to be dissolved in the solvent.
The transfer of molecules or ions from a solid state into solution is known as dissolution. Fundamentally, this process is controlled by the relative affinity between the molecules of the solid substance and those of the solvent. The extent to which the dissolution proceeds under a given set of experimental conditions is referred to as the solubility of the solute in the solvent. The solubility of a substance is the amount of it that passes into solution when equilibrium is established between the solute in solution and the excess (undissolved) substance. The solution that is obtained under these conditions is said to be saturated. A solution with a concentration less than that at equilibrium is said to be subsaturated. Solutions with a concentration greater than equilibrium can be obtained in certain conditions; these are known as supersaturated solutions.
Since the above definitions are general ones, they may be applied to all types of solution involving any of the three states of matter (gas, liquid, solid) dissolved in any of the three states of matter, i.e. solid-in-liquid, liquid-in-solid, liquid-in-liquid, solid-in-vapour, etc. However, when the two components forming a solution are either both gases or both liquids, then it is more usual to talk in terms of miscibility rather than solubility. Other than the name, all principles are the same.
One point to emphasize at this stage is that the rate of solution (dissolution rate) and amount which can be dissolved (solubility) are not the same and are not necessarily related. In practice, high drug solubility is usually associated with a high dissolution rate, but there are exceptions; an example is the commonly used film-coating material hydroxypropyl methylcellulose (HPMC) which is very water soluble yet takes many hours to hydrate and dissolve.
Process of dissolution
Dissolution mechanisms
The majority of drugs and excipients are crystalline solids. Liquid, semi-solid and amorphous solid drugs and excipients do exist but these are in the minority. For now, we will restrict our discussion to dissolution of crystalline solids into liquid solvents. Also, to simplify the discussion, it will be assumed that the drug is molecular in nature. The same discussion applies to ionic drugs. Again, to avoid undue repetition in the explanations that follow, it can be assumed that most solid crystalline materials, whether drugs or excipients, will dissolve in a similar manner.
The dissolution of a solid in a liquid may be regarded as being composed of two consecutive stages.
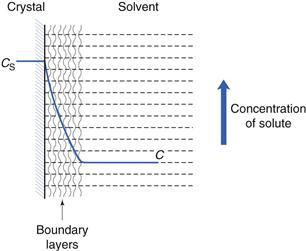
These stages, and the associated solution concentration changes, are illustrated in Figure 2.1.
These two stages of dissolution are now discussed in turn.
Interfacial reaction
Leaving the surface.
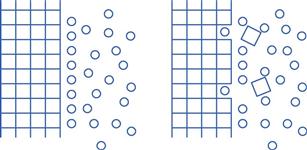
Dissolution involves the replacement of crystal molecules by solvent molecules. This is illustrated in Figure 2.2.
The process of the removal of drug molecules from a solid, and their replacement by solvent molecules, is determined by the relative affinity of the various molecules involved. The solvent/solute forces of attraction must overcome the cohesive forces of attraction between the molecules of the solid.
Moving into the liquid.
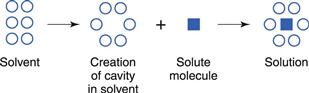
On leaving the solid surface, the drug molecule must become incorporated in the liquid phase, i.e. within the solvent. Liquids are thought to contain a small amount of so-called ‘free volume’. This can be considered to be in the form of ‘holes’ that, at a given instant, are not occupied by the solvent molecules themselves (this point is discussed further in Chapter 3). Individual solute molecules are thought to occupy these ‘holes’, as shown in Figure 2.3.
The process of dissolution may be considered, therefore, to involve the relocation of solute molecules from an environment where they are surrounded by other identical molecules, with which they form intermolecular attractions, into a cavity in a liquid where they are surrounded by non-identical molecules, with which they may interact to different degrees.
Diffusion through the boundary layer
This step involves transport of the drug molecules away from the solid/liquid interface into the bulk of the liquid phase under the influence of diffusion or convection. Boundary layers are static or slow-moving layers of liquid that surround all solid surfaces that are surrounded by liquid (discussed further later in this chapter and in Chapter 6). Mass transfer takes place more slowly (usually by diffusion; Chapter 3) through these static or slow-moving layers that inhibit the movement of solute molecules from the surface of the solid to the bulk of the solution. The solution in contact with the solid will be saturated (because it is in direct contact with undissolved solid). During diffusion, the concentration of the solution in the boundary layers changes from being saturated (CS) at the crystal surface to being equal to that of the bulk of the solution (C) at its outermost limit, as shown in Figure 2.1.
Energy/work changes during dissolution
In order for the process of dissolution to occur spontaneously at a constant pressure, the accompanying change in free energy or Gibbs free energy (ΔG) must be negative. The free energy (G) is a measure of the energy available to the system to perform work. Its value decreases during a spontaneously occurring process until an equilibrium position is reached when no more energy can be made available, i.e. ΔG = 0 at equilibrium.
In most cases heat is absorbed when dissolution occurs and the process is usually defined as an endothermic one. In some systems, where marked affinity between solute and solvent occurs, the overall enthalpy change becomes negative so that heat is evolved and the process is an exothermic one.
Dissolution rates of solids in liquids
Like any reaction that involves consecutive stages, the overall rate of dissolution will be dependent on which of these steps is the slowest (the rate-determining or rate-limiting step). In dissolution, the interfacial step (as described above) is virtually instantaneous and so the rate of dissolution will most frequently be determined by the rate of the slower step of diffusion of dissolved solute through the static boundary layer of liquid that exists at a solid/liquid interface. On the rare occasions when the release of the molecule from the solid into solution is slow and the transport across the boundary layer to the bulk solution is faster, dissolution is said to be interfacially controlled.
The rate of diffusion will obey Fick’s Law of Diffusion. Fick’s Law states that the rate of change in concentration of dissolved material with time is directly proportional to the concentration difference between the two sides of the diffusion layer, i.e.:
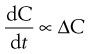 (2.1)
(2.1)
or
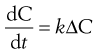 (2.2)
(2.2)
where C is the concentration of solute in solution at any point and at time t, and the constant k is the rate constant (s−1). The energy difference between the two concentration states provides the driving force for the diffusion.
In the present context, ΔC is the difference in concentration of solution at the solid surface (C1) and the bulk of the solution (C2). At equilibrium, the solution in contact with the solid (C1) will be saturated (concentration = CS) as discussed above. Thus ΔC = C1 − C2 = CS − C.
If C2 is less than saturated, the molecules will move from the solid to the bulk (as during dissolution). If the concentration of the bulk (C2) is greater than this, the solution is referred to as supersaturated and movement of solid molecules will be in the direction of bulk solution to surface (as occurs during crystallization).
An equation known as the Noyes–Whitney equation was developed to define the dissolution from a single spherical particle. This equation has found great usefulness in the estimation or prediction of the dissolution rate of pharmaceutical particles. The rate of mass transfer of solute molecules or ions through a static diffusion layer (dm/dt) is directly proportional to the area available for molecular or ionic migration (A), the concentration difference (ΔC) across the boundary layer and is inversely proportional to the thickness of the boundary layer (h).
This relationship is shown in Equation 2.3 and in a slightly modified form in Equation 2.4.
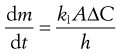 (2.3)
(2.3)
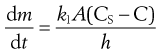 (2.4)
(2.4)
The constant k1 is known as the diffusion coefficient. It is commonly given the symbol D and has the units of m2/s.
If the volume of the solvent is large, or solute is removed from the bulk of the dissolution medium by some process at a faster rate than it passes into solution, then C remains close to zero and the term (CS – C) in Equation 2.4 may be approximated to CS. In practice, if the volume of the dissolution medium is so large that C is not allowed to exceed 10% of the value of CS, then the same approximation may be made. In either of these circumstances dissolution is said to occur under ‘sink’ conditions and Equation 2.4 may be simplified to:
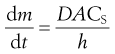 (2.5)
(2.5)
Sink conditions may arise in vivo when a drug is absorbed into the body from its solution in the gastrointestinal fluids at a faster rate than it dissolves in those fluids from a solid dosage form, such as a tablet. The phrase is illustrative of the solute molecules ‘disappearing down a sink’!
If solute is allowed to accumulate in the dissolution medium to such an extent that the above approximation is no longer valid, i.e. when C > (CS/10), then ‘non-sink’ conditions are said to be in operation. When C builds up to such an extent that it equals CS, i.e. the dissolution medium is saturated with solute, it is clear from Equation 2.4 that the overall rate of dissolution will be zero.
Factors affecting the rate of dissolution
The various factors that affect the in vitro rate of diffusion-controlled dissolution of solids into liquids can be predicted by examination of the Noyes–Whitney equation (Eqns 2.3 or 2.4). Most of the effects of these factors are included in the summary given in Table 2.1.
Table 2.1
Factors affecting in-vitro dissolution rates of solids in liquids
| Term in Noyes–Whitney equation (Eqn 2.4) | Affected by |
| A: surface area of undissolved solid (Rate of dissolution increases proportionally with increasing A) | Size of solid particles (A increases with particle size reduction) Dispersibility of powdered solid in dissolution medium Porosity of solid particles |
| CS: saturated solubility of solid in dissolution medium (Rate of dissolution increases proportionally with increasing difference between CS and C. Thus high CS speeds up dissolution rate) | Temperature Nature of dissolution medium Molecular structure of solute Crystalline form of solid Presence of other compounds |
| C: concentration of solute in solution at time t (Rate of dissolution increases proportionally with increasing difference between CS and C. Thus low C speeds up dissolution rate) | Volume of dissolution medium (increased volume decreases C) Any process that removes dissolved solute from the dissolution medium (hence decreasing C) |
| k: dissolution rate constant | Diffusion coefficient D of solute in the dissolution medium Viscosity of medium |
| h: thickness of boundary layer (Rate of dissolution decreases proportionally with increasing boundary layer thickness) | Degree of agitation of dissolution medium (increased agitation decreases boundary layer thickness). |
Clearly, increases in those factors on the top of the right-hand side of the Noyes–Whitney equation will increase the rate of diffusion (and therefore rate of dissolution) and increases in factors at the bottom of the equation will result in a decreased rate of dissolution. The opposite situation obviously applies regarding a reduction in these parameters. Each of these is discussed briefly below.
Surface area of undissolved solid (A)
Size of solid particles.
The surface area of isodiametric particles is inversely proportional to their particle size. Much practical evidence exists to show that, in general, milling or other means of particle size reduction will increase the rate of dissolution of sparingly soluble drugs. An added complication is that particle size will change during the dissolution process, because large particles will become smaller and small particles will eventually disappear. This effect is shown in Figure 2.4.
Compacted masses of solid may also disintegrate into smaller particles, thus increasing the surface area available for dissolution as the disintegration process progresses. (This effect is shown in Figure 30.7 and explained further in the associated discussion.)
Dispersibility of powdered solid in dissolution medium.
If solid particles form cohered masses in the dissolution medium, then the surface area available for dissolution is reduced. This effect may be overcome by the addition of a wetting agent to improve the dispersion of the solid into primary powder particles.
Porosity of solid particles.
Pores in some materials, particularly granulated ones, may be large enough to allow access of the dissolution medium and outward diffusion of dissolved solute molecules.
Solubility of solid in dissolution medium (CS)
Temperature.
Dissolution may be an exothermic or an endothermic process and so temperature changes will influence the energy balance and thus the energy available to promote dissolution.
Nature of dissolution medium.
Factors such as solubility parameters, pH and presence of cosolvents will affect the rate of dissolution.
Molecular structure of solute.
Factors such as the use of salts of either weakly acidic or weakly basic drugs, or esterification of neutral compounds, can influence solubility and dissolution rate.
Crystalline form of solid.
The presence of polymorphs, hydrates, solvates or the amorphous form of the drug can all have an influence on dissolution rate.
Presence of other compounds.
The common-ion effect, complex formation and the presence of solubilizing agents can affect the rate of dissolution.
Concentration of solute in solution at time t (C)
Volume of dissolution medium.
If the volume of the dissolution medium is small, C can rapidly increase during dissolution and approach CS. If the volume is large, then C may be negligible with respect to CS and thus ‘sink’ conditions will operate. This can be controlled in vitro but must be taken into account in vivo as the volume of the stomach contents can vary greatly (hence the common instruction ‘To be taken with a glass of water’). Also, the volume of the fluid in the rectum and vagina is small (see Chapter 42) and so this consideration can be important in drug delivery from suppositories and pessaries.
Any process that removes dissolved solute from the dissolution medium.
For example, adsorption on to an insoluble adsorbent, partitioning into a second liquid that is immiscible with the dissolution medium, removal of solute by dialysis or by continuous replacement of solution by fresh dissolution medium can result in a decrease in C and thus an increased rate of dissolution.
Dissolution rate constant (k)
Thickness of the boundary layer.
This is affected by the degree of agitation, which in turn depends on the speed of stirring or shaking, shape, size and position of stirrer, volume of dissolution medium, shape and size of container, and viscosity of dissolution medium.
Diffusion coefficient of solute in the dissolution medium.
The diffusion coefficient of solute in the dissolution medium is affected by the viscosity of the dissolution medium, and the molecular characteristics and size of diffusing molecules.
It should be borne in mind that pharmaceutical scientists are often concerned with the rate of dissolution of a drug from a formulated product such as a tablet or a capsule, as well as with the dissolution rates of pure solids. In practice, the rate of dissolution can have either zero-order, first-order, second-order or cube-root kinetics. These are discussed later in the book when relevant to particular dosage forms. Later chapters in this book can also be consulted for information on the influence of formulation factors on the rates of release of drugs into solution from various dosage forms.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree