TERMS
•Alligation
•Alligation alternate
•Alligation medial
•Diluent
•Stock solution
OBJECTIVES
Upon completion of this chapter, the technician student will be able to:
•Describe the relationship of active ingredients and diluents if the amount of active ingredient remains constant and the amount of diluent is increased or decreased.
•Determine the percent strength and ratio strength of a given product when the active ingredient remains constant and the amount of diluent is increased or decreased.
•Determine the volume of solution of a desired strength given a specified quantity of any given strength.
•Determine the volume of a specified stock solution needed to prepare a given solution.
•Determine the quantity of an active ingredient in a specified amount of solution needed to prepare a given solution.
•Define the alligation methods of problem solving.
•Use the alligation methods (alligation alternate and alligation medial) to determine the percent strength of alcohol mixtures.
•Use the alligation methods (alligation alternate and alligation medial) to determine relative amounts of components mixed together to make a mixture of a required strength.
Chapter 9 addresses problems arising from the quantitative relationship between specific ingredients and the pharmaceutical preparation as a whole. This chapter introduces problems of a slightly different character: those that arise when pharmaceutical preparations are diluted (by the addition of diluent or by admixture with solutions or mixtures of lower strength) or are concentrated (by the addition of active ingredient or by admixture with solutions or mixtures of greater strength).
diluent A substance added to a pharmaceutical product to reduce its strength, or dilute it. A diluent most often has no drug substance in it; examples are sterile water and petrolatum.
Problems such as these sometimes seem complicated and difficult. Solving some of these calculations requires a series of steps. Understanding the basic concepts of dilution and concentration uncomplicates these problems.
Many problems can be solved in several ways. The best way is not necessarily the shortest: the best way is the one that is clearly understood and that leads to the correct answer.
Rules to Simplify the Calculation

These two rules, wherever they may be applied, greatly simplify the calculation:
1. When ratio strengths are given, convert them to percentage strengths before setting up a proportion. It is much easier to solve using a decimal or percent, like 10 (%):0.2 (%) than a fraction represented by the ratio like 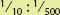 .
.
2.Whenever proportional parts enter into a calculation, reduce them to lowest terms. Instead of calculating with a ratio like 25 (parts):75 (parts), simplify it to 1 (part):3 (parts).
 Relationship Between Strength and Total Quantity
Relationship Between Strength and Total Quantity
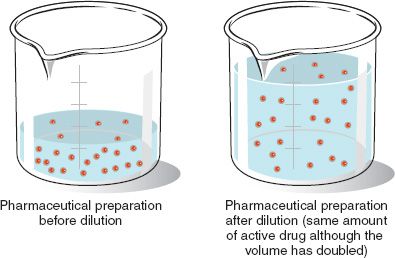
If a mixture of a given percentage or ratio strength is diluted to twice its original quantity, its active ingredient will be contained in twice as many parts of the whole, and its strength therefore will be reduced by one-half. So if 50 mL of a solution containing 10 g of active ingredient with a strength of 20% or 1:5 w/v is diluted to 100 mL, the original volume is doubled, but the original strength is now reduced by one-half to 10% or 1:10 w/v.
If, then, the amount of active ingredient remains constant, any change in the quantity of a solution or mixture of solids is inversely proportional to the percentage or ratio strength; that is, the percentage or ratio strength decreases as the quantity increases, and vice versa. In other words, if the amount of active ingredient remains the same and the volume gets larger, the concentration gets smaller. Likewise, if the amount of active ingredient remains the same and the volume gets smaller, the concentration increases.
This relationship is generally true except for volume-in-volume and weight-in-volume solutions containing components that contract when mixed together. It is not possible to add the volume of ingredients and get the total volume of the final product in all cases. It is possible when mixing solids.
Problems in this chapter generally may be solved by one of the following methods:
1.Inverse proportion:
![]()
where C = concentration and Q = quantity.
2.The following formula:
![]()
That is,
![]()
3.Determining the quantity of active constituent (solute) needed and then calculating the quantity of the available solution (usually concentrated or stock solution) that will provide the needed amount of constituent.
For most situations the student technician is encouraged to use the formula method of solving these dilution and concentration problems. Sometimes the third method is the easiest of the three, usually when the strength of the product is very small and the technician is using a prepared strength available in a vial or ampul. Examples of these are detailed later in the chapter. In the formula method the second quantity and second concentration are always that of the final product, not of the active ingredient or diluent.
 Dilution and Concentration of Liquids
Dilution and Concentration of Liquids
Determination of Percentage or Ratio Strength
Calculating the percentage or ratio strength of a solution made by diluting or concentrating (by evaporation) a solution of given quantity and strength entails the following.
Examples:
If 500 mL of a 15% v/v solution of methyl salicylate in alcohol is diluted to 1500 mL, what is the percentage strength v/v?
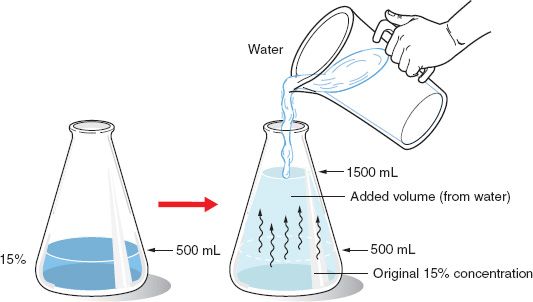
![]()
500(mL) × 15(%) = 1500(mL) × X(%)
X = 5%, answer
Solve by Inverse Proportion:
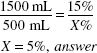
Calculate the Active Ingredient:
500 mL of 15% v/v solution contains 75 mL of methyl salicylate (active ingredient).
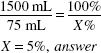
If 50 mL of a 1:20 w/v solution of aluminum acetate is diluted to 1000 mL, what is the ratio strength w/v?
1:20 = 5%
![]()
50 (mL) × 5 (%) = 1000 (mL) × (%)
X = 0.25% = 1:400, answer
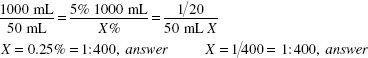
Calculate the Active Ingredient:
50 mL of a 1:20 solution contains 2.5 g of aluminum acetate.
Critical Thinking 10.1

Dilution of a solid or liquid does not entail adding more drug. Therefore, the amount of drug in the diluted product is the same; only the volume is larger.
If a cup of coffee is too strong for a person’s taste, the person may add water to dilute it. No additional coffee is used.
Determining Amount of Solution of a Desired Strength
Calculating the amount of solution of a desired strength that can be made by diluting or concentrating (by evaporation) a specified quantity of a solution of given strength involves the following.
Examples:
How much 10% w/w (in grams) ammonia solution can be made from 1800 g of 28% w/w strong ammonia solution?
![]()
1800 (g) × 28 (%) = X(g) × 10%
X = 5040 g, answer
Solve by Inverse Proportion:
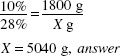
Calculate the Active Ingredient:
1800 g of 28% ammonia water contains 504 g of ammonia (100%).
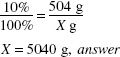
How much (in milliliters) of a 1:5000 w/v solution of phenylmercuric acetate can be made from 125 mL of a 0.2% solution?
1:5000 = 0.02%
![]()
125 (mL) × 0.2 (%) = X (mL) × 0.02 (%)
X = 1250 mL, answer
Solve by Inverse Proportion:
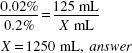
Or
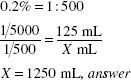
Calculate the Active Ingredient:
125 mL of a 0.2% solution contains 0.25 g of phenylmercuric acetate
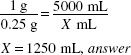
 Stock Solutions
Stock Solutions
Stock solutions are solutions of known concentration that are prepared by the pharmacist or technician for convenience in dispensing. They are usually strong solutions from which weaker ones may be made conveniently. When correctly prepared, these solutions enable the pharmacist to obtain small quantities of medicinal substances that are to be dispensed in solution.
stock solution A solution of a known concentration prepared for the convenience of dispensing; usually a strong solution from which weaker ones can be made conveniently.
Stock solutions usually are prepared on a weight-in-volume basis, and their concentration is expressed as a ratio strength or less frequently as a percentage strength.
Amount of Solution Needed to Prepare Desired Solution
Calculating the amount of a solution of given strength that must be used to prepare a solution of desired amount and strength involves the following.
Examples:
How much (in milliliters) of a 1:400 w/v stock solution should be used to make 4 L of a 1:2000 w/v solution?
4 L = 4000 mL
1:400 = 0.25% 1:2000 = 0.05%
![]()
X (mL) × 0.25% = 4000 mL × 0.05(%)
X = 800 mL, answer
Solve by Inverse Proportion:
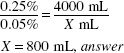
Or
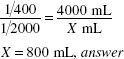
Calculate the Active Ingredient:
4000 mL of a 1:2000 w/v solution requires 2 g of active constituent (solute), thus:
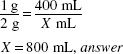
How much (in milliliters) of a 1:400 w/v stock solution should be used in preparing 1 gal of a 1:2000 w/v solution?
1 gal = 3785 mL
1:400 = 0.25% 1:2000 = 0.05%
![]()
X × 0.25% = 3785 (mL) × 0.05(%)
X = 757 mL, answer
Solve by Inverse Proportion:
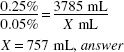
Calculate the Active Ingredient:
To make 1 gal of a 1:2000 w/v solution requires 1.89 g of active constituent, thus:
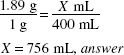
How much (in milliliters) of a 1% stock solution of a certified red dye should be used in preparing 4000 mL of a mouthwash that is to contain 1:20,000 w/v of the certified red dye as a coloring agent?
1:20,000 = 0.05%
![]()
X × 1(%) = 4000 (mL) × 0.005 (%)
X = 20 mL, answer
Solve by Inverse Proportion:
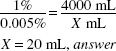
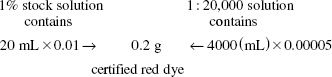
Calculate the Active Ingredient:
To make 4000 mL of a 1:20,000 w/v solution requires 0.2 g of certified red dye, thus:
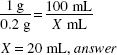
How much (in milliliters) of a 1:50 stock solution of ephedrine sulfate should be used in compounding the following prescription?

1:50 = 2%
![]()
X × 2 (%) = 30 (mL) × 0.25 (%)
X = 3.75 mL, answer
Solve by Inverse Proportion:
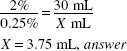
Calculate the Active Ingredient:
30 (g) × 0.0025 = 0.075 g of ephedrine sulfate needed
1:50 means 1 g in 50 mL of stock solution.
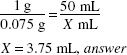
Using a Stock Vial or Ampuls
Sometimes it is necessary to make a specified concentration of a product so dosing will be easier for the patient. These are most often products that are available in vials or ampuls with concentrations in milligrams per milliliter or micrograms per milliliter. Many injectable products are mixed to physician-ordered concentrations to be given orally.
When using small volumes and low-concentration products, it is usually easier to use the same method to calculate the amount of drug (stock) and diluent as to calculate the amount of active ingredient, since these products are not labeled in percent or ratio strength, but in milligrams per milliliter or micrograms per milliliter.
Examples:
Prepare 30 mL of a 5 mg/mL oral phenobarbital solution using phenobarbital available from the manufacturer in a 65 mg/mL solution that comes in 1-mL vials. How much stock solution will be required?
30(mL) × 5 mg/mL = 150 mg required for the solution.
![]()
Or
5 mg/mL = 0.005 g/mL, a 0.5% solution
65 mg/mL = 0.065 g/mL = 6.5% solution
![]()
X × 6.5 (%) = 30 (mL) × 0.5 (%)
X = 2.3 mL of phenobarbital, answer
Folic acid is available from the manufacturer in a 5 mg/mL injection. Prepare 1 oz of 25 mEq/mL oral solution. How much folic acid solution is required?
1 oz = 30 mL
30 (mL) × 25 mEq/mL = 750 mEq to make the solution.
750 mEq = 0.75 mg
Or
5 mg/mL = 0.005 g/mL, a 0.5% solution.
25 mEq/mL = 0.000025 g/mL = 0.0025% solution.
![]()
X × 0.5 (%) = 30 (mL) × 0.0025 (%)
X = 0.15 mL of folic acid, answer
Hydrocortisone is available in a vial of 100 mg in 2 mL. You are to prepare 24 mL of a 5-mg/mL hydrocortisone dilution using the available stock vials. How much hydrocortisone (in milliliters) and how much diluent (in milliliters) will you need?
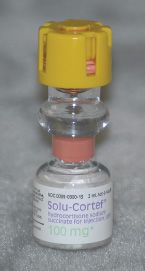
Or
5 mg/mL = 0.005 g/mL, a 0.5% solution
100 mg/2 mL = 0.1 g/2 mL, a 5% solution
![]()
X × 5 (%) = 24 (mL) × 0.5 (%)
X = 2.4 mL hydrocortisone, answer
24 mL – 2.4 mL = 21.6 mL diluent, answer
Review Set 10.1: Stock Solutions
1.If 250 mL of a 1:800 v/v solution is diluted to 1000 mL, what will be the ratio strength v/v?
2.Aluminum acetate topical solution contains 5% w/v aluminum acetate. When 100 mL is diluted to 1 L, what will be the ratio strength w/v?
3.If 400 mL of a 20% w/v solution is diluted to 2 L, what will be the percentage strength w/v?
4.If a 0.067% w/v methylbenzethonium chloride lotion is diluted with an equal volume of water, what will be the ratio strength w/v of the dilution?
5.How much 40% solution is needed to make 500 mL of a 5% solution?
6.How much of a 1:80 solution is needed to make 500 mL of a 0.02% solution?
7.How much of a 0.06% topical solution is required to make 200 mL of a 1:10,000 solution?
8.Folic acid is available from the manufacturer in vials of 5 mg in 1 mL. Prepare 30 mL of a folic acid dilution in a 100 mcg/mL concentration. How much folic acid (in milliliters) do you need?
9.Hydrocortisone is available in a concentration of 100 mg/2 mL from the manufacturer. You are to prepare 10 mL of a 15-mg/mL preparation. How much hydrocortisone do you need?
10.How much diluent (in milliliters) must be added to 180 mL of a 40% solution to make a 5% solution?
11.A solution of potassium permanganate is prepared by dissolving 16 tablets of 0.2 g in enough purified water to make 1600 mL.
a.What is the percentage strength of the solution?
b.What is the ratio strength of the solution?
12.Potassium iodide oral solution, USP, contains 1 g/mL of potassium iodide. How much of the solution (in millimeters) should be used to obtain the potassium iodide required in compounding the prescription below?

13.Clindamycin is available in a solution of 150 mg/mL. How much of this solution is required to make 15 mL of a clindamycin ophthalmic injection 1 mg/0.1 mL?
14.In preparing a solution for a wet dressing, two 0.3-g tablets of potassium permanganate are dissolved in 1 gal of purified water. What will be the percentage strength w/v of the solution?
15.If 150 mL of a 17% w/v concentrate of benzalkonium chloride is diluted to 5 gal, what will be the ratio strength w/v of the dilution?
16.What is the strength of a sodium chloride solution obtained by evaporating 800 g of a 10% w/w solution to 250 g?
17.A physician prescribes an ophthalmic suspension to contain 100 mg of cortisone acetate in 8 mL of normal saline solution. The pharmacist has on hand a 2.5% suspension of cortisone acetate in normal saline solution. How much (in milliliters) of this and how much normal saline solution (in milliliters) should be used in the prescribed suspension?





