TERMS
•Daily dose
•Dosage regimen
•Dose
•Loading dose
OBJECTIVES
Upon completion of this chapter, the technician student will be able to:
•Convert units of measurement to the same system and same units.
•Correctly calculate the number of tablets or capsules or amount of solution or suspension needed to deliver a prescribed dose or dosage regimen.
•Correctly calculate the volume necessary to deliver a prescribed dose or therapeutic regimen.
•Correctly calculate the days or doses a given supply will last.
•State a ratio-proportion to solve a given dosage calculation.
•Solve dosage calculations with ratio-proportion.
•Solve dosage calculation with a stated formula.
•Solve dosage calculation with dimensional analysis.
This chapter focuses on dosage calculations relevant to the dispensing of prefabricated medications, particularly on those for normal adult doses. Prefabricated products and dosage units are used in filling prescriptions and medication orders in the pharmacy. On a small scale, many hospital pharmacies and some community pharmacies manufacture bulk quantities of a limited number of products for use in their pharmacies. Such medications include those administered orally, vaginally, rectally, and topically.
Drug doses vary greatly between drug substances; some drugs have small doses, and other drugs have relatively large doses. The dose of a drug is based on its biochemical and pharmacologic activity; its physical and chemical properties, such as the dosage form and the route of administration; and various patient factors. The dose of a drug for a particular patient may be determined in part by the patient’s age, weight, body surface area, disease state, and liver and kidney function (for drug metabolism and elimination).
dose The amount of drug administered to or taken by a patient.
Drugs intended to produce systemic effects must be absorbed or delivered directly to the circulation and distributed in adequate concentrations to the body’s cellular sites of action.
Drug use and dose information are provided in the package label and inserts that accompany manufacturers’ pharmaceutical products, as well as in a variety of references, such as Facts and Comparisons,1 Physicians’ Desk Reference,2 Pediatric Dosing Handbook,3 Geriatric Dosage Handbook,4 Drug Information Handbook,5 and USP DI.6
One of the primary responsibilities of a pharmacy technician is to gather information about the patient and receive the prescription order from the patient or medication order from the nursing unit. If a dose varies widely from the usual dose, usual dose range, or dosage regimens of the medicine prescribed, the pharmacist must be alerted. The pharmacist is ethically bound to consult the physician to make certain that the dose as written or interpreted is the dose intended and that it is suitable for the patient and condition being treated.
dosage regimen The schedule of dosing, or length of time the drug is taken, e.g., 1 tablet 4 times a day for 10 days.
Doses of oral tablets and capsules are expressed by the number of tablets or capsules taken. Many tablets are scored in halves (Fig. 6.1) and even fourths to make dividing doses easy for the patient. When calculating doses for prefabricated oral tablets or capsules, it is preferred to dispense the fewest number of tablets or capsules whenever there is a choice of strengths. Only scored tablets are intended to be divided; breaking or cutting of unscored tablets may result in a medication error, resulting in an underdose or overdose of medication.
Figure 6.1 These tablets are scored in half.
For the patient, liquid dosage is usually measured in household terms, most commonly by the teaspoonful and tablespoonful. In calculating doses, pharmacists and physicians accept a capacity of 5 mL for the teaspoonful and 15 mL for the tablespoonful. The capacities of household teaspoons vary from 3 to 7 mL, and those of tablespoons vary from 15 to 22 mL. Such factors as viscosity and surface tension of a given liquid and the technique of the person measuring the liquid can influence the actual volume held by a household spoon. Chapter 4 discusses devices for measuring liquid medication formulations.
Calculation of Doses
Rules for Calculating Doses
Step 1.Convert. Be sure all of the measurements are in the same system and all units are the same. It is preferable to convert to the system of measurement used for the medication on hand.
Step 2.Think. Estimate a reasonable amount that should be given.
Step 3.Calculate the drug dose with one of the three methods shown.
Step 4.Dispense the fewest number of tablets or capsules whenever there is a choice of strengths.
Step 1 means that prescription and/or medication orders written and supplied in the same system but in different units must be converted to the same units. For example, an order written in the metric system will be supplied in the metric system: the order is written in grams, and the supply is in milligrams. It is most practical to convert to the smaller unit (grams to milligrams), since this normally eliminates the decimal. Often, it is necessary to convert household and apothecaries’ measures to the metric system. The metric system is preferred in the practice of pharmacy.
Solving Using Ratio-Proportion Method
Step 1. Convert if necessary.
Be sure all measures are in the same system and that all units are the same. It is usually easiest to convert to the unit of measure that is on the drug label (or the available quantity).
Step 2. State the ratio.
•The known ratio is stated first, using what is on hand (the information obtained from the drug label). The unknown ratio (what is desired or ordered) is second.
•The terms of the ratios in a proportion must be written in the same order: mg : tab :: mg : tab or mg : mL :: mg : mL or mg/tab = mg/tab
Another way to express this is
where H = dose on hand; Q = quantity on hand (number of tablets, capsules, or milliliters); D = desired dose; and X = unknown quantity.
•Label all answers
Chapter 1 explains that a ratio is an expression of the relative magnitude of two like quantities and a proportion expresses the equality of two ratios. Following the definition in Chapter 1, the ratios should be expressed as mg : mg :: tab : tab.
Or
This equation is equivalent to the previous one, because the first mathematical step in solving for X is cross-multiplication, and both equations result in H × X = Q × D. These equations are equal, and therefore the ratio can be expressed in terms of what is on hand in proportion to the prescribed dose (the unknown ratio).
Example:
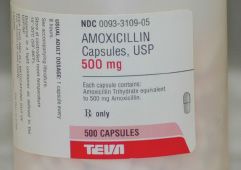
Ordered: 2 g of amoxicillin
Available: amoxicillin 500-mg capsules
How much is to be given per dose?
Step 1. Convert grams to milligrams (move decimal 3 places to the right).
2 g = 2000 mg
Or
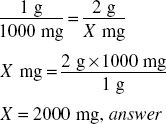
Step 2. Estimate.
Solving for X: cross-multiply.
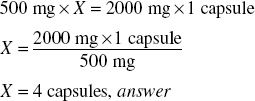
Critical Thinking 6.1
Does your answer make sense? Is this a reasonable amount? Anytime you arrive at an answer that gives you a large number of tablets or capsules (more than four in this case), check your work!
Example:
Ordered: Lactulose® Syrup 20 g tid
Available: Lactulose® 10 g/15 mL syrup
How much is to be given per dose?
Step 1: No conversion necessary.
Step 2: Estimate.
Step 3: Calculate.
Solve for X
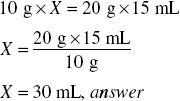
Household Measure Rule
Remember to give the patient directions in household measure.
15 mL = 1 tbs = ½ oz
30 mL = 2 tbs = 1 oz
Examples:
Ordered: Lopressor® 100 mg po bid
Available: Lopressor® 50 mg
Step 1: No conversion necessary.
Step 2: Estimate.
Step 3: Calculate dose.
Cross-multiply.
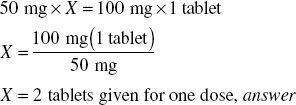
Ordered: diazepam 12.5 mg PO
Available: diazepam 2-, 5-, and 10-mg tablets, all scored in half
Step 1: No conversion necessary.
Step 2: Estimate.
Step 3: Calculate dose.
For the diazepam 2-mg tablets:
It takes 6¼ 2-mg tablets to give one 12.5-mg dose.
For the diazepam 5-mg tablets:
It takes 2½ 5-mg tablets to give one 12.5 mg dose.
For the 10-mg tablets:
It takes 1¼ tablets to give one 12.5-mg dose.
Remember step 4 of the rules for calculating doses: dispense the fewest number of tablets. The tablets are scored in half; therefore, giving either of the strengths requiring one-fourth of a tablet would not give the patient an accurate dose. Therefore, it is correct to dispense the 5-mg tablets, instructing the patient to take 2½ tablets per dose.
Solving Using a Formula
where D = desired dose; H = dose on hand (information on label); Q = quantity on hand (number of tablets, capsules, or mL); X = unknown amount to give.
This formula is based on the ratio-proportion method covered in the previous section. Remember the ratio:
Cross-multiply and simplify:
Step 1.Convert if necessary; must have the same units and systems of measure.
Step 2.Estimate. Think. Do not rely solely on formulas; use critical thinking to estimate a reasonable answer and avoid errors.
Step 3.Calculate.
Examples:
Ordered: Levaquin® 0.5 g po daily
Available: Levaquin® 250-mg tablets
Step 1. Convert 0.5 g to milligrams by moving the decimal three places to the right.
0.5 g = 500 mg
Step 2. Estimate.
Step 3. Calculate.
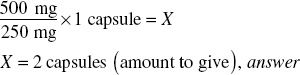
Ordered: 0.3 mg SQ of drug A
Available: 1000 mcg/2 mL of drug A
Step 1. Convert 0.3 mg to micrograms (available strength of drug A).
0.3 mg = 300 mcg
Step 2. Estimate.
Step 3. Calculate.
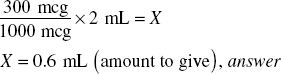
Solving Using Dimensional Analysis
The dimensional analysis method uses three factors. First is the drug factor, the form of the drug dose with its equivalence in units. For example, 1 tablet = 250 mg. Second is the conversion factor; for example, 1 g = 1000 mg; 1 teaspoonful = 5 mL. Third is the drug order factor, the desired dosage. Use these three factors to set up the equation. When it is set up correctly, all of the labels cancel from both the numerator and the denominator except the label that is desired in the answer.
Examples:
Ordered: Xanax® 2 mg
Available: Xanax® 0.5 mg
No conversion necessary.
Estimate.
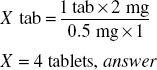
Ordered: penicillin VK 600,000 units
Available: penicillin VK 400,000 units in scored tablets
How many tablets = 600,000 units?
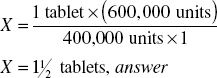
Ordered: kanamycin 1 g po q 6h × 3 days
Available: kanamycin 500-mg capsules
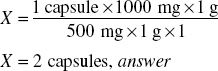
Rules for Calculating Oral Doses of Tablets and Capsules
1.The maximum number of tablets or capsules to administer per dose is usually three. Recheck your calculations and order for more than this.
2.Before calculating the dose, make sure that the dose ordered and what is available are in the same system of measurement and the same unit. If conversion is necessary, convert to the unit and system available.
3.No more than 10% variation should exist between the dose ordered and the dose administered.
4.It does not matter by which method the dose is calculated. It is important to develop the ability to think critically about what is a reasonable amount.
5.State the dose as what the patient is going to take. For example, 0.5 tablets should be expressed as ½ tablet.
6.Dispense the strength allowing the patient to take the fewest whole tablets or capsules. If the dose cannot be taken in whole tablets, remember that scored tablets are the ones intended to be broken.
