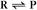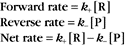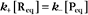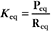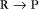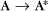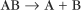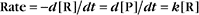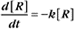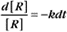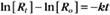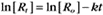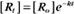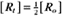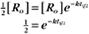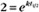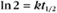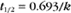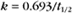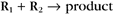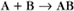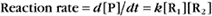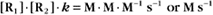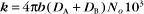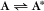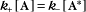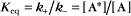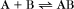Biophysical Principles

CHAPTER 4 Biophysical Principles^*

The concepts in this chapter form the basis for understanding all the molecular interactions in chemistry and biology. To illustrate some of these concepts with a practical example, the chapter concludes with a section on an exceptionally important family of enzymes that bind and hydrolyze the nucleotide GTP. This example provides the background knowledge to understand how GTPases participate in numerous processes covered in later chapters.

Most molecular interactions are driven by diffusion of reactants that simply collide with each other on a random basis. Similarly, dissociation of molecular complexes is a random process that occurs with a probability determined by the strength of the chemical bonds holding the molecules together. Many other reactions occur within molecules or molecular complexes. The aim of biophysical chemistry is to explain life processes in terms of such molecular interactions.

The extent of chemical reactions is characterized by the equilibrium constant; the rates of these reactions are described by rate constants. This chapter reviews the physical basis for rate constants and how they are related to the thermodynamic parameter, the equilibrium constant. These simple but powerful principles permit a deeper appreciation of molecular interactions in cells. On the basis of many examples presented in this book, it will become clear to the reader that rate constants are at least as important as equilibrium constants, since the rates of reactions govern the dynamics of the cell. The chapter includes discussion of the chemical bonds important in biochemistry. Box 4-1 lists key terms used in this chapter.

BOX 4-1 Key Biophysical Terms

Rate constants, designated by lowercase ks, relate the concentrations of reactants to the rate of a reaction.

Equilibrium constants are designated by uppercase Ks. One important and useful concept to remember is that the equilibrium constant for a reaction is related directly to the rate constants for the forward and reverse reactions, as well as the equilibrium concentrations of reactants and products.

The rate of a reaction is usually measured as the rate of change of concentration of a reactant (R) or product (P). As reactants disappear, products are formed, so the rate of reactant loss is directly related to the rate of product formation in a manner determined by the stoichiometry of the mechanism. In all the reaction mechanisms in this book, the arrows indicate the direction of a reaction. In the general case, the reaction mechanism is expressed as

Reaction rates are expressed as follows:

At equilibrium, the forward rate equals the reverse rate:

and concentrations of reactants R_eq and products P_eq do not change with time.

The equilibrium constant K is defined as the ratio of the concentrations of products and reactants at equilibrium:

so it follows that

In specific cases, these relationships depend on the reaction mechanism, particularly on whether one or more than one chemical species constitute the reactants and products. The equilibrium constant will be derived from a consideration of the reaction rates, beginning with the simplest case in which there is one reactant.

First-Order Reactions

First-order reactions have one reactant (R) and produce a product (P). The general case is simply

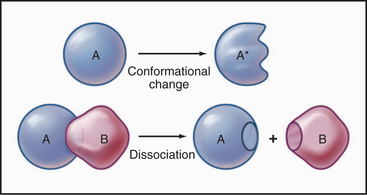
Some common examples of first-order reactions (Fig. 4-1) include conformational changes, such as a change in shape of protein A to shape A^*:

Figure 4-1 first-order reactions. In first-order reactions, a single reactant undergoes a change. In these examples, molecule A changes conformation to ^* and the bimolecular complex AB dissociates to A and B. The rate constant for a first-order reaction (arrows) is a simple probability.

and the dissociation of complexes, such as

The rate of a first-order reaction is directly proportional to the concentration of the reactant (R, A, or AB in these examples). The rate of a first-order reaction, expressed as a differential equation (rate of change of reactant or product as a function of time [t]), is simply the concentration of the reactant times a constant, the rate constant k, with units of s⁻¹ (pronounced “per second”):

The rate of the reaction has units of M s⁻¹, where M is moles per liter and s is seconds (pronounced “molar per second”). As the reactant is depleted, the rate slows proportionally.

A first-order rate constant can be viewed as a probability per unit of time. For a conformational change, it is the probability that any A will change to ^* in a unit of time. For dissociation of complex AB, the first-order rate constant is determined by the strength of the bonds holding the complex together. This “dissociation rate constant” can be viewed as the probability that the complex will fall apart in a unit of time. The probability of the conformational change of any particular A to ^* or of the dissociation of any particular AB is independent of its concentration. The concentra-tions of A and AB are important only in determining the rate of the reaction observed in a bulk sample (Box 4-2).

BOX 4-2 Relationship of the Half-Time to a First-Order Rate Constant

In thinking about a first-order reaction, it is sometimes useful to refer to the half-time of the reaction. The half-time, t_1/2, is the time required for half of the existing reactant to be converted to product. For a first-order reaction, this time depends only on the rate constant and therefore is the same regardless of the starting concentration of the reactant. The relationship is derived as follows:

Thus, integrating, we have

where R_o is the initial concentration and R_t is the concentration at time t. Rearranging, we have

When the initial concentration R_o is reduced by half,

so, rearranging, we have

Therefore, a first-order rate constant can be estimated simply by dividing 0.7 by the half-time. Clearly, an analogous calculation yields the half-time from a first-order rate constant. This relationship is handy, as one frequently can estimate the extent of a reaction without knowing the absolute concentrations, and this relationship is independent of the extent of the reaction at the outset of the observations.

To review, the rate of a first-order reaction is simply the product of a constant that is characteristic of the reaction and the concentration of the single reactant. The constant can be calculated from the half-time of a reaction (Box 4-2).

Second-Order Reactions

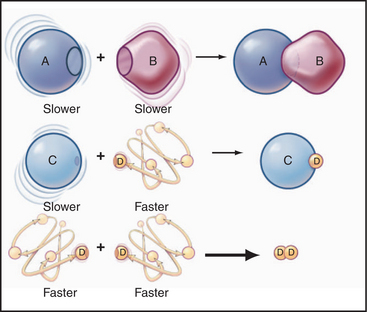
Second-order reactions have two reactants (Fig. 4-2). The general case is

Figure 4-2 second-order reactions. In second-order reactions, two molecules must collide with each other. The rate of these collisions is determined by their concentrations and by a collision rate constant (arrows). The collision rate constant depends on the sum of the diffusion coefficients of the reactants and the size of their interaction sites. The rate of diffusion in a given medium depends on the size and shape of the molecule. Large molecules, such as proteins, move more slowly than small molecules, such as adenosine triphosphate (ATP). A protein with a diffusion coefficient of 10⁻¹¹ m² s⁻¹ diffuses about 10 mm in a second in water, while a small molecule such as ATP diffuses 100 times faster. The rate constants (arrows) are about the same for A + B and C + D because the large diffusion coefficient of D offsets the small size of its interaction site on C. Despite the small interaction size, D + D is faster because both reactants diffuse rapidly.

A common example in biology is a bimolecular association reaction, such as

where A and B are two molecules that bind together. Some examples are binding of substrates to enzymes, binding of ligands to receptors, and binding of proteins to other proteins or nucleic acids.

The rate of a second-order reaction is the product of the concentrations of the two reactants, R₁ and R₂, and the second-order rate constant, k:

The second-order rate constant, k, has units of M⁻¹ s⁻¹ (pronounced “per molar per second”). The units for the reaction rate are

the same as a first-order reaction.

The value of a second-order “association” rate constant, k₊, is determined mainly by the rate at which the molecules collide. This collision rate depends on the rate of diffusion of the molecules (Fig. 4-2), which is determined by the size and shape of the molecule, the viscosity of the medium, and the temperature. These factors are summarized in a parameter called the diffusion coefficient, D, with units of m² s⁻¹. D is a measure of how fast a molecule moves in a given medium. The rate constant for collisions is described by the Debye-Smoluchowski equation, a relationship that depends only on the diffusion coefficients and the area of interaction between the molecules:

where b is the interaction radius of the two particles (in meters), the Ds are the diffusion coefficients of the reactants, and N _o is Avogadro’s number. The factor of 10³ converts the value into units of M⁻¹ s⁻¹.

For particles the size of proteins, D is approximately 10⁻¹¹ m² s⁻¹ and b is approximately 2 × 10⁻⁹ μ, so the rate constants for collisions of two proteins are in the range of 3 × 10⁸ M⁻¹ s⁻¹. For small molecules such as sugars, D is approximately 10⁻⁹ m² s⁻¹ and b is approximately 10⁻⁹ μ, so the rate constants for collisions of a protein and a small molecule are about 20 times larger than collisions of two proteins, in the range of 7 × 10⁹ M⁻¹ s⁻¹. On the other hand, experimentally observed rate constants for the association of proteins are 20 to 1000 times smaller than the collision rate constant, on the order of 10⁶ to 10⁷ M⁻¹ s⁻¹. The difference is attributed to a steric factor that accounts for the fact that macromolecules must be correctly oriented relative to each other to bind together when they collide. Thus, the complementary binding sites are aligned correctly only 0.1% to 5% of the times that the molecules collide.

Many binding reactions between two proteins, between enzymes and substrates, and between proteins and larger molecules (e.g., DNA) are said to be “diffusion limited” in the sense that the rate constant is determined by diffusion-driven collisions between the reactants. Thus, many association rate constants are in the range of 10⁶ to 10⁷ M⁻¹ s⁻¹.

To review, the rate of a second-order reaction is simply the product of a constant that is characteristic of the reaction and the concentrations of the two reactants. In biology, the rates of many bimolecular association reactions are determined by the rates of diffusion-limited collisions between the reactants.

Reversible Reactions

Most reactions are reversible, so the net rate of a reaction is equal to the difference between the forward and reverse reaction rates. The forward and reverse reactions can be any combination of first- or second-order reactions. A reversible conformational change of a protein from A to ^* is an example of a pair of simple first-order reactions:

The forward reaction rate is k₊A with units of M s⁻¹, and the reverse reaction rate is k_–^* with the same units. At equilibrium, when the net concentrations of A and ^* no longer change,

This equilibrium constant is unitless, since the units of concentration and the rate constants cancel out.

The same reasoning with respect to the equilibrium constant applies to a simple bimolecular binding reaction:

where A and B are any molecule (e.g., enzyme, receptor, substrate, cofactor, or drug). The forward (binding) reaction is a second-order reaction, whereas the reverse (dissociation) reaction is first-order. The opposing reactions are

Only gold members can continue reading. Log In or Register to continue

Related

Stay updated, free articles. Join our Telegram channel

Tags: Cell Biology

Jun 18, 2016 | Posted by admin in BIOCHEMISTRY | Comments Off

Full access? Get Clinical Tree

Get Clinical Tree app for offline access

Get Clinical Tree app for offline access