OUTLINE
Liquid-Liquid Aliquots and Serial Dilutions
I. GENERAL PRINCIPLES
A. In pharmacy we often deal with potent drug substances that require accurate measurement when preparing dosage forms for our patients. When the quantity of drug desired requires a degree of precision in measurement that is beyond the capability of the available measuring devices, the pharmacist or pharmacy technician may use the aliquot method of measurement.
B. Aliquot means “contained an exact number of times in something else.”Therefore, 5 is an aliquot part of 15 because 5 is contained exactly 3 times in 15.
C. When aliquots are used in pharmacy, the general procedure is as follows:
1. Weigh or measure an amount of the desired drug that is within the degree of accuracy provided by the measuring device.
2. Weigh or measure a compatible, inert diluent. For solid aliquots, lactose is a common diluent. For liquid aliquots, water is used if possible, but alcohol or another pharmaceutical solvent may also be used when solubility or miscibility dictates this.
3. Add the diluent to the drug with adequate mixing to give a homogeneous mixture or solution. In all cases when combining powders, use geometric dilution and mix thoroughly using trituration in a glass mortar. (Note:A description of geometric dilution is given in Chapter 25, Powders: the Principles of Compounding for Powders section.)
4. Weigh or measure an aliquot part of the mixture that contains exactly the desired amount of drug.
D. How are the numbers for aliquot parts determined?
1. Examples given later show several commonly used methods. Any method is satisfactory as long as the correct amount of drug is obtained. Use a system that makes sense to you because this usually means that there is less potential for error.
2. Because aliquots usually are used for potent drugs, it is always best to have a colleague independently check the amounts calculated.
3. For the examples given next, the following assumptions were made: (i) the available balance has a minimum weighable quantity (MWQ) of 120 mg; (ii) the smallest graduated cylinder available has a capacity of 10 mL with a minimum measurable quantity (MMQ) of 2 mL (20% of the capacity of the graduated cylinder); (iii) the smallest syringe or micropipette available has a MMQ of 0.2 mL; (iv) lactose can be used as the inert diluent for the solid-solid aliquots; and (v) water can be used as the inert diluent for liquid aliquots.
II. SIMPLE SOLID-SOLID ALIQUOTS
A. Aliquot Method 1: MWQ Method
1. This method is the simplest.
a. An amount of drug is weighed that is within the degree of accuracy provided by the balance. For economic reasons, the amount chosen is usually the MWQ.
b. The drug is diluted with an arbitrary amount of diluent using geometric dilution when appropriate.
c. The amount of the dilution that will give the desired amount of drug is calculated, and this amount is weighed.
2. This method is usually the easiest aliquot method to use, especially when the amount of drug being weighed is restricted to a given value, such as the MWQ. This is true when the desired drug is a controlled substance because only minimum waste is allowed for controlled substances. Using the MWQ is also preferred when the drug is expensive.
3. This method is illustrated with several examples. The first example (10.1), Trial 1, starts with the basic necessary steps. Trial 1 is then analyzed, and the method is refined. Example 10.2, Trial 2, shows the results of these modifications. A final analysis is then given to show additional possibilities. The objective of presenting the method in this way is to show a pattern of possible thought processes that can be used in a general sense for developing methods of problem solving when dealing with pharmaceutical calculations.
drug/amount desired: codeine 20 mg
1. Trial 1: Basic steps
a. Weigh the MWQ of codeine: 120 mg.
b. Weigh an arbitrary amount of lactose that is ≥ the MWQ: 300 mg.
c. Mix the two powders thoroughly by triturating in a mortar.
d. Calculate the total weight of the dilution: 120 mg + 300 mg = 420 mg.
e. Calculate the number of milligrams of dilution that contain the desired 20 mg of codeine.
By proportion:

By dimensional analysis:
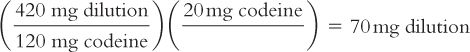
f. Weigh this calculated amount of the dilution, 70 mg, to get the desired 20 mg of codeine.
2. Analysis of Trial 1
Analysis of these calculations reveals that some judgment is required in selecting the quantity of diluent to add to the drug. In this case, the required amount of the aliquot was calculated to be 70 mg, which is below the MWQ. The following are general guidelines for selecting the amount of diluent to use:
a. Pick a quantity of diluent that will give aliquots that are at or above the MWQ. In this case, it is obvious that 300 mg of lactose is not enough diluent when the desired amount of drug is 20 mg. The 70 mg of the dilution, which is the amount needed to give 20 mg of codeine, is below the MWQ of 120 mg and cannot be weighed with the desired level of accuracy.
b. When possible, pick convenient amounts of diluent to make the mathematics easy. It is always best to use simple numbers, or amounts that reduce to simple numbers, because it is then easier to spot errors. In this case, if the amount of diluent is chosen to be a multiple of 120 mg (the amount of codeine weighed), then the fraction “mg codeine/mg dilution” reduces to a simple integer that is easily multiplied times the “mg codeine” to get the desired “mg dilution.” The following example illustrates this principle.
Trial 2: Revised steps
1. This example is a repeat of the foregoing problem using a more “convenient” quantity of diluent that will give an aliquot ≥ the MWQ.
a. Weigh the MWQ of codeine: 120 mg.
b. Weigh a convenient amount of lactose (that is, a multiple of 120 mg) that will give an aliquot ≥ 120 mg, the MWQ: 600 mg is selected.
c. Add the lactose to the codeine using geometric dilution and mix the two powders thoroughly by triturating in a mortar.
d. Calculate the weight of the dilution: 120 mg + 600 mg = 720 mg.
e. Calculate the number of milligrams of dilution that contain the desired 20 mg of codeine.
By proportion:

By dimensional analysis:
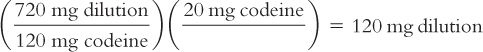
f. Weigh this calculated amount of the dilution to get the desired 20 mg of codeine.
2. Analysis of Trial 2
a. As you can see, 720 is a multiple of 120 (6 × 120 = 720), so the fraction 120/720 reduces to 1/6, and the mathematics becomes a simple matter of multiplying 20 mg of codeine by 6 to get 120 mg of dilution.

Even though most of us use calculators for math operations, it is important to look at the answers we get to see whether they seem reasonable. This sort of inspection is much easier if the numbers are simple.
b. In using this method, you may wonder, What is the best way to pick the quantity of diluent so that the amount of dilution needed is at least the MWQ, but the amounts are not so large as to waste ingredients or give an aliquot that is excessively bulky? There are several ways in which this may be accomplished.
(1) Pick any reasonable amount, do the math and, if the amount of dilution calculated is too little or too much, pick a different amount. While simple, this can be tedious.
(2) In picking amounts, notice that the amount of diluent needed is not completely arbitrary. An inspection of the calculations given here reveals that the smaller the amount of drug needed (20 mg in this case), the larger the amount of diluent needed to give a minimum amount of dilution to weigh.
(3) Further inspection of the equations in Trial 2 reveals that instead of picking the amount of the diluent and solving for the amount of the aliquot, you may also set up the equation by picking the amount of the aliquot and solving for the amount of the dilution. For example, if you want 120 mg for the aliquot, set up the equation as shown here:
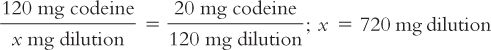
You will need to remember that the 720 mg is the total amount of the dilution (i.e., drug plus diluent). To determine the amount of diluent, subtract the quantity of drug weighed from this total to obtain the amount of the diluent. In this case,
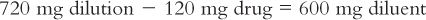
(4) For pharmacists who like formulas, the formula given below may be useful:
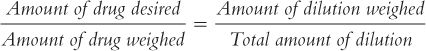
To use this formula, fill in the desired quantities for Amount of drug desired, Amount of drug weighed, and Amount of dilution weighed. Then, solve for Total amount of dilution. In the foregoing example:
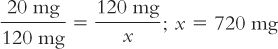
As with the previous example, remember that 720 mg is the total amount of the dilution (i.e., drug plus diluent). To determine the amount of diluent, subtract the quantity of drug weighed from this total to obtain the amount of the diluent. Though formulas may simplify solving pharmaceutical calculations, the problem with using a formula is that you have to remember it—unless, of course, it is intuitive to you.
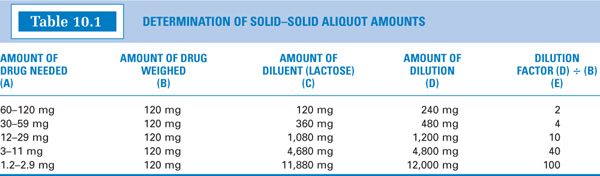
(5) You may wish to perform the calculations for aliquots for a variety of drug weights and construct a table of values such as the one shown in Table 10.1. Using a table of that type is fairly easy.
(a) Determine the amount of drug needed: 20 mg.
(b) Weigh 120 mg of the drug. (Notice in column (B) of Table 10.1 that this amount is always the same. This table was constructed for a Class III torsion balance, and 120 mg was chosen as the amount to weigh because that is the MWQ for that balance; a similar table using 20 mg for a typical electronic balance could also be constructed.)
(c) Determine the weight range for the amount of drug needed from column (A), 12–29 mg, and read off the amount of lactose or other diluent from column (C), 1,080 mg. The combined weight of the drug and diluent is shown in column (D), 1,200 mg.
(d) Calculate the amount of dilution to weigh that will contain the desired amount of drug.

(e) Alternatively, you may read the appropriate dilution factor given in column (E), which in this case is 10, and multiply the dilution factor times the amount of drug needed to get the amount of aliquot to weigh.
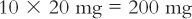
When using this approach, it is always best to check the values obtained by completing a full calculation using the chosen numbers as shown in the calculation in part (d).
B. Aliquot Method 2: Dilution Factor Method

1. This method is useful when there is more flexibility in the amount of drug that may be weighed; for example, you are not required to use the MWQ.
2. This method consists of the following steps:
a. The quantity of drug to be weighed is determined by multiplying the amount of drug needed by an appropriately determined factor, called the dilution factor.
b. An arbitrary amount of diluent is weighed and added.
c.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree