Thermochemistry: The role of heat in chemical and physical changes
Thermochemistry lies at the heart of one of the areas that makes chemistry so important. Energy can be extracted from a chemical system when bonds are rearranged in the making of products from reactants. This energy can be harvested to perform work, to generate steam and electricity, and to provide warmth in our homes. The energy changes that occur during reactions and phase changes are directly dependent on bonding and intermolecular interactions. Thus, the measurement of temperature changes during these processes is a direct measure of the strength of these interactions. By probing the strength of bonds and intermolecular interactions, thermochemical measurements provide tests to our models of these interactions.
10.1 Stoichiometry and extent of reaction
Extent of reaction is given the symbol ξ (Greek xi). A balanced stoichiometric chemical reaction is written with stoichiometric coefficients a, b, and so on, which are all positive numbers

The IUPAC defines stoichiometric numbers νA, νB, and so on, as signed quantities, which are negative for reactants and positive for products. Stoichiometric coefficients are the absolute values of the stoichiometric numbers. In other words, a = |vA| = −vA but z = |vz|vz. The extent of reaction has units of moles and is defined by
This is a positive number that is the same for all reactants and products. ni is the amount of substance (moles) present at a given time, while ni,0 is the amount of substance present initially. The stoichiometric equation must be specified to define the extent of reaction. From Eq. (10.1) the extent of reaction can be used to calculate the amount of substance present at any given time,
By differentiation, it yields the change in the amount of substance
10.2 Standard enthalpy change
The standard enthalpy change, ΔH°, is obtained when the reactants and products of a given reaction are present in their standard states at a specified temperature. The standard state is the pure form in equilibrium at 1 bar. Generally, the temperature – if not specified – is taken to be 298.15 K (25 °C). Most elements in the Periodic Table are solids in their standard state at 298 K. The most stable form of the solid is taken as the standard state. For example, graphite is the standard state of carbon, and not diamond or graphene or carbon nanotubes or amorphous carbon. Several other elements have multiple allotropic forms with the standard states as follows: Sb (metallic), As(gray), P(white), Se(gray), S(rhombic) and Sn(white). You should be familiar with the exceptions. The noble gases are all monatomic gases in their standard states. H2, N2, O2, F2 and Cl2 are all diatomic gases in the standard state. Br2 is a diatomic liquid and I2 is a diatomic solid, but At is an atomic solid. Hg is a monatomic liquid. Ga becomes a liquid just above room temperature at 302.91 K.
Enthalpy changes can be measured for a variety of processes. The process is specified by a subscript after the delta, for example ΔrH for the enthalpy change that occurs during a reaction. The subscript m after the H specifies the value as a molar enthalpy. The m is often dropped in the literature, so always check the units to determine whether the enthalpy change is given as an absolute value in kJ or molar value in kJ mol−1. The subscripts used to denote a number of processes are listed in Table 10.1. Recommended superscripts appear in Table 10.2.
Table 10.1 Recommended subscripted abbreviations to denote processes.
| Absorption | abs |
| Adsorption | a or ads |
| Atomization | at |
| Combustion reaction | c |
| Desorption | des |
| Dilution | dil |
| Displacement | dpl |
| Formation reaction | f |
| Fusion, melting | fus |
| Hydration | hyd |
| Immersion | imm |
| Mixing | mix |
| Phase transition | trs |
| Reaction in general | r |
| Solution | sol |
| Sublimation | sub |
| Transition | trs |
| Triple point | tp |
| Vaporization | vap |
Table 10.2 Recommended superscript designations.
| Activated complex | ‡ |
| Apparent | app |
| Excess quantity | E |
| Ideal | id |
| Infinite dilution | ∞ |
| Pure substance | * |
| Standard | ° |
Reactions are classed as either exothermic or endothermic based on the value of the standard enthalpy change for the reaction, ΔrH°. ΔrH° < 0 defines an exothermic reaction, ΔrH° > 0 defines an endothermic reaction, and ΔrH° = 0 defines a thermoneutral reaction. An increase in temperature tends to favor product formation for endothermic reactions but disfavors products for exothermic reactions.
From the First Law of Thermodynamics and the definition of work at constant pressure for a system in which only pV work is available, the relationship between changes in internal energy and enthalpy is
Therefore, at constant pressure where Δp = 0,
In other words, internal energy changes and enthalpy changes are virtually identical for any process run at atmospheric pressure that does not involve a change in the volume. If gases are not involved in the process, the change in volume is unlikely to be significant. However, under extremes of pressure – for instance in a geochemical setting or in a diamond anvil cell – the p ΔV term may be significant even if only solids are involved.
10.2.1 Example
By what amount will the change in internal energy differ from the change in enthalpy for the reaction of 0.0500 mol of MgCO3 with excess dilute HCl(aq) at standard temperature and pressure (STP) for which p = 1 bar and T = 273 K?
Start with a balanced chemical reaction

Accordingly, 0.05 mol MgCO3 produces 0.05 mol CO2. The production of a gas leads to a volume change, and the work performed by the system is accomplished by expanding this gas against the pressure of the surroundings. Use the ideal gas law to calculate the volume change and then the work. At constant p and T, the work is given by

where Δngas is the change in gas moles = 0.0500 mol.

The work is done by the system on the surroundings and is, therefore, negative. The difference between the internal energy change and the enthalpy change on a molar basis is

10.2.2 Directed practice
Show that for the same reaction at 298 K, the work done by the system is −2.48 kJ mol−1.
10.2.3 Temperature dependence of enthalpy of reaction
In Section 9.6 we have shown that the temperature dependence of the enthalpy is given by
Since Eq. (10.6) is true for each individual substance in the reaction, we can perform the appropriate sums and differences of the enthalpies of all of the reactants and products to calculate ΔrH for the reaction. From this, we can show that the change in enthalpy of reaction with temperature follows Kirchhoff’s law
where
For all reactions over small ranges of temperature, and for some reactions over extended ranges of temperature change, ΔrC°p, m is constant and can be pulled from the integral. The enthalpy of reaction at T2 is then given by
10.3 Calorimetry
The standard method for determining the enthalpy change during a reaction is calorimetry – the measurement of temperature rise after a known amount of material has reacted. The temperature rise is related to the heat evolved in the process, q, and the heat capacity, C, by the fundamental equation of calorimetry,
A calorimeter must correspond as close as possible to a closed system. Neither heat nor matter should be exchanged with the surroundings. This is not that difficult to approximate in practice if the reaction can be run in a thermos flask and there is some way to initiate the reaction so that it is clear what the temperature is before the reaction and after the reaction. Initiation of the reaction may occur after mixing of reagents, which requires some sort of mechanical intervention inside of the thermos flask. This may require dropping one container into another, breaking a barrier between containers, or the injection of fluids.
One of the most common types of calorimeter is a constant volume bomb calorimeter. This is shown in Fig. 10.2. The bomb is a stainless steel tube with a removable cap that can be sealed. A solid or liquid sample is placed in a cup near an igniter. The igniter is a wire through which current is passed to heat it sufficiently to initiate combustion. The igniter is consumed in the reaction. The bomb is sealed after the sample is loaded into the cup and a fresh wire has been coiled to form the igniter. The bomb is pressurized with excess O2 to a pressure of approximate 3 MPa. The bomb is then placed in a known quantity of water inside of a thermos flask. A thermometer is placed in the water, which is stirred vigorously. The water provides good thermal contact with the stainless steel bomb. The mass of the sample used is matched to the mass of the water and the bomb so that the temperature rise that accompanies the reaction is no more than a few degrees, usually about 2–3 K. In principle, the measurement should be made at close to constant temperature so that the temperature dependence of the heat capacities of materials involved need not be considered. On the other hand, if the temperature rise is too small, uncertainties in the measurement are increased. Hence, the temperature rise of ΔT ≈ 2–3 K represents a good compromise.

Figure 10.1 Fire is a manifestation of a complex series of radical-driven chain reactions. From cooking, to boiling water to driving turbines, to propulsion from internal combustion engines, the thermochemistry of combustion has a long and intricate relationship with human culture and its development. Photograph provided by Hope Michelsen at the Combustion Research Facility, Sandia National Laboratories.
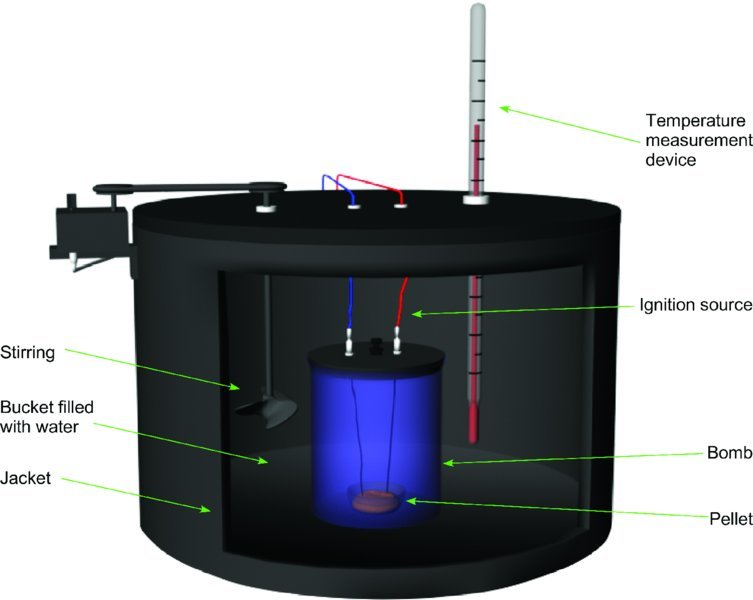
Figure 10.2 Design of a constant volume bomb calorimeter. The sample rests inside the bomb in a cup. Current is passed through a wire to initiate combustion in an excess of O2. The stainless steel bomb is submerged in water inside of an insulated bucket.
The bomb, its contents, and the water-filled thermos with temperature measurement are then placed inside of a thermally isolated jacket. Highly accurate work will correct for the energy provided by mixing and the igniter, as well as accounting for thermal drift. The system is allowed to equilibrate thermally, after which the temperature is recorded for several minutes before the ignition and several minutes after ignition, as shown in Fig. 10.3. Extrapolation is then used to determine the temperature change, ΔT. In many practical applications benzoic acid is used as a standard for calibration.
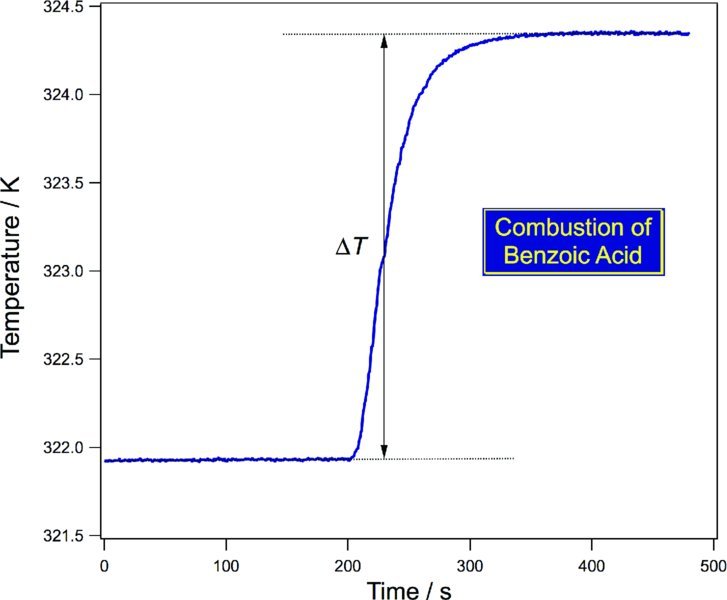
Figure 10.3 Calorimetry data obtained for the combustion of benzoic acid in pure O2(g) with a bomb calorimeter.
10.3.1 Example
A bomb calorimeter is built with a specific heat capacity of 1.58 kJ K−1. Calculate the molar internal energy change if the combustion of 120 mg of naphthalene, C10H8(s), leads to a temperature rise of 3.06 K.
Because of the small temperature change, we treat the heat capacity as constant, pull it from the integral in Eq. (10.10) and arrive at Eq. (10.11),
The heat qV generated by the reaction at constant volume is given by the product of the amount of substance combusted and the internal energy change,
Note how the subscript c is used to denote this internal energy change specifically corresponds to the change during combustion. With a molar mass of 128.17 g mol−1, 120 mg corresponds to 0.936 mmol of naphthalene. By the First Law of Thermodynamics, the heat released by combustion − qV must be equal and opposite to the energy transferred to the calorimeter q,
Equating these expressions for heat evolved by the reaction and heat absorbed by the calorimeter – that is, assuming a perfect calorimeter with no contribution from the igniter – we solve the resulting equation for internal energy change

10.3.2 Example
Calculate ΔcH°m at 298.15 K for the benzoic acid calorimetry experiment in Example 7.9.2.3. Recall that 0.4089 g of C6H5COOH were combusted at Ti = 20.17 °C with Tf = 22.22 °C corresponding to an internal energy change of ΔcU°m = −3226 kJ mol−1.
Start with a balanced reaction

This is written as a standard combustion reaction. A standard combustion reaction corresponds to the reaction of 1 mol of the named reactant with however many moles of gaseous O2 it takes to oxidize it completely to products. The reaction temperature is 298.15 K unless otherwise stated. If the reactant is a hydrocarbon (or contains only H, C and O), the products are CO2(g) and H2O(l). In principle, the same equation applies to a compound containing another element if that element ends in its standard state; for example, N if the product is N2(g). In general, however, the exact products containing the other elements must be known in order to calculate the enthalpy of combustion.
To calculate the value of ΔcH°m, recall that ΔcH = ΔcU + Δ(pV). When all reactants and products are in condensed phases at near atmospheric pressure, Δ(pV) is negligible in comparison with ΔcH and ΔcU. When gases are involved, Δ(pV) cannot be ignored. Assuming ideal gas behavior, we have
Δngas is the change in the amount of substance of gas during the course of one full stoichiometric equivalent of reaction. In other words, Δngas is the difference between the stoichiometric numbers of the gaseous products minus the stoichiometric numbers of the gaseous reactants, Δngas = νgas,products – νgas,reactants. T refers to the final temperature. For the reaction as written above Δngas = 7 – 7.5 = −0.5. Hence

and the enthalpy of combustion is ΔcH°m = −3227 kJ mol−1 at the final temperature of 293.32 K. To correct this value to the reference temperature of 298.15 K, we apply Eq. (10.9)

with T2 = 298.15 K, T1 = 293.32 K, ΔT = T2 − T1 and

The temperature correction amounts to only −33 J mol−1 and is inconsequential in this case. What does the mol−1 refer to? It refers to one full stoichiometric equivalent of reaction as written. Energy in the amount of 3227 kJ is evolved per mole of C6H5COOH combusted but per 7.5 mol of O2 consumed. In other words, per mole for the balanced reaction as written. The enthalpies of combustion of several compounds are listed in Table 10.3.
Table 10.3 Standard enthalpy of combustion ΔcH°m and specific heat of combustion at 298.15 K for several compounds. Values taken from the 96th edition of the CRC Handbook of Chemistry and Physics.
| Compound | Formula | M / g mol−1 | ΔcH°m / kJ mol−1 | Specific heat of combustion / kJ g−1 |
|---|---|---|---|---|
| Graphite | C | 12.011 | 393.5 | 32.76 |
| Hydrogen | H2 | 2.0159 | 285.8 | 141.77 |
| Ammonia | NH3 | 17.031 | 382.8 | 22.48 |
| Methane | CH4 | 16.043 | 890.8 | 55.53 |
| Propane | C3H8 | 44.096 | 2219.3 | 50.33 |
| Octane | C8H18 | 114.229 | 5470 | 47.89 |
| Naphthalene | C10H8 | 128.171 | 5156.3 | 40.23 |
| Biphenyl | C12H10 | 154.207 | 6251 | 40.54 |
| Methanol | CH4O | 32.042 | 726 | 22.66 |
| Ethanol | C2H6O | 46.068 | 1366.8 | 29.67 |
| 1-Naphthol | C10H8O | 144.17 | 4957 | 34.38 |
| Benzophenone | C13H10O | 182.217 | 6510 | 35.73 |
| Benzoic acid | C7H6O2 | 122.122 | 3228.2 | 26.43 |
| Glucose | C6H12O6 | 180.155 | 2803 | 15.56 |
| Lactose | C12H22O11 | 342.296 | 5630 | 16.45 |
10.3.3 Directed practice
Why is the determination of the standard molar enthalpy of combustion typically performed with a few grams of material rather than a mole?
10.4 Phase transitions
When heat is added to a substance, its temperature increases in accord with Eq. (10.11). This is shown in Fig. 10.4. As long as no phase transitions or reactions occur, the temperature increases in a simple manner determined by the heat transfer rate and the heat capacity. At a phase transition temperature, further addition of heat does not increase the temperature. Instead, the system enters an isothermal region in which the added heat is used to facilitate the phase transition rather than increasing the temperature. Once all of the substance has been converted to the new phase, further heat transfer leads to increases in temperature again. The new phase will have a different heat capacity.

Figure 10.4 Heating of a liquid, water in this example, with heat transfer at a constant rate leads to an increase in the temperature of the liquid to the boiling point. Once a phase transition temperature is reached, the temperature does not increase. The added heat is used to overcome the enthalpy of the transition (vaporization in this case). After all of the liquid has vaporized, added heat increases the temperature of the gas. The gas has a smaller heat capacity than the liquid; therefore, the slope of the heating gas curve is greater than the slope of the heating liquid curve. Slight deviations from linearity in the heating curves result from changes in the heat capacities with temperature.
The example of water is shown in Fig. 10.4. starting in the liquid phase. The liquid generally has the highest heat capacity of any phase of a material so the response of temperature to heat transfer is the smallest for this phase – that is, the slope of the temperature versus time curve is the shallowest. However, upon heating, the pattern of increasing temperature, followed by an isothermal region, followed by further increasing temperature is the same for any first-order phase transition. For first-order phase transitions (the most common kind, as discussed and defined further in Chapter 13) there is always a discontinuous change in the heat capacity from one phase to the next. There also will always be an isothermal region because such phase transitions are accompanied by an enthalpy of transition that has to be supplied to make the transition occur (or removed upon cooling).
Phase changes are accompanied by changes in the orientations and distances between molecules (or atoms). The existence of intermolecular interactions means that phase changes will also be accompanied by enthalpy changes. The more drastic the change in molecular orientations and intermolecular distance, the larger the enthalpy changes. The melting of water is endothermic by 6.01 kJ mol−1 at 273 K, whereas vaporization of water at 298 K is endothermic by 43.98 kJ mol−1. The vaporization of Au is endothermic by 324 kJ mol−1. Therefore, both the strength of intermolecular interactions and the extent of change of relation of molecules to one another in the two phases determine the magnitude of the enthalpy change during the phase transition.
The enthalpy change for a phase transition is denoted ΔtrsH. The heat evolved at constant pressure is equal to the enthalpy change. The standard temperature of a phase transition is the temperature at which the phase transition occurs at equilibrium when the pressure is equal to the standard state value of p° = 1 bar. In condensed phases it is of little consequence whether the standard state pressure is taken as 1 bar or 1 atm. The difference is more measureable for gases. Therefore, one will encounter the terms normal transition temperature (corresponding to p = 1 atm) in addition to the standard transition temperature (p = 1 bar).
The heat evolved at the standard pressure while a phase transition occurs at its standard transition temperature is equal to the standard enthalpy of the phase transition. In molar units this is
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


















