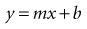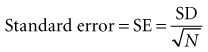This equation is the formula for a straight line in analytic geometry. It is also the formula for simple regression analysis in statistics, although the letters used and their order customarily are different.

In the mathematical formula the b is a constant and stands for the y-intercept (i.e., value of y when the variable x equals 0). The value m also is a constant and stands for the slope (amount of change in y for a unit increase in the value of x). The important point is that in mathematics, one of the variables (x or y) is unknown and needs to be calculated, whereas the formula and the constants are known. In statistics the reverse is true. The variables x and y are known for all persons in the sample, and the investigator may want to determine the linear relationship between them. This is done by estimating the slope and the intercept, which can be done using the form of statistical analysis called linear regression (see Chapter 11).

As a general rule, what is known in statistics is unknown in mathematics, and vice versa. In statistics the investigator starts from specific observations (data) to induce (estimate) the general relationships between variables.

II Process of Testing Hypotheses

Hypotheses are predictions about what the examination of appropriately collected data will show. This discussion introduces the basic concepts underlying common tests of statistical significance, such as t-tests. These tests determine the probability that an observed difference between means, for example, represents a true, statistically significant difference (i.e., a difference probably not caused by chance). They do this by determining if the observed difference is convincingly different from what was expected from the model. In basic statistics the model is usually a null hypothesis that there will be no difference between the means.

The discussion in this section focuses on the justification for, and interpretation of, the p value, which is the probability that a difference as large as one observed might have occurred by chance. The p value is obtained from calculating one of the standard statistical tests. It is designed to minimize the likelihood of making a false-positive conclusion. False-negative conclusions are discussed more fully in Chapter 12 in the section on sample size.

A False-Positive and False-Negative Errors

Science is based on the following set of principles:

Previous experience serves as the basis for developing hypotheses.

Hypotheses serve as the basis for developing predictions.

Predictions must be subjected to experimental or observational testing.

If the predictions are consistent with the data, they are retained, but if they are inconsistent with the data, they are rejected or modified.

When deciding whether data are consistent or inconsistent with the hypotheses, investigators are subject to two types of error. An investigator could assert that the data support a hypothesis, when in fact the hypothesis is false; this would be a false-positive error, also called an alpha error or a type I error. Conversely, they could assert that the data do not support the hypothesis, when in fact the hypothesis is true; this would be a false-negative error, also called a beta error or a type II error.

Based on the knowledge that scientists become attached to their own hypotheses, and the conviction that the proof in science (as in courts of law) must be “beyond a reasonable doubt,” investigators historically have been particularly careful to avoid false-positive error. This is probably best for theoretical science in general. It also makes sense for hypothesis testing related specifically to medical practice, where the greatest imperative is “first, do no harm” (Latin primum non nocere). Although it often fails in practice to avoid harm, medicine is dedicated to this principle, and the high standards for the avoidance of type I error reflect this. However, medicine is subject to the harms of error in either direction. False-negative error in a diagnostic test may mean missing a disease until it is too late to institute therapy, and false-negative error in the study of a medical intervention may mean overlooking an effective treatment. Therefore, investigators cannot feel comfortable about false-negative errors in either case.

Box 10-1 shows the usual sequence of statistical testing of hypotheses; analyzing data using these five basic steps is discussed next.

Box 10-1 Process of Testing a Null Hypothesis for Statistical Significance

1. Develop the null and alternative hypotheses.

2. Establish an appropriate alpha level.

3. Perform a suitable test of statistical significance on appropriately collected data.

4. Compare the p value from the test with the alpha level.

5. Reject or fail to reject the null hypothesis.

1 Develop Null Hypothesis and Alternative Hypothesis

The first step consists of stating the null hypothesis and the alternative hypothesis. The null hypothesis states that there is no real (true) difference between the means (or proportions) of the groups being compared (or that there is no real association between two continuous variables). For example, the null hypothesis for the data presented in Table 9-2 is that, based on the observed data, there is no true difference between the percentage of men and the percentage of women who had previously had their serum cholesterol levels checked.

It may seem strange to begin the process by asserting that something is not true, but it is much easier to disprove an assertion than to prove that something is true. If the data are not consistent with a hypothesis, the hypothesis should be rejected and the alternative hypothesis accepted instead. Because the null hypothesis stated there was no difference between means, and that was rejected, the alternative hypothesis states that there must be a true difference between the groups being compared. (If the data are consistent with a hypothesis, this still does not prove the hypothesis, because other hypotheses may fit the data equally well or better.)

Consider a hypothetical clinical trial of a drug designed to reduce high blood pressure among patients with essential hypertension (hypertension occurring without an organic cause yet known, such as hyperthyroidism or renal artery stenosis). One group of patients would receive the experimental drug, and the other group (the control group) would receive a placebo. The null hypothesis might be that, after the intervention, the average change in blood pressure in the treatment group will not differ from the average change in blood pressure in the control group. If a test of significance (e.g., t-test on average change in systolic blood pressure) forces rejection of the null hypothesis, the alternative hypothesis—that there was a true difference in the average change in blood pressure between the two groups—would be accepted. As discussed later, there is a statistical distinction between hypothesizing that a drug will or will not change blood pressure, versus hypothesizing whether a drug will or will not lower blood pressure. The former does not specify a directional inclination a priori (before the fact) and suggests a “two-tailed” hypothesis test. The latter does suggest a directional inclination and suggests a “one-tailed” test.

2 Establish Alpha Level

Second, before doing any calculations to test the null hypothesis, the investigator must establish a criterion called the alpha level, which is the highest risk of making a false-positive error that the investigator is willing to accept. By custom, the level of alpha is usually set at p = 0.05. This says that the investigator is willing to run a 5% risk (but no more) of being in error when rejecting the null hypothesis and asserting that the treatment and control groups truly differ. In choosing an arbitrary alpha level, the investigator inserts value judgment into the process. Because that is done before the data are collected, however, it avoids the post hoc (after the fact) bias of adjusting the alpha level to make the data show statistical significance after the investigator has looked at the data.

An everyday analogy may help to simplify the logic of the alpha level and the process of significance testing. Suppose that a couple were given instructions to buy a silver bracelet for a friend during a trip, if one could be bought for $50 or less. Any more would be too high a price to pay. Alpha is similar to the price limit in the analogy. When alpha has been set (e.g., at p ≤0.05, analogous to ≤$50 in the illustration), an investigator would buy the alternative hypothesis of a true difference if, but only if, the cost (in terms of the probability of being wrong in rejecting the null hypothesis) were no greater than 1 in 20 (0.05). The alpha is analogous to the amount an investigator is willing to pay, in terms of the risk of being wrong, if he or she rejects the null hypothesis and accepts the alternative hypothesis.

3 Perform Test of Statistical Significance

When the alpha level is established, the next step is to obtain the p value for the data. To do this, the investigator must perform a suitable statistical test of significance on appropriately collected data, such as data obtained from a randomized controlled trial (RCT). This chapter and Chapter 11 focus on some suitable tests. The p value obtained by a statistical test (e.g., t-test, described later) gives the probability of obtaining the observed result by chance rather than as a result of a true effect. When the probability of an outcome being caused by chance is sufficiently remote, the null hypothesis is rejected. The p value states specifically just how remote that probability is.

Usually, if the observed p value in a study is ≤0.05, members of the scientific community who read about an investigation accept the difference as being real. Although setting alpha at ≤0.05 is arbitrary, this level has become so customary that it is wise to provide explanations for choosing another alpha level or for choosing not to perform tests of significance at all, which may be the best approach in some descriptive studies. Similarly, two-tailed tests of hypothesis, which require a more extreme result to reject the null hypothesis than do one-tailed tests, are the norm; a one-tailed test should be well justified. When the directional effect of a given intervention (e.g., it can be neutral or beneficial, but is certain not to be harmful) is known with confidence, a one-tailed test can be justified (see later discussion).

4 Compare p Value Obtained with Alpha

After the p value is obtained, it is compared with the alpha level previously chosen.

5 Reject or Fail to Reject Null Hypothesis

If the p value is found to be greater than the alpha level, the investigator fails to reject the null hypothesis. Failing to reject the null hypothesis is not the same as accepting the null hypothesis as true. Rather, it is similar to a jury’s finding that the evidence did not prove guilt (or in the example here, did not prove the difference) beyond a reasonable doubt. In the United States a court trial is not designed to prove innocence. The defendant’s innocence is assumed and must be disproved beyond a reasonable doubt. Similarly, in statistics, a lack of difference is assumed, and it is up to the statistical analysis to show that the null hypothesis is unlikely to be true. The rationale for using this approach in medical research is similar to the rationale in the courts. Although the courts are able to convict the guilty, the goal of exonerating the innocent is an even higher priority. In medicine, confirming the benefit of a new treatment is important, but avoiding the use of ineffective therapies is an even higher priority (first, do no harm).

If the p value is found to be less than or equal to the alpha level, the next step is to reject the null hypothesis and to accept the alternative hypothesis, that is, the hypothesis that there is in fact a real difference or association. Although it may seem awkward, this process is now standard in medical science and has yielded considerable scientific benefits.

B Variation in Individual Observations and in Multiple Samples

Most tests of significance relate to a difference between two means or proportions of a variable (e.g., a decrease in blood pressure). The two groups are often a treatment group and a control group. They help investigators decide whether an observed difference is real, which in statistical terms is defined as whether the difference is greater than would be expected by chance alone. In the example of the experimental drug to reduce blood pressure in hypertensive patients, the experimenters would measure the blood pressures of the study participants under experimental conditions before and after the new drug or placebo is given. They would determine the average change seen in the treatment group and the average change seen in the control group and pursue tests to determine whether the difference was large enough to be unlikely to have occurred by chance alone. The fundamental process in this particular test of significance would be to see if the mean blood pressure changes in the two study groups were different from each other.

Why not just inspect the means to see if they were different? This is inadequate because it is unknown whether the observed difference was unusual or whether a difference that large might have been found frequently if the experiment were repeated. Although the investigators examine the findings in particular patients, their real interest is in determining whether the findings of the study could be generalized to other, similar hypertensive patients. To generalize beyond the participants in the single study, the investigators must know the extent to which the differences discovered in the study are reliable. The estimate of reliability is given by the standard error, which is not the same as the standard deviation discussed in Chapter 9.

1 Standard Deviation and Standard Error

Chapter 9 focused on individual observations and the extent to which they differed from the mean. One assertion was that a normal (gaussian) distribution could be completely described by its mean and standard deviation. Figure 9-6 showed that, for a truly normal distribution, 68% of observations fall within the range described as the mean ± 1 standard deviation, 95.4% fall within the range of the mean ± 2 standard deviations, and 95% fall within the range of the mean ± 1.96 standard deviations. This information is useful in describing individual observations (raw data), but it is not directly useful when comparing means or proportions.

Because most research is done on samples, rather than on complete populations, we need to have some idea of how close the mean of our study sample is likely to come to the real-world mean (i.e., mean in underlying population from whom the sample came). If we took 100 samples (such as might be done in multicenter trials), the means in our samples would differ from each other, but they would cluster around the true mean. We could plot the sample means just as we could plot individual observations, and if we did so, these means would show their own distribution. This distribution of means is also a normal (gaussian) distribution, with its own mean and standard deviation. The standard deviation of the distribution of means is called something different, the standard error, because it helps us to estimate the probable error of our sample mean’s estimate of the true population mean. The standard error is an unbiased estimate of the standard error in the entire population from whom the sample was taken. (Technically, the variance is an unbiased estimator of the population variance, and the standard deviation, although not quite unbiased, is close enough to being unbiased that it works well.)

The standard error is a parameter that enables the investigator to do two things that are central to the function of statistics. One is to estimate the probable amount of error around a quantitative assertion (called “confidence limits”). The other is to perform tests of statistical significance. If the standard deviation and sample size of one research sample are known, the standard error can be estimated.

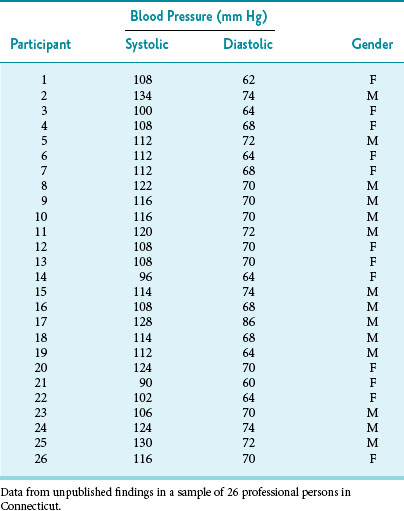
The data shown in Table 10-1 can be used to explore the concept of standard error. The table lists the systolic and diastolic blood pressures of 26 young, healthy, adult subjects. To determine the range of expected variation in the estimate of the mean blood pressure obtained from the 26 subjects, the investigator would need an unbiased estimate of the variation in the underlying population. How can this be done with only one small sample?

Table 10-1 Systolic and Diastolic Blood Pressure Values of 26 Young, Healthy, Adult Participants