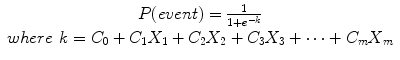We are interested in predicting risk of a disease for an individual because treatment decisions are often based on risk. We will use cardiovascular risk as an example in the following sections since risk prediction is most developed for this disease. Treatment guidelines for high blood pressure or high cholesterol from the American Heart Association differ for people at high risk of cardiovascular disease from those at lower risk. For example, anticoagulant drugs are recommended to people who have atrial fibrillation (a type of heart arrhythmia) if they are at high risk of stroke as determined by their age, whether they have diabetes, a history of stroke, heart failure, and hypertension. Since anticoagulants pose a risk of bleeding, they are not recommended for people who have a low risk of stroke. Prediction of risk is also very useful for public health matters. Knowing what percentage of a population is at high risk can help health planners to mount preventive measures and to plan utilization of resources.

Traditionally accepted risk factors for stroke generally available to clinicians are age, systolic blood pressure, diabetes mellitus, cigarette smoking, prior cardiovascular disease, atrial fibrillation, left ventricular hypertrophy by electrocardiogram, and the use of antihypertensive medication. Equations estimating risk for stroke were developed from prospective studies like the Framingham Study (see Section 4.​10) in which a specified population in the town of Framingham Massachusetts had measures of these variables and were followed up over time to see who developed events like stroke or heart attack and how well the baseline variables studied could predict who would develop the event or outcome.^39–41 With the advent of more sophisticated techniques of measuring certain proteins in the blood (biomarkers), people became interested in refining risk prediction models and in seeing whether certain biomarkers could improve prediction. The question is how do we evaluate whether or how much the new biomarker improves risk prediction? It is an important question because if the biomarker does help in prediction, it may become routinely used in doctors’ offices. Adding biomarkers to risk prediction may indicate that some people, previously thought to be at low risk, are at higher risk and should be treated. On the other hand, this may add to health-care costs, so if it does not improve prediction and has no bearing on treatment decisions, it may not be worth doing the test routinely.

The first indication that a biomarker may be useful is that it is significantly associated with the outcome of interest, either in a logistic regression or a Cox proportional hazards regression model (see Section 4.​19 for explanation of Cox proportional hazards models). The important point to note is that a biomarker may be significantly associated with a disease outcome but that doesn’t mean it necessarily improves risk prediction or reclassifies people into different categories of risk.

As an example, let us consider a protein called CRP (C-reactive protein), which is a marker of general inflammation and can be assayed from a simple blood test. We want to see if it adds to the prediction of stroke.

The ideal situation would be if we measured the biomarker of interest in everyone before the event and then followed them forward in time as some developed the outcome and others did not (in other words, a prospective study) and then added the biomarker to the variables in our risk prediction model. But it gets very expensive to do that, so the usual approach is to do a case–control study and measure the biomarker only in the cases and their controls. This chapter discusses the measures we use to evaluate the additive value of a biomarker in predicting risk.

We will consider risk prediction of ischemic stroke as our example, using data from a case–control study of ischemic stroke nested within the prospective Women’s Health Initiative Observational Study of postmenopausal women.42 We consider the biomarker CRP (C-reactive protein), a marker of inflammation. There were 868 cases and 883 controls who had CRP assayed at the baseline examination and who had had no history of prior stroke. (Actually, the 883 stroke cases were matched to 883 controls on several variables, but 15 of the cases did not have an adequate blood sample, leaving 868 cases and the 883 controls).

First we need to develop a risk prediction equation from our data and then we need to estimate the probability of stroke during a specified period of time for each person in our study population using the risk prediction equation without the biomarker in it. This probability will depend on the specific values for each person of the variables we use in the prediction model. The general idea is that first we have to classify people into risk categories based on our old model without CRP. Next we classify the same people based on our new model, which consists of the variables in the old model plus the biomarker CRP. We compare the two classification schemes with the actual outcomes and see which model predicts more accurately. The sections below describe several measures used to evaluate how well the biomarker adds to prediction. Some excellent papers by Pencina go into further detail.43 ^– 45

We first run a logistic regression model from which we can calculate the probability of stroke. We use variables traditionally used in the prediction of stroke in the Framingham Study: age, systolic blood pressure, diabetes mellitus, cigarette smoking, prior cardiovascular disease, atrial fibrillation, left ventricular hypertrophy by electrocardiogram, and the use of antihypertensive medication in an equation to predict the future occurrence of stroke. (In our example we left out LVH because we did not have data on that and because the prevalence of LVH in the WHI population was very low. Furthermore, the use of antihypertensive medication is a variable that depends on the level of blood pressure, but for simplification we just consider medication = 1 if the woman uses it and = 0 if she does not).

Recall from Chapter 4 that in a logistic regression, the probability of an event is

The parameters in k (the values of C₀ to C_m) are obtained from the logistic regression which can be run in various computer statistical packages like SAS or STATA. In our stroke case–control study, the unconditional logistic regression we calculated with the variables used in the Framingham risk score, k, was

k = (−2.4421 − .0108 (age) + .0207(SBP) + .0003 (on blood pressure medication) + .2228 (history of CHD) + .9868 (current smoker) + .5829 (atrial fibrillation) + .7867 (diabetes) + .2411 (Caucasian))

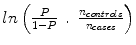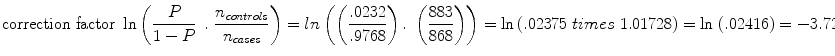
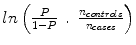But we must make an adjustment to k to account for the fact that it is a case–control study. Thus, we add the term to the intercept of the unconditional logistic regression model; P is the probability of stroke in the target population. In a prospective study we can get P directly because it will just be the number of stroke cases over our follow-up time period (we are choosing 8 years). But because this is a case–control study and P by definition is 50 %, i.e., there are 50 % stroke cases and 50 % controls in our design, we have to estimate P for the target population. For WHI we estimate P as the annual incidence of stroke in the WHI Observational Study which was .0029 annually, times the average follow-up of 8 years or .0232. Thus, our correction factor is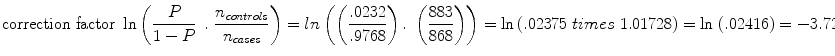

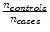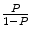
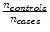Note if there is an equal number of cases and controls, then becomes 1 and the correction factor is simply the natural log of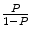

Our corrected k _corrected  = k + correction factor

Next we calculate the probability of stroke within 8 years for each person in our study, using that person’s values of the variables. So, for example, for the i _th person who is a white, nonsmoking woman of age 55, with systolic blood pressure of 120, who does not have diabetes, is not on antihypertensive medication, with no atrial fibrillation or history of heart disease, the probability of stroke in 8 years is calculated as follows:

k _corrected = (−2.4421 − .0108 (55_age) + .0207(120_sbp) + .0003 (0_medications) + .2228 (0_chd) + .9868 (0_{current smoker}) + .5829 (0_{atrial fibrillation}) + .7867 (0_diabetes) + .2411 (1_Caucasian) + (−3.7230_{correction factor}) = −4.0340

and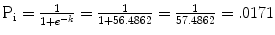

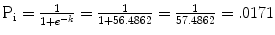
So that person has an estimated risk of stroke in 8 years of 1.7 %.

We calculate these probabilities for each of the stroke cases and each of the controls. Next we divide these probabilities into risk categories. We have chosen the following risk categories: <2 %, 2 % to <5 %, 5 % to <8 %, and ≥8 %. The usually accepted categories are <5 % low risk, 5 to less than 10 % low intermediate risk, 10–20 % high intermediate risk, and >20 % high risk. But in our example, we have a generally low to intermediate risk population (by virtue of the fact that we excluded all those with a previous stroke or heart attack). The risk categories we chose roughly correspond to low, intermediate, and high risk levels used in decisions to initiate treatment to prevent stroke in persons with atrial fibrillation. The person in our example above is in the lowest risk category of <2 %.