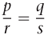2
Rational numbers
Most students will already have at least a basic knowledge of arithmetic and algebra, so the aim of this chapter is to provide a reinforcement of the particular mathematical concepts that are necessary in order to carry out the calculations required in pharmacy. School mathematics courses tend to treat the basic tools of fractions, decimals and percentages as quite separate topics. In this book an attempt is made to provide a more unified and hopefully a more interesting approach.
Proportional sets of numbers
Consider the following sets of data:
A drug is in solution at a concentration of 75 mg to 5 mL:
| weight of drug (mg) | 15 | 30 | 45 | 60 | 75 | 90… |
| volume of solution (mL) | 1 | 2 | 3 | 4 | 5 | 6… |
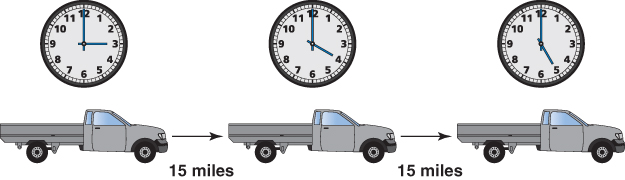
A heavy vehicle travels at a steady speed of 15 miles per hour:
| distance travelled (miles) | 15 | 30 | 45 | 60 | 75 | 90… |
| time taken (hours) | 1 | 2 | 3 | 4 | 5 | 6… |
In these two sets of data we see that the numbers are the same. The same arrangement of numbers serves as an image for two quite different practical situations.
Let us extract the two sets of numbers:
| set A | 15 | 30 | 45 | 60 | 75 | 90… |
| set B | 1 | 2 | 3 | 4 | 5 | 6… |
We see that there is a relationship between the two sets: each number in set A is 15 times the corresponding number in set B.
When one set of numbers is obtained by multiplying each number of the other set by a fixed number, the two sets are said to be proportional. Thus we can say that set A is proportional to set B.
Now consider the next two sets of numbers:
| 3 | 5 | 9… |
| 12 | 20 | 36… |
In this example each lower number is obtained by multiplying the corresponding upper number by 4. Again the two sets are proportional.
Now consider the next two sets of numbers:
| 3 | 8 | 13 | 18… |
| 1 | 2 | 3 | 4… |
There is no fixed number by which the lower set of values can be multiplied in order to arrive at corresponding values of the upper set or vice versa. The two sets are not proportional to each other.
Ratios
Proportional sets can be used to explain the term ‘ratio’.
For the proportional sets:
| 9 | 21 | 30 | 36… |
| 3 | 7 | 10 | 12… |
each number in the upper set is three times the corresponding number in the lower set. Each of the corresponding pairs of numbers is said to be in the ratio three to one.
For the next pair of proportional sets:
| 2 | 5 | 7… |
| 10 | 25 | 35… |
one to five is the ratio of the corresponding pairs. The ratio one to five can also be expressed as 1: 5.
Numbers that represent ratios are called rational numbers. Fractions, decimals and percentages are three kinds of numerals that can be used to represent rational numbers. We will examine the relationships between these three different notations.
Fractions
The ratio 4 to 1 is represented by the fraction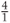 
, which is equivalent to the natural number 4. (The natural numbers are the counting numbers 1, 2, 3…)
The ratio 1 to 5 is represented by the fraction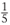 
. The number on top of a fraction is called the numerator and the bottom number is the denominator:
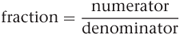
Consider the proportional sets:
| 1 | 2 | 3 | 4… |
| 5 | 10 | 15 | 20… |
We can see that ratio 1 to 5 = ratio 2 to 10 = ratio 3 to 15 and so on. As each ratio can be represented by a fraction, we can write down as many different names as we wish for any given fraction:
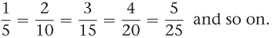
To obtain other names for a given fraction we multiply (or divide) both numerator and denominator by the same number.
Fractions expressed in their lowest terms
As there are many names for the same fraction, the one we tend to use to represent the fraction is the one for which there is no whole number that will divide exactly into both the numerator and the denominator. The fraction is then said to be expressed in its lowest terms.
Multiplication of a fraction by a whole number
We have seen that, if both the numerator and the denominator of a fraction are multiplied by the same number, the resulting fraction is equal to the first one and is just another name for it. To multiply a fraction by a whole number (an integer) we multiply only the numerator by the integer. Thus:
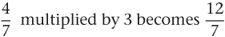
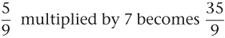
When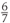 
is multiplied by 8 the result is 
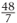, which can be written as 
.
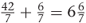Decimals
In the number 127, the 1 represents one hundred, the 2 represents two tens and the 7 represents seven units. The value of each digit is therefore dependent on its position in the number. This system of ‘place values’ is extended for the representation of decimals by introducing a decimal point after the unit value.
| Units | . | Tenths | Hundredths | Thousandths | Ten-thousandths |
| 0 | . | 2 | 3 | ||
| 0 | . | 5 | 2 | 7 |
The number 0.23 is a rational number. The 2 is in the tenths column and the 3 is in the hundredths column. Two tenths and three hundredths make twenty-three hundredths, so 0.23 is another name for the fraction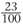 
.
The number 0.527 has a 7 in the thousandths column so it is another name for the fraction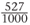 
.
For the reverse process, i.e. to express a fraction in decimal form, the numerator is simply divided by the denominator:
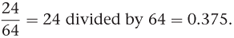
Note that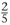 
, 
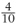and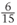 
are different names for the same fraction. Changing each fraction to a decimal:
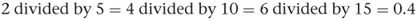
Thus one decimal may be represented by many fractions.
Percentages
5 per cent means 5 per hundred, so 5% represents the same rational number as the fraction
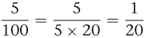
Similarly, 31% is the same as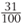 
.
To change a fraction to a percentage, we can change the fraction to a decimal and then examine the decimal to see how many units there are in the hundredths column. The number of hundredths gives the percentage. For example, let us convert the fraction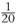 
to a percentage. First divide 1 by 20 to get the decimal 0.05. There is a 5 in the hundredths column. Five hundredths is equal to 5%.
Similarly, the fraction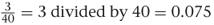 
. There is a 7 in the hundredths column, so there are 7.5 hundredths, which is 7.5%.
Finding a missing value from two proportional sets
Most of the calculations encountered in dispensing are dependent on being able to find missing values from sets of proportional numbers and we are now almost ready to tackle the method for doing this. We have looked at the different forms of rational numbers such as fractions, decimals and percentages that may be required in carrying out the tasks.
We need one more piece of work before we can proceed. Consider the following two proportional sets:
| set A | p | q |
| set B | r | s |
Let us take the sets formed by the values in the vertical columns and call them set C and set D. Thus we have:
| set C | p | r |
| set D | q | s |
As set A is proportional to set B, then we see that the ratio of p to r is equal to the ratio of q to s and this can be expressed as:
