The empirical way is also the basis for the old diagnostic dictum that if you hear hoof beats, it’s more likely to be coming from a horse than from a zebra; horses are more common here than zebras.3 Analogously, it’s more likely (or probable) that the patient has a more common disease than a rare one.
The Theoretical Way
When we’ve gotten tired of losing our money on the nags and want to lose it some other way, we can always shoot craps at Las Vegas or Atlantic City. If you’ve ever been there, you’ll have noticed that the craps tables are covered with a green baize cloth, stating the pay-offs for various throws.4 The odds given for rolling a 7 or 11 on the first throw, or hitting a certain number, are not based on the experience of the croupier; they’re figured out based on the theory of probability. To take a simple example, let’s roll a die. Each of the six sides has an equal likelihood of ending up on top, and which one actually appears is a purely random event. Consequently, the probability of rolling a 3 on this one toss of the die is one in six, or .1667; we don’t have to do this experiment 1,000 times to find this out. We can get even fancier and calculate the probability of getting a 10 with one roll of two dice, of drawing an inside straight, or of rolling a 3 at roulette.5,6
All of these calculations are based on our knowledge of the likelihood of occurrence of various chance events, which is the essence of probability theory, and that’s what we’ll be concerning ourselves with in this chapter. We want to emphasize that all of this is to make you better clinical researchers, not to lead you down the road of corruption by making you better gamblers.
MUTUALLY EXCLUSIVE AND CONDITIONALLY DEPENDENT EVENTS
To understand probability theory, it is necessary to differentiate between two types of events: those that are mutually exclusive and those that are conditionally dependent.
Two events, X and Y, are mutually exclusive if the occurrence of one precludes the occurrence of the other.
The simplest example of this is flipping a coin; heads and tails are mutually exclusive in that, if the head side appears, the tail side won’t, and vice versa. Which party a person votes for in an election for a specific office is a mutually exclusive event.7 However, how a person voted in the last election for all candidates may not be mutually exclusive; the voter may have voted for one party for some offices and for another party for other offices.
Closer to home, respiratory acidosis and alkalosis are mutually exclusive events; if you have one, you can’t simultaneously have the other. On the other hand, cardiac disease and esophageal reflux are not mutually exclusive. If a person has some chest pain, and the ECG confirms the presence of an infarct, it doesn’t necessarily mean that the person can’t have reflux at the same time.
Two events, X and Y, are conditionally dependent if the outcome of Y depends on X, or X depends on Y.
Returning to the gaming tables, the probability of throwing a 5 with a single toss of two dice is 11.11%—there are 36 possible combinations, four of which yield a 5 (1 and 4, 2 and 3, 3 and 2, and 4 and 1). However, if we throw the dice one after the other, and the first die comes up a 1, then the probability that the sum will be 5 is one in six, or 16.67%. That is, the probability of a 5, conditional on the first die being a 1, is .1667. Using the example in Table 5–1, our overall, or unconditional, success rate was 30 out of 50, or 60%. However, our hit rate with Bodies was 30%; that is, our success (Y), conditional on the person having being chosen for his or her body (X), was .30, or 30%.
Turning to more mundane examples, we’ve all heard that the life expectancy of a person is somewhere around 74 years. But this doesn’t tell the whole story. Women live longer than men; 78.1 years for white females born in 1980 as opposed to 70.7 years for white males born in the same year. Black people’s life expectancies are about 7 years less than this, and all the figures are about 3 years more than for people born in 1970. So the probability of a person living to be 80 is conditional on several factors, such as gender, race, and year of birth.
The difference between mutually exclusive and conditionally dependent events is important because we have to figure out probabilities differently for each of them.
Mutually Exclusive Events and the Additive Rule
To illustrate the difference between mutually exclusive and conditionally probable events, let’s assume that the unit we work on admits only those patients with one of three mutually exclusive disorders: cryptogenic tinea pedis (CTP),8 idiopathic hangnail syndrome (IHS), and iatrogenic systemic decompensation (ISD). However, these conditions don’t occur with equal frequency; CTP is relatively rare, and only 10% of our patients suffer from this, as opposed to 30% from IHS and 60% from ISD. Moreover, the proportion of males and females is different for each disorder; these are given in the third column of Table 5–2.
Now, what is the probability that the next person through the door has either CTP or IHS? These are mutually exclusive events, so if the patient has one, he or she can’t have the other. Thus the probability is .10 plus .30; that is, there is a 40% probability that the person has either CTP or IHS, and, by extension, a 60% probability that he or she has ISD.
Why do we add the probabilities (rather than, say, multiplying them or taking their square roots)? It may help if we think for a moment in terms of bodies instead of proportions. If there were a total of 100 patients on our ward, 10 would have CTP, 30 would suffer from IHS, and 60 from ISD. So the condition would be satisfied (i.e., the next person through the door has either CTP or IHS) if he or she were 1 of the 10 from the first group or 1 of the 30 from the second; in other words, 40 of the 100 patients would satisfy the condition, and 60 would not. We can summarize what we’ve said by the additive rule:
If X and Y are mutually exclusive events, then the probability of X or Y is the probability of X plus the probability of Y.
For obvious reasons, this is called the additive law. Put into formal jargonese:
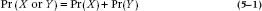
where “Pr” is statistical shorthand for probability. Needless to say, we’re not limited to just two events; the same law holds with as many mutually exclusive events as we want.
Conditionally Probable Events and the Multiplicative Law
Now, let’s change the question a bit. What’s the probability that the next patient will be a male and have ISD? These are not mutually exclusive events; a person with ISD can be either male or female. However, we know from experience that ISD is more common in males. This is a case of conditional probabilities because the probability that the patient has the diagnosis is conditional on the probability that the patient is a male (and vice versa). We know from Table 5–2 that 80% of patients with ISD are male, 50% of patients with CTP are male, and 30% of IHS patients are men. One way to answer this question is to redraw the table, giving the number of males and females with each of the diagnoses, as we’ve done in Table 5–3. We’ve based this on having 100 patients so that we’re working with whole numbers, but this will work with any number. We see that 48 of the 100 patients on our ward are males with ISD, so the answer is that there is a 48% chance that the next patient admitted to our ward will be a male and have ISD.
TABLE 5–2 Relative frequencies and gender differences for three disorders
| Disorder | Relative frequency | Male/female ratio |
| Cryptogenic tinea pedis | .10 | 50/50 |
| Idiopathic hangnail syndrome | .30 | 30/70 |
| Iatrogenic systemic degeneration | .60 | 80/20 |
TABLE 5–3 Actual number of patients with the three disorders
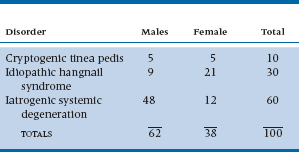
We can get at the answer another way, by looking only at the row and column labeled Total. In statistical parlance, we say that we’re looking at the marginals. The probability of having ISD is 60/100, or .60, whereas the probability of being a male, if the diagnosis ISD, is 48/60, or .80. So, the probability that both events occur together (i.e., a male with ISD) is .60 × .80, or 48%, which is exactly what we got before. We multiplied in this case because we’re looking at a part of a part. That is, some of the people are male (the others are female); and, looking at the patients from the other perspective, some of the total have ISD (the remainder have the other disorders). So, of the 60 patients who have ISD, 80% of them are male.
Using this technique of multiplying probabilities means that we can figure out the conditional probabilities by simply knowing the individual probabilities that certain events will happen, and we don’t have to make up a table such as Table 5–3. So this rule reads:
If X and Y are conditionally probable, then the probability that both will occur is the probability of X times the probability of Y, given X has occurred.
It goes without saying that this is referred to as the multiplicative law, which is written in statisticalese as:
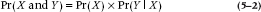
where the symbol Pr(Y | X) means the probability of Y given X; in our example, the probability of being a male, given that the patient has ISD. So, translating this equation from statistics into English, it reads, “The probability that the patient has ISD [X] and is a male [Y] is the probability of having ISD [Pr(X)] times the probability of being male, given that ISD is present [Pr(Y | X)].”
Just for practice, let’s run through a few other examples. The probability that the patient is a female with CTP is the probability of CTP (.10) times the probability of being female, given a diagnosis of CTP (.50), or 5%. The probability of a female with IHS is 21%; you figure it out for yourself.
Independent Events
Many events are neither mutually exclusive nor conditionally probable; they are independent of one another.9 A problem arises when events that are independent of one another are mistakenly assumed by some people to be conditional. Let’s say you’re back in the casino, standing over the roulette wheel. You’ve seen that the last five numbers have all been red. Now, you know that, assuming the wheel is honest, red and black have the same probability of appearing, so half the numbers should turn up red and half black. What’s the probability that the next number will be black?
The “gambler’s fallacy” is thinking that the sixth roll is conditional on the previous five, that after a long run of red the probability of a black is higher, so as to make the overall proportion of reds and blacks closer to 50%. However, the ball does not have a memory and has never studied probability theory; it doesn’t “know” what the previous results were, and the probability of black is 50% (ignoring the 0 and 00 slots for the moment), exactly what it would be if the previous five rolls had also been black. That is, the outcome is not conditional on the previous run; they are independent events. However, it’s been rumored that casino owners’ dreams are filled with fantasies of having a room full of people who believe in the gambler’s fallacy, rather than with images of girls from the chorus line.
Combinations and Permutations
As long as we’re in a casino, let’s see what other valuable lessons in life we can learn. If we’re playing stud poker, where five cards are dealt to each person, how many different hands can be dealt? For the first card, there are 52 possibilities. After this card is gone, there are then 51 possibilities left for the second card; then 50 for the third; 49 for the fourth; and 48 for the fifth. Thus, the total number of different hands is:
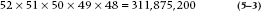
To make our life a bit easier, let’s define a few terms and symbols, and discuss the general rules:
n is the total number of “objects” in the set, which in this case is 52, the number of cards;
and
r is the number of objects that we’re looking for, which is 5.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


