Learning Outcomes
After completing this chapter, you will be able to
Explain why it is important to follow a standardized approach when using math in pharmacy.
Convert between different systems of measurement.
Perform and check key pharmacy calculations, including the calculations needed to interpret prescriptions and those involving patient-specific information.
Key Terms
| alligation method | A way to help determine how many parts of each strength should be mixed together to prepare the desired strength. |
| apothecary system | A system of measurement, originally developed in Greece for use by physicians and pharmacists but now largely replaced by the metric system, including the grain and the dram, the most common apothecary measures seen today. |
| avoirdupois system | A French system of mass that includes ounces and pounds; the system of mass most commonly utilized in the United States. |
| body mass index (BMI) | A measure of body fat based on height and weight, used to determine if a patient is underweight, of normal weight, overweight, or obese. |
| body surface area (BSA) | The total surface area of the body, taking the patient’s weight and height into account and expressed in m2. |
| days supply | The amount of medication dispensed for a specified time period. |
Metric System (International System of Units)
Converting Between Systems of Measurement
|
Pharmacy technicians and pharmacists in many settings use pharmacy calculations every day to determine, for example, the correct dose of a medication for a patient, the correct amount of ingredients to include in a compounded product, or the amount of medication a patient should receive. It is important to develop a systematic approach to solving pharmacy calculations that is reliable and consistent, with built-in checks along the way to ensure accuracy. Although it may seem as though completing a calculation two or three times is too time-consuming, it is time well spent when considering the potential for patient harm. Double-checking pharmacy calculations can lead to identification of abnormal doses, requests for early refills, incorrect quantities, or even incorrect medications. This chapter outlines the steps necessary to perform essential calculations and provides opportunities to apply the information to patient-specific scenarios.
Math Concepts
Most pharmacy calculations involve basic math. Numerals or numbers in different forms commonly appear on prescriptions and medication orders. Each of these basic math concepts is reviewed below.
Review of Basic Math
A numeral is a symbol, letter, or group of symbols or letters that represents a number. Common numerals in pharmacy calculations are Arabic numerals (e.g., 0, 1, 2) and Roman numerals (e.g., ss, I, V, X). Roman numerals are used in pharmacy only to designate a quantity on a prescription. Common Roman numerals in pharmacy include:
ss = 1/2 L or l = 50
I or i = 1 C or c = 100
V or v = 5 M or m = 1000
X or x = 10
When presented with a Roman numeral, it is important to pay attention to the order of the symbols. First, identify the largest Roman numeral. If more than one numeral of the same quantity is present, then add them together. Second, locate the smaller numerals. If the smaller numerals are to the right of the largest numeral(s), the quantity of the small numerals is added to the largest numeral. If the smaller numerals are to the left of the largest numeral(s), the quantity of the smaller numerals is subtracted from the largest numeral(s).
Example: XXI = 10 + 10 + 1 = 21
Example: XIX = 10 + 10 – 1 = 19
Self-Assessment 14-1 Note: Answers to self-assessment questions can be found at the end of the chapter.
Convert Roman numerals to Arabic numerals:
a. iv
b. iii
c. xvi
d. MCX
e. cxx
A number is a numeral or a group of numerals. Examples of numbers are whole numbers (0, 1, 2), fractions (1/4, 2/3, 7/8), mixed numbers (1 1/4, 2 2/3, 10 1/2), and decimals (0.5, 1.5, 2.25).
Fractions
A fraction represents a part of a whole number. It is used to express quantities less than one or quantities between two whole numbers. A fraction is written as two whole numbers separated by a division line, for example, ¾. The number on top, or the numerator, represents the number of parts present. The number on the bottom, or the denominator, represents the total number of parts. Considering the simple fraction 3/4, 3 is the numerator and 4 is the denominator. Compound fractions or mixed numbers contain a whole number in addition to the fraction, such as 1 1/4. This can also be written as 1 + 1/4.
Fractions may be used in a variety of situations in pharmacy. For example, commonly used IV fluids include 1/2 NS (one-half normal saline) or 1/4 NS (one-quarter normal saline). Fractions appear when the prescriber intends to prescribe less than one unit of measure. For example, 3/4 teaspoon may be the prescribed volume of a medication dose for a child.
Fractions may lead to medication errors if someone mistakes the / for a 1. When using fractions, it is important to write clearly to avoid misinterpretation.
To simplify, or reduce, a fraction, find the greatest number that can divide into the numerator and denominator evenly. If you are not sure, begin with small numbers like 2 or 3. In the following example, both the numerator and denominator are divisible by 2. Fractions are usually represented in their simplest form.
| Example: Simplify the fraction 66/100. | |||
| 66 | divided by 2 | ==> | 33 |
| 100 | divided by 2 | ==> | 50 |
This fraction cannot be reduced further because no single number can be divided into both 33 and 50 evenly.
It is important to understand how to add, subtract, multiply, and divide fractions.
Adding Fractions
There are 3 simple steps to remember:
1. Make sure all the fractions have common denominators. The easiest way to do this is to enlarge the fraction by either multiplying both parts of the fraction by the denominator of the other or by using the lowest (or least) common denominator.
Example A: 3/4 + 2/3
3/4 * 3/3 = 9/12
2/3 * 4/4 = 8/12
In this case, the least common denominator is 12, since both denominators are divisible by 4.
Example B: 3/4 + 1/2
1/2 * 2/2 = 2/4
2. Add the numerators.
A: 9/12 + 8/12 = 17/12
B: 3/4 + 2/4 = 5/4
3. Reduce to the simplest fraction or mixed number.
A: 17/12 = 1 5/12
B: 5/4 = 1 1/4
Subtracting Fractions
The steps are similar to the steps followed for addition:
1. Make sure all fractions have common denominators.
Example: 1 7/8 – 1/2
In this example, the compound fraction, 1 7/8, needs to be converted to a simple fraction before we can find the common denominator. Remember, 1 7/8 is the same as 1 + 7/8, which is the same as writing 8/8 + 7/8, and 8/8 + 7/8 = 15/8. The number 2 goes into 8 evenly, so the common denominator of 1/2 and 15/8 is 8.
1/2 * 4/4 = 4/8
2. Subtract the numerators.
15/8 – 4/8 = 11/8
3. Simplify the fraction.
Because the numerator is greater than the denominator, we can simplify by removing the part of the numerator that is equivalent to the value of the denominator to equal one whole number, and continue doing this until the remaining numerator is less than the denominator. In this example, subtract 8 from the numerator to represent one whole number.
11/8 = 1 3/8
Multiplication
When multiplying fractions, it is not necessary to convert to common denominators. Steps to multiply fractions:
1. Multiply the numerators.
Example: 9/10 * 4/5
9 * 4 = 36
2. Multiply the denominators.
10 * 5 = 50
3. Express your answer as a fraction.
9/10 * 4/5 = 36/50
4. Simplify the fraction. In this example, both the numerator and denominator are divisible by 2.
36 divided by 2 = 18
50 divided by 2 = 25
Final answer = 18/25
Division
When dividing fractions, it is not necessary to convert to common denominators. Steps to divide fractions:
1. Convert the second fraction (divisor) to its reciprocal; that is, trade the places of the numerator and the denominator.
Example: 2/3 ÷ 1/3
1/3 is converted to 3/1.
2. Multiply the first fraction by the second fraction’s reciprocal.
2/3 * 3/1 = 6/3
3. Simplify the fraction.
| 6 | divided by | 3 = 2 |
| 3 | divided by | 3 = 1 |
| Final answer = 2 | ||
Self-Assessment 14-2
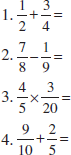
Decimals
Because fractions can be challenging to work with, some individuals prefer to convert them to decimals. Like fractions, decimals are also used to represent quantities less than one or quantities between two whole numbers. For example, 0.5 teaspoon means one-half of a teaspoon. Numbers to the left of the decimal point represent whole numbers, and numbers to the right of the decimal point represent quantities less than one (figure 14-1).
Medication errors can occur when decimals are used incorrectly or misinterpreted. Sloppy handwriting, stray pen marks, and poor quality faxed copies can lead to misinterpretation. Decimal point errors can lead to medication underdoses or overdoses. To avoid errors, healthcare professionals should follow a standardized approach to documenting decimals.
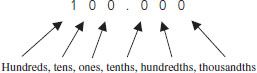
Figure 14–1. umbers to the left of the decimal point represent whole numbers, and numbers to the right of the decimal point represent quantities less than 1.
First, decimals should only be used when absolutely necessary. For example, five milligrams should be written as 5 mg, not 5.0 mg; the decimal point and trailing zero are not necessary. Use of a trailing zero in this example could cause the quantity to be misinterpreted as 50 mg. Second, only zeros serving as placeholders should be included after the decimal. For example, if you wish to write seven and five hundredths, it should be written as 7.05, with no zeros following the last significant digit (in this case, the 5). Third, a decimal point should not appear without a number before it. If you wish to write one-half milligram, it should be written as 0.5 mg, not .5 mg. This is referred to as proper use of a leading zero. Failure to use a leading zero in this example could lead someone to mistakenly read the quantity as 5 mg rather than 0.5 mg. Also, notice that there are no zeros following the 5, the last significant digit.
To prevent errors, remember to “always lead, never trail.” Use a leading zero when writing decimals that are less than 1 (e.g., 0.5 mg), and never use a trailing zero (e.g., 5.0 mg).
Pharmacy technicians need to know how to convert fractions to decimals. Using a calculator, divide the numerator by the denominator to obtain a decimal. If a whole number is present, that number is placed to the left of the decimal. For example, when converting 1 2/3 to a decimal, first place the 1 to the left of the decimal. Then divide the 2 by 3 to determine the numbers to the right of the decimal.
Example:
1 2/3 → place 1 to the left of the decimal: 1.xx
To determine the numbers to the right of the decimal, divide: 2/3 = 0.6667
Final answer = 1.6667
In most pharmacy calculations, decimals are rounded to tenths (most common), hundredths, or thousandths, depending on the situation. To round a number to hundredths, look at the number in the thousandths place. If it is 5 or larger, then you increase the hundredths value by 1. If the number in the thousandths place is less than 5, the number in the hundredths place stays the same. In either case, the number in the thousandths place is then dropped.
In the example above, if rounding to hundredths, the final answer is 1.67.
With respect to rounding, pharmacy numbers must be measureable and practical. For example, one would never see a dose of 4.324 mL of a medication. Depending on the medication, most milliliter (mL) measurements are rounded to the closest mL or tenth of a mL. Likewise, one would never see 4.1 teaspoons (which would typically be converted to mL anyway), 6.1 tablets, or 4.1 days. Table 14-1 includes examples of rounding.
Table 14–1. Examples of Rounding
| Number to be rounded | Round to tenths (look at the hundredths place) | Round to hundredths (look at the thousandths place) | Round to thousandths (look at the ten-thousandths place) |
| 1.515151 | 1.5 | 1.52 | 1.515 |
| 0.22222222 | 0.2 | 0.22 | 0.222 |
| 100.444445 | 100.4 | 100.44 | 100.444 |
| 4.56959 | 4.6 | 4.57 | 4.570 or 4.57 |
Self-Assessment 14-3
Convert the fractions to decimals, and round to the nearest hundredth:
a. 3/4 =
b. 2/5 =
c. 6/8 =
d. 9/16 =
e. 4/5 =
f. 2 3/8 =
g. 1/100 =
h. 7/8 =
i. 1 15/16 =
j. 3 7/8 =
To convert back to a fraction, write the decimal as the fraction you would say when you read the decimal. For example, 0.5 is read as “five tenths,” so write the fraction as = 5/10 Then simplify the fraction—in this case, to 1/2.
Percentages
Percentages are a blend of fractions and decimals. Because percentage means “per 100,” percentages can be converted to fractions by placing them over 100.
Example:
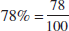
Percentages also convert simply to decimals. Just remove the % sign and move the decimal point two places to the left.
Example:
78% = 0.78
Self-Assessment 14-4
Express each percentage as a fraction and as a decimal.
| Percentage | Fraction | Decimal | |
| a. | 8% | 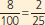 | 0.08 |
| b. | 67% | ||
| c. | 14% | ||
| d. | 92% | ||
| e. | 56.92% | ||
| f. | 0.05% |
Ratios and Proportions
A ratio shows the relationship between two items. For example, when calculating a dose, a ratio can be used to show the number of milligrams in the dose required for each kilogram of patient weight, which is written as mg/kg and read as “milligrams per kilogram.” Two ratios with the same units can be combined to create a proportion, or a statement of equality between two ratios. Write the units next to each number and double check that the units are lined up correctly (the same units appear on top of the equation and the same units appear on the bottom of the equation). If the units are mismatched, convert to matching units before solving.
When solving proportions, it is critically important to make sure the equation is set up correctly before you solve for the unknown variable (x in the following examples).
Example:
The standard dose of a medication is 4 mg per kg of patient weight. If the patient weighs 70 kg, what is the correct dose for this patient?
Set up a proportion to determine how many mg of the drug are needed for this patient:
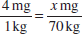
x represents the unknown value (in this case, the number of mg of drug in the dose) that you will find when you solve this problem. It takes two steps to solve for x:
Step 1: Cross-multiply.
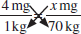
4 mg * 70 kg = 1 kg * x mg
Step 2: Divide both sides of the equation by 1 kg to isolate the unknown, x, on one side of the equation. Then you can solve for x.
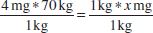
The kg units in the numerator and denominator cancel each other out, and any amount divided by one is equal to that amount.
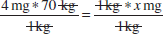
Therefore the equation becomes:
4 mg * 70 = x mg
x = 280 mg
Example:
Diphenhydramine 12.5 mg / 5 mL contains 12.5 mg per 5 mL. How many mg of diphenhydramine are in 10 mL of the solution?
Set up a proportion and solve for x.
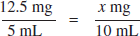
12.5 mg * 10 mL = x mg * 5 mL
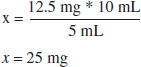
Self-Assessment 14-5
1. A solution of morphine sulfate contains 10 mg of active drug per 5 mL of solution. How many mg of drug are found in 30 mL of drug solution?
2. A suspension of sucralfate contains 1g of active drug per 10 mL of solution. How many mL are needed to obtain a dose of 575 mg for a child?
3. The usual dose of cefazolin for a child is 40 mg/kg. How many mg are needed for a 22-pound patient?
4. When cefuroxime powder for suspension is reconstituted, the final concentration is 125 mg/5 mL. How many mL of the solution are needed to obtain a 50-mg dose?
Systems of Measurement
Multiple systems of measurement are used in pharmacy. The most common system is the metric system, also known as the international system of units (SI). Pharmacy technicians and pharmacists need to know how to convert from this system to the apothecary, avoirdupois, and household systems.
Metric System (International System of Units)
The metric system is the most widely used and accepted system of measurement in the world. It is based on multiples of ten. The standard units used in healthcare are:
meter (distance)
liter (volume)
gram (mass)
The relationship among these units is: 1 mL of water occupies 1 cubic centimeter and weighs 1 gram.
There are prefixes that can be added to these standard measures to indicate a unit’s relationship to the standard unit. For example, “milli” means one thousandth; 1 milliliter is 1/1000 of a liter. Table 14-2 lists the common prefixes relevant to healthcare.
Oral solid medications are usually expressed in mg or g. Liquid medications are usually expressed in mL or L. If a dose or volume is not available commercially, the correct amount must be compounded or measured. Doing so may require converting between units of the metric system.
When filling medication orders, it is critically important that the technician pays careful attention to the units to prevent medication errors and potential patient harm.
Table 14–2. Commonly Used Metric Units and Prefixes, with Correct Abbreviations Relationship to standard unit
| Relationship to standard unit | 1/1,000,000 micro (mc)* | 1/1000 milli (m) | 1/100 centi (c) | Standard Unit | 1000 kilo (k) |
| Weight | microgram (mcg) | milligram (mg) | gram (g) | kilogram (kg) | |
| Volume | milliliter (mL) | liter (L) | |||
| Distance | millimeter (mm) | centimeter (cm) | meter (m) | kilometer (km) |
*Note that μ has been used as an abbreviation for micro, but this is an unsafe symbol because it can be confused with an “m.” The correct abbreviation for micro is mc.
In the metric system, each move of the decimal to the left or to the right in the number represents an increase or decrease in the magnitude of the unit. As long as you know the order of prefixes and the magnitude each represents, you can easily convert from one metric unit to another. The stem of the unit represents the type of measure. If you are converting to the left in Table 14-2, move the decimal to the right; your number will get bigger and your unit will get smaller. If you are converting to the right in the table, move the decimal to the left; your number will get smaller and your unit will get bigger. For example:
0.004 kg = 4 grams = 4000 mg
A kilogram is 1000 times as big as a gram. A gram is 1000 times as big as a milligram. A milligram is 1000 times as big as a microgram.
Example: sodium bicarbonate 650 mg tablets
1 tablet = 0.65 g = 650 mg = 650,000 mcg
Self-Assessment 14-6
Convert to the requested units:
| a. 42 mg = ___ g | b. 26 km = ___ m | c. 2 m = ___ mm |
| d. 84 L = ___ mL | e. 13.6 m = ___ mm | f. 0.4 L = ___ mL |
| g. 56 m = ___ cm | h. 43 kg = ___ g | i. 98.2 cm = ___ mm |
| j. 54 mg = ___ mcg | k. 96 mL = ___ L | l. 5.2 m = ___ cm |
| m. 0.87 mm = ___ m | n. 43.2 g = ___ kg | o. 32.5 mcg = ___ mg |
