[Note: This equation is the shortcut to the following:
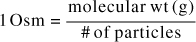
Then, this equation is converted to milliosmoles by dividing both sides by 1000, which yields the equation above. As a shortcut, then, the equation can be used remembering that in this instance, the unit of milligram is affixed to the molecular weight.]
This is very important—The molecular or atomic weights are usually assigned the unit of gram, however, for milliosmoles we assign the unit of milligram. The weight is not converted from gram to milligram. For example, if the molecular weight was given as 180 for an ingredient that dissociates into two ions, the value of 180 mg/2 would be the conversion factor.
Notice that instead of the valence as we saw in the denominator of the milliequivalent conversion, the number of particles generated by the disassociation of the ingredient is needed in the denominator of the milliosmole conversion.
When considering isotonic solutions, there is a “gold standard” of comparison. This is that 1 L of body fluid exerts 280 to 300 mOsm of osmotic pressure. So 1 L of any isotonic solution will exert 280 to 300 mOsm of osmotic pressure. Interestingly, the value of osmotic pressure is readily determined when manipulating either the concentration of particles in solution or the volume of solution.
If normal saline (0.9% sodium chloride) is isotonic, then 1 L of normal saline contains 280 to 300 mOsm of pressure. 500 mL of normal saline contains 140 to 150 mOsm (½ of the amount since 500 mL = ½ L). One liter of half strength saline (0.45% sodium chloride) would also contain 140 to 150 mOsm (½ the concentration, but still 1 L as the amount of fluid).
The other common solution that is isotonic is dextrose 5% in water. A liter of D5W contains 280 to 300 mOsm of osmotic pressure. The osmotic pressure of various concentrations and volumes can readily be determined.
Practice Exercises
Calculate the osmotic pressure:
1. 1 L of dextrose 10% in water
Answer
D10W is 2 times more concentrated than D5W, which is isotonic; therefore,
2 × 280-300 mOsm = 560-600 mOsm
2. 250 mL of dextrose 5% in water
Answer
250 mL = ¼ L, therefore ¼ × 280-300 mOsm = 70-75 mOsm
Answer
100 mL = 0.1 L, therefore 0.1 × 280-300 mOsm = 28-30 mOsm
Answer
2 L = 2 × 280-300 mOsm = 560-600 mOsm
Answer
D50 is 10 times 280-300 = 2800-3000 mOsm, but 50 mL is 1/20 of a liter then 1/20 × (2800-3000) = 140-150 mOsm
Answer
¼ × 280-300 mOsm = 70-75 mOsm
Answer
D35 is 7 times D5W and 500ml is ½ L
then ½ (7)(280-300 mOsm) = 980-1050 mOsm
Answer
½ × 280-300 mOsm × ½ volume = 70-75 mOsm
Answer
2 × 280-300 mOsm = 540-600 mOsm
Answer
250 mL = ½ L
then ¼ (280-300 mOsm) = 70-75 mOsm
Solve the Following Using the Conversion Factor Method
11. 1 L of dextrose 10% in water. MW = 180
Answer
1 mOsm = (180 mg/1 particle) = 180 mg (since dextrose does not dissociate)
10 g/100 mL = x/1000 mL x = 100 g
Convert to mg = 100,000 mg
100,000 mg/180 mg/mOsm = 555 mOsm
12. 250 mL of dextrose 5% in water. MW = 180
Answer
1 mOsm = (180 mg/1 particle) = 180 mg (since dextrose does not dissociate)
5 g/100 mL = x/250 mL x=12.5g
Convert to mg = 12,500 mg
12,500 mg/180 mg/mOsm = 69.4 mOsm
13. 100 mL of 0.9% sodium chloride solution (assume complete dissociation. MW = 58.5)
Answer
1 mOsm = (58.5 mg/2 particles) = 29.25 mg
0.9 g in 100 mL, convert to mg = 900 mg
900 mg/29.25 mg/mOsm = 30.8 mOsm
14. 2 L of normal saline (assume complete dissociation. MW = 58.5)
Answer
1 mOsm = (58.5 mg/2 particles) = 29.25 mg
0.9 g/100 mL = x/2000 mL
x = 18 g = 18,000 mg
18,000 mg/29.25 mg/mOsm = 615.4 mOsm
15. 50 mL of dextrose 50% MW = 180
Answer
1 mOsm = (180 mg/1 particle) = 180 mg
50 g/100 mL = x/50 mL
x = 25 g = 25,000 mg
25,000 mg/180 mg/mOsm = 138.9 mOsm
16. 1 L of 0.23% sodium chloride (assume complete dissociation. MW = 58.5)
< div class='tao-gold-member'>



